Построить плоскость параллельную прямой в кубе

Здесь рассмотрено подробное решение двух наиболее сложных, на мой взгляд, задач из представленных в группе Задачи на построение сечений многогранников на этом сайте. Если Вы еще не выполняли подобных заданий, вернитесь на указанную страницу и попробуйте поработать самостоятельно.

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

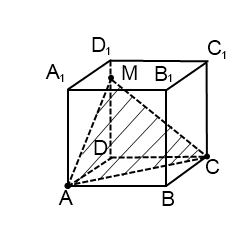
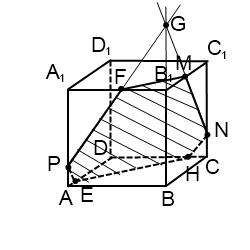
Задача 6.

Замечание: куб на чертеже может быть повёрнут к нам любой гранью, но трудно предугадать, какой удобнее для построения. Поэтому, если совсем не получается решение какой-либо задачи по стереометрии, то я рекомендую начинать заново, перерисовав исходный чертёж. А зачастую бывает достаточно просто переставить символы, обозначающие вершины основания многоугольника (естественно, не произвольно, а согласовав между собой и с условием задачи).

Для начала вспомним признак перпендикулярности прямой и плоскости.

Теорема. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, то она перпендикулярна плоскости.

Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Поэтому для реализации нашей цели нужно найти две различные плоскости, содержащие прямую B₁D, и построить в них нужные перпендикуляры. В качестве таковых в кубе можно взять, например, плоскости B₁BDD₁ и B₁ADC₁

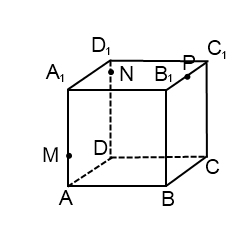
Построим сечение B₁BDD₁. Две противоположные стороны этого четырёхугольника являются рёбрами куба, а две другие — диагоналями его граней. По свойствам куба можем сделать вывод, что B₁BDD₁ – прямоугольник длина которого в √2 _ раз больше ширины. Делим диагональ на 4 части и ставим точку К, удовлетворяющую условию B₁K : B₁D = 1 : 4. Проводим через эту точку перпендикуляр к B₁D. Отрезок MN лежит на одной из искомых прямых.
При необходимости легко уточнить положение точек M и N на поверхности куба. Если задана длина ребра (или можно обозначить её, например, символом a), то длины отрезков B₁M и B₁N легко вычисляются из подобия прямоугольных треугольников, которое хорошо просматривается на плоском чертеже.

Получили четыре точки, принадлежащие искомой плоскости сечения и поверхности куба. Соединяем прямой линией точки M и F на грани BСС₁B₁. Соединяем точки F и N на грани A₁B₁С₁D₁ и продолжаем прямую до пересечения с ребром A₁B₁ в точке R. Соединяем точки R и E на грани A₁B₁BA и продолжаем прямую до пересечения с ребром B₁B в точке. M ? Но где гарантия, что именно в точке M, а не выше или ниже по ребру?

Если были проведены вычисления отрезков B₁F = B₁M и B₁N = B₁E в процессе анализа плоских прямоугольников, то ответ становится очевидным: так как прямоугольные треугольники B₁RF, B₁RM и B₁FM равнобедренные и равные.
Если же при построении положение точек M и F не вычислялось, а контролировался только факт их положения на рёбрах куба, то придётся произвести ряд вычислений на этапе доказательства верности построения.

Замечание I.
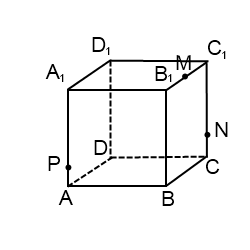
Возможен альтернативный подход к этой задаче. Так как куб является правильным многогранником и имеет центр симметрии, расположенный в точке пересечения диагоналей, а значит на линии B₁D, с которой мы работаем, то можно предположить, что сечение также будет симметричным и будет иметь форму равностороннего треугольника. Поэтому после анализа (жёлтого) прямоугольника на первом чертеже и получения точки М, можно сразу отложить от вершины B₁ на рёбрах куба равные отрезки B₁R = B₁F = B₁M, а затем доказать, что плоскость RMF перпендикулярна прямой B₁D. Для этого лучше всего воспользоваться теоремой о трёх перпендикулярах.

Теорема. Прямая, проведенная на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и самой наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Замечание II.
Вид сечения сильно зависит от положения точки K на диагонали куба. Попробуйте сместить точку K ближе к середине отрезка B₁D и построить MN ⊥ B₁D в прямоугольнике B₁BDD₁. На каких гранях и рёбрах куба теперь окажутся точки искомого сечения?

Ниже вы можете посмотреть маленькое видео о том, как изменяется сечение куба плоскостью, перпендикулярной его диагонали, в зависимости от положения их точки пересечения.

Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать

Задача 16.

При решении задачи предполагаем, что все операции на плоскости, в частности, построение параллельных и перпендикулярных прямых, нам известны из планиметрии и в подробном описании не нуждаются.

Решение.

Чтобы построить плоскость, параллельную заданной плоскости, нужно вспомнить признак параллельности двух плоскостей.

Теорема. Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости.

Теорема. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

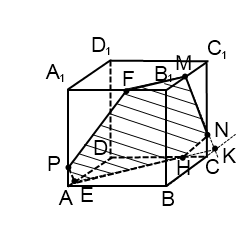
Кроме того, нам нужно, чтобы плоскость сечения проходила через заданную точку А₂. Значит, хорошо бы сразу найти две такие пересекающиеся прямые, параллельные каким-либо прямым в плоскости PQR, чтобы хотя бы одна из них содержала точку А₂. В этом и будет состоять первый этап решения задачи.

Через точки R и Р проводим РN || CC₁ и RM || CC₁ . Соединяем точки M и N прямой линией. По свойствам призмы получим MN || RР и MN = RР .

Терерь рассмотрим диагональное сечение призмы, проведенное через параллельные прямые AA₁ и СС₁. Плоскость AA₁C₁C содержит заданные точкии A₂ и Q и пересекает заданную плоскость PQR по линии QE. (Буквой Е обозначена общая точка линии пересечения плоскостей и прямой RP.) В этой плоскости (голубой на чертеже) через точку А₂ проводим прямую, параллельную QE до пересечения с верхним основанием призмы в точке F. А₂F || QE по построению.

На верхней грани призмы через точку F проводим прямую, параллельную линии MN, которая в нашем случае пересекает рёбра призмы A₁D₁ и B₁C₁ в точках H и G соответственно. HG || MN .
В зависимости от положения точки А₂ на ребре АА₁ положение точек H и G на рёбрах призмы может изменяться. Например, если бы точка А₂ располагалась ближе к вершине А₁, то точка G могла бы оказаться на ребре А₁В₁, а если бы она находилась близко к вершине А, то точка Н могла бы оказаться на ребре D₁С₁. От этого зависит окончательная форма искомого сечения призмы. Т.е. поскольку в условии задачи положение точек на рёбрах не фиксировано, то ваши ответы могут отличаться от приведенного мной не только формой на чертеже, но и количеством сторон получившегося многоугольника.

Обе прямые HG и RР параллельны прямой MN по построению, следовательно HG || RР . Для прямых в плоскости это вам уже известно давно. Для прямых в пространстве это тоже доказано.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Таким образом, прямые А₂F и HG и есть те самые прямые, которые мы искали. А₂F параллельна QE, следовательно параллельна плоскости PQR. HG параллельна RР, следовательно параллельна плоскости PQR. А₂F и HG пересекаются в точке F. Эти прямые определят секущую плоскость, параллельную заданной PQR.

Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Продолжим прямую HG до пересечения с ребром A₁B₁ в точке L. Точка L принадлежит верхней и фронтальной (на нашем чертеже) граням призмы, поскольку она принадлежит их общему ребру. Кроме того, точка L принадлежит плоскости сечения, поскольку находится на прямой HG. Следовательно, эта точка должна принадлежать и линии пересечения фронтальной грани с плоскостью сечения. Соединяем точку L с точкой А₂. Эта прямая будет принадлежать плоскости грани АА₁В₁В на основании следующей теоремы.

Теорема. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

Пользуясь этим же утверждением, соединяем и остальные две пары точек, принадлежащих одной грани призмы.

То, что оно удовлетворяет условию проходить через точку А₂ очевидно по построению. То, что плоскость A₂HGK параллельна плоскости RQP мы доказали, ссылаясь на соответствующие положения теории на каждом шаге построения.

Замечание.
Конечно, во время экзамена вы не будете делать несколько чертежей и так подробно описывать построение. Итоговый чертёж будет выглядеть примерно так.
Однако, не забывайте, что основное требование к заданиям второй части ЕГЭ профильного уровня это обоснованность решения. Поэтому, если вы просто выполнили все построения и представили на проверку итоговый чертёж, то к нему необходимо написать доказательство, которое содержит ссылки на теорию. При этом не обязательно цитировать теоремы полностью, можно упомянуть их названия.

Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.

Понравились материалы сайта?
Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Видео:Как строить сеченияСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

Сечение куба плоскостью

Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.

Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.

Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.

1) Построить сечение куба плоскостью, проходящей через точки A, C и M.

Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.

2) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.

Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).

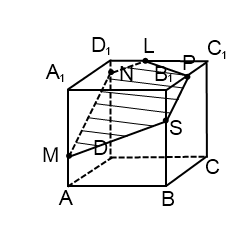
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).

Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.

Пятиугольник MNLPS — искомое сечение.

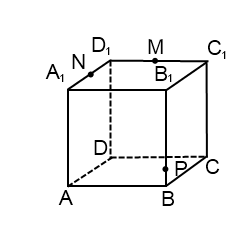
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).

Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.

Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).

Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.

Шестиугольник MNHEPF — искомое сечение.

Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.

Работа с прямой PE дает то же сечение MNHEPF.

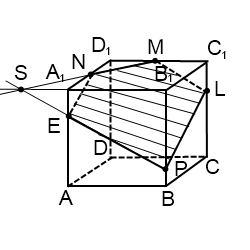
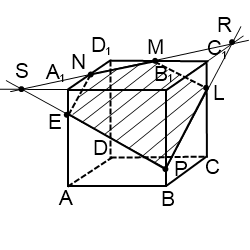
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.

Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.

Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.

Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Урок 3. Линейная перспектива. Построения, часть 1.

Без знания законов линейной перспективы невозможно реалистично изобразить ни один объемный предмет, будь то человек или табуретка.

Но пугаться не стоит. Несмотря на громкое название, основных законов всего два и запомнить их очень просто.

Все вы когда-нибудь ездили на электричке и переходя железнодорожные пути, смотрели не идет ли поезд. Что вы видели в этот момент?

Сходящие на линии горизонта рельсы, очевидно, параллельные друг другу.

И одинаковой высоты столбы линии электропередач, ближний из которых кажется значительно больше дальнего.

Собственно, это и есть два основных закона линейной перспективы:

1. Параллельные прямые, удаляющиеся от нас мы видим сходящимися в одной точке. Эта точка называется точкой схода. Она, или ее проекция находится на линии горизонта
2. Предметы одинаковой величины кажутся тем меньше, чем дальше от нас они расположены.

Видео:Построение сечения куба по трем точкамСкачать

Основные понятия перспективы.

Перед тем, как мы начнем применять эти законы на практике, я дам вам несколько определений. Это упростит объяснения и поможет вам легче понимать специальную литературу.

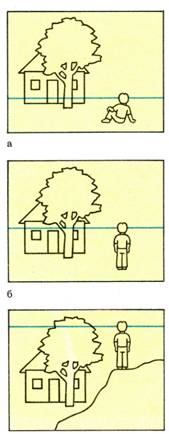
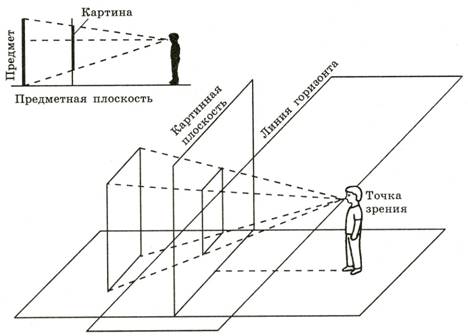
Горизонт ( линия горизонта) — плоскость, горизонтальная, бесконечная, находящаяся на высоте глаз наблюдателя и ВСЕГДА видимая в виде прямой горизонтальной линии.

Условно можно считать, что перспективный горизонт и горизонт географический в нашем зрении совпадают.

Все предметы, находящиеся ниже этой плоскости, ниже горизонта, мы видим сверху; все предметы, находящиеся выше горизонта,- видим снизу.

Важно запомнить, что линия горизонта всегда находится на уровне ваших глаз. Если вы сядете на землю, то перспективный горизонт опустится вместе с вами, при подъеме в гору он поднимается.

Точка зрения – условное расположение взгляда художника относительно изображаемого объекта.

Картинная плоскость — условная плоскость, на которую проецируется изображение. Она всегда вертикальна. Независимо от того, как расположен ваш лист.

Сокращения. Если поверхность находится под углом к картинной плоскости, она нам кажется более узкой, чем когда она параллельна картинной плоскости. Этот эффект называется — сокращения. Чем ближе угол между плоскостями к 90 градусам, тем больше сокращения. Если угол равен 90 градусам, мы видим поверхность, как линию.

Видео:Построение сечения параллельно прямойСкачать

Основные понятия. Тест.

Чтобы закрепить полученные знания, предлагаю вам пройти небольшой тест. Ответы присылайте, пожалуйста, мне в личном сообщении.

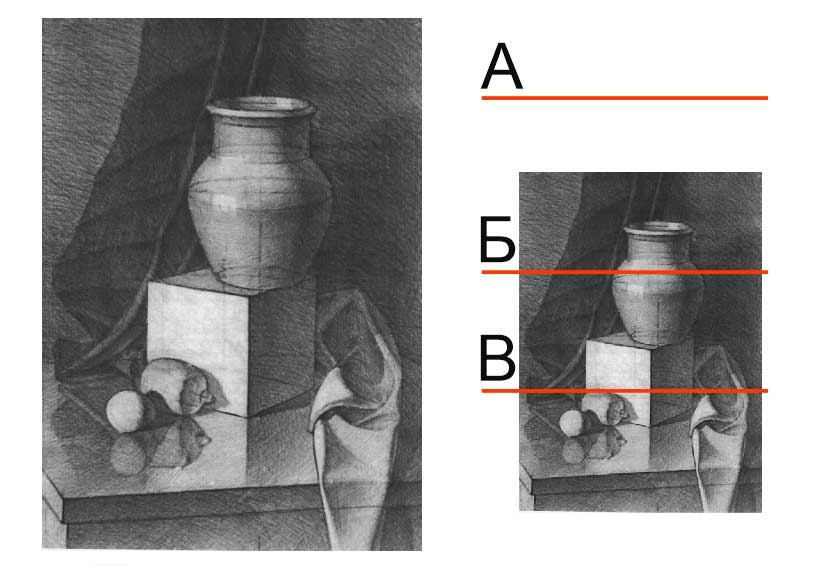
1. Где находится линия горизонта на картине.
   1. А
   2. Б
   3. В
   4. В натюрморте ее нет, горизонт виден только в пейзаже.
2. Картинная плоскость…
   1. … всегда совпадает с плоскостью листа, на котором вы работаете.
   2. … может совпадать, если лист расположен вертикально и прямо перед вами.
   3. … никогда не совпадает.
3. Геометрические тела в натюрморте находятся …
   1. … на линии горизонта.
   2. … выше линии горизонта.
   3. … ниже линии горизонта.
   4. … и выше и ниже.

Видео:Как строить сечения параллелепипедаСкачать

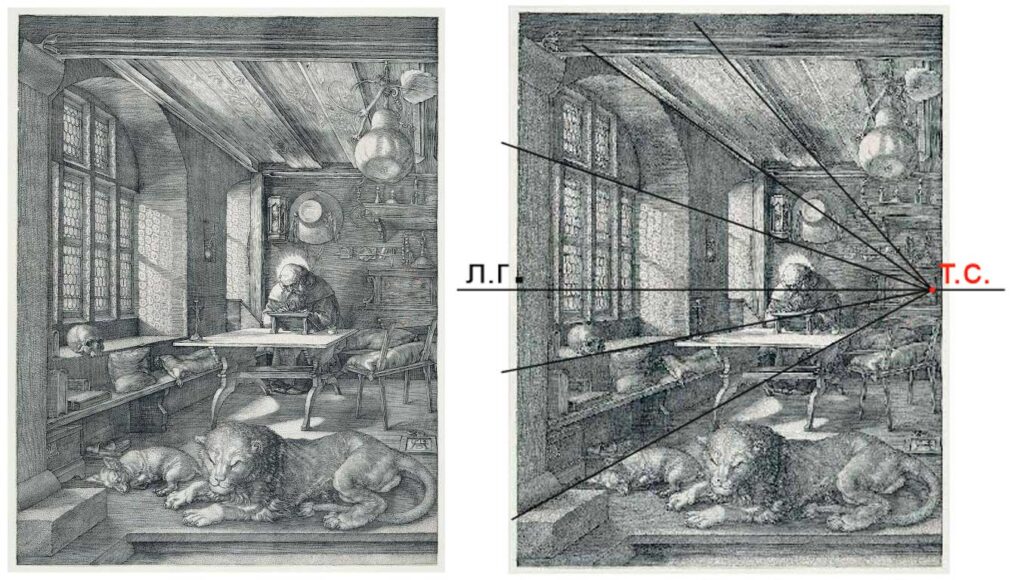
Перспектива с одной точкой схода.

Один из двух наиболее распространенных типов перспективных построений. Мы ее используем, когда рисуем объект с прямыми углами, передняя сторона которого параллельна картинной плоскости. Этот тип построений часто используется для изображений интерьеров и архитектуры.

Saint Jerome in His Study Albrecht Dürer 1514

Видео:ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

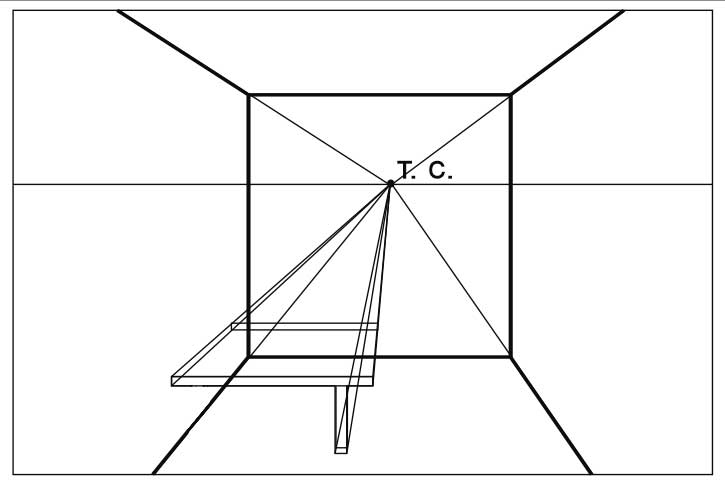
Разберем построения перспективы с одной точкой схода на примере построения куба.

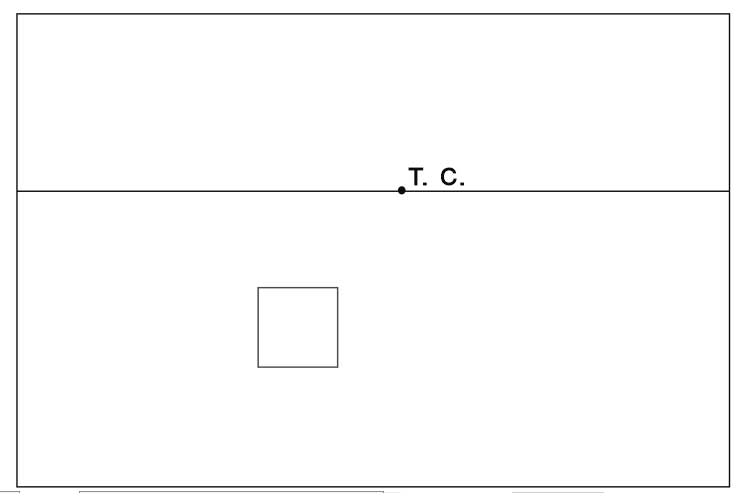
• Нарисуем на нашем листе линию горизонта. Местоположение выбираем произвольно, лучше в середине или верхней трети листаю
• Нарисуем переднюю сторону куба, ниже линии горизонта.Она будет видна нам без искажений, то есть как квадрат.

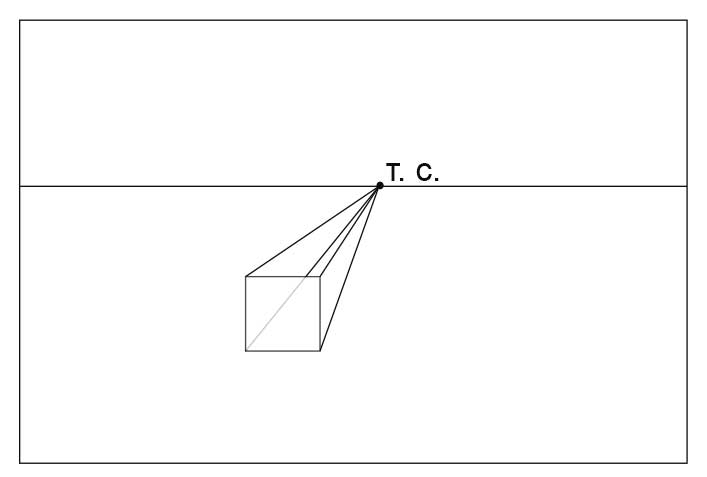
• Зададим точку схода (Т.С.) на линии горизонта. Когда мы рисуем по воображению, мы ее задаем произвольно. При натурном рисовании, она зависит от нашей точки зрения и определяется по параллельным прямым в изображаемом объекте.

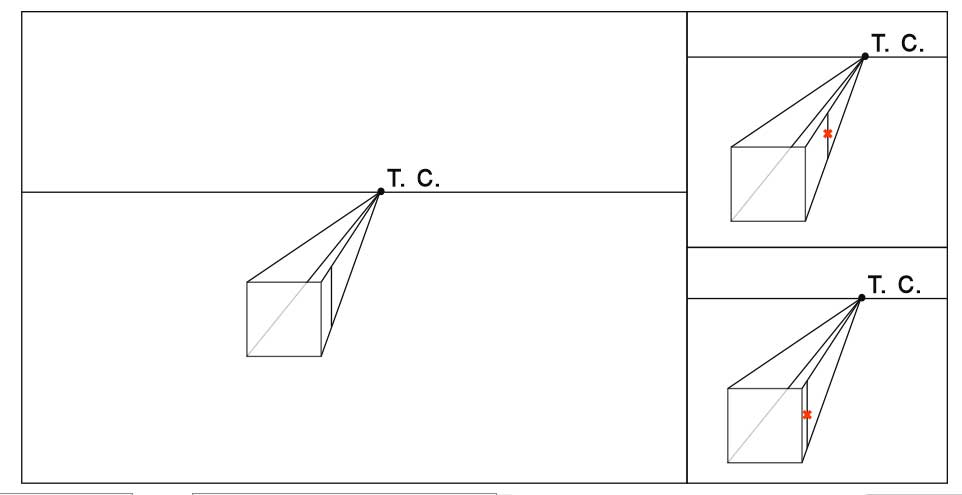
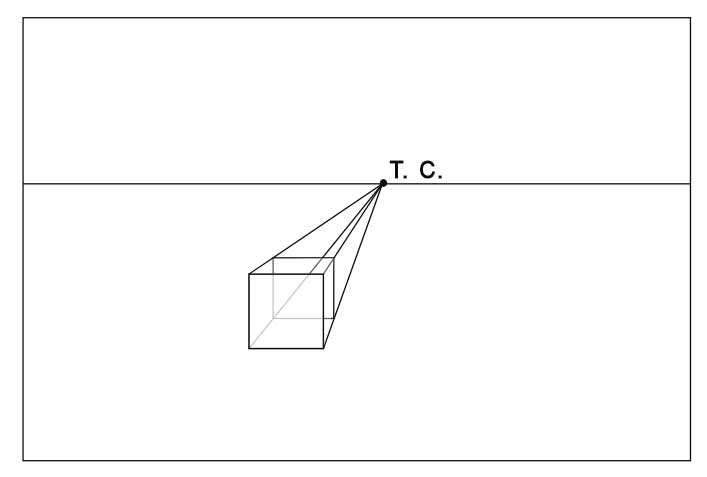
• Уходящие от нас ребра куба параллельны друг другу, а значит сходятся на линии горизонта в точке схода. Проведем прямые из углов передней стороны куба в точку схода.

• Определим на глаз длину уходящих от нас ребер куба. Мы видим их в сокращении. Справа от рисунка показаны ошибка при определении длины.

• Достраиваем дальнюю сторону куба. Обратите внимание, что она тоже видна нам без искажений, то есть, как квадрат.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

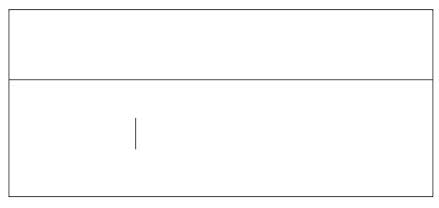
Упражнение 1.

Постройте кубы на линии горизонта и выше нее.

Видео:Параллельность прямой к плоскостиСкачать

Дополнительное упражнение 1.

Распечатайте работы, восстановите построение и найдите, где проходит линия горизонта.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

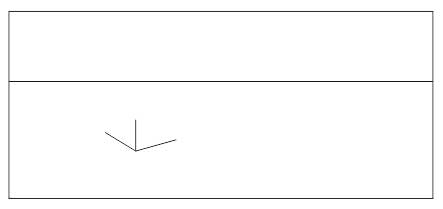
Дополнительное упражнение 2.

Постройте недостающие ножки у стола.

Видео:🔥Как строить сечения куба, параллелепипеда через заданные точки?Скачать

Перспектива с двумя точками схода.

Это более распространенный тип перспективных построений. Мы им пользуемся тогда, когда изображаем объекты, стороны которых расположены под прямым углом друг к другу. Сами эти объекты могут находиться под произвольными углом к картинной плоскости.

Обратите внимание, что несмотря на название типа построения, на одной работе точек схода может быть бесконечно много. Потому что для каждой группы параллельных прямых точка схода своя. Если у вас на работе несколько предметов, расположенных под разным углом к картинной плоскости, групп параллельных прямых тоже будет несколько.

View of Warsaw from the Terrace of the Royal Castle
Bernardo Bellotto1773

В одной работе могут совмещаться построение перспективы с одной и с двумя точками схода.

В системах построения с одной и с двумя точками схода мы условно считаем все вертикали строго вертикальны. Мы не учитываем, что вы смотрите на объект сверху или снизу и, соответственно, один из его краев ближе к вам, а вертикальные грани являются параллельными прямыми, удаляющимся от вас и должны иметь точку схода. Если вы хотите учитывать этот фактор, вам нужно использовать систему построения с тремя точками схода. Но о ней и о других системах построения объемных изображений мы будем говорить в следующем курсе.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

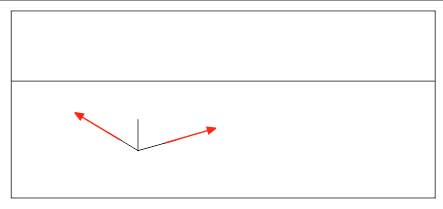
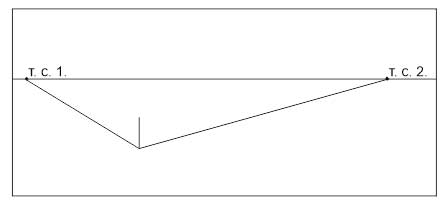
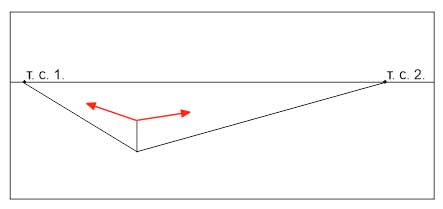
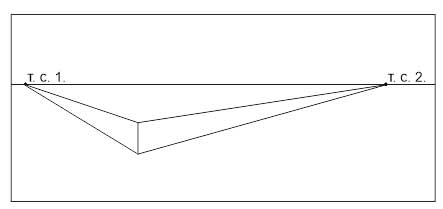
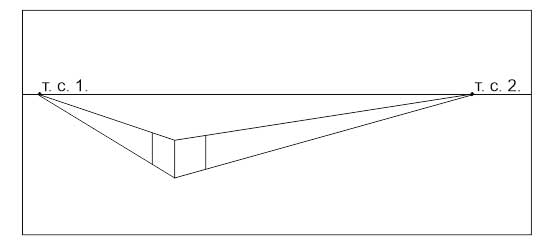
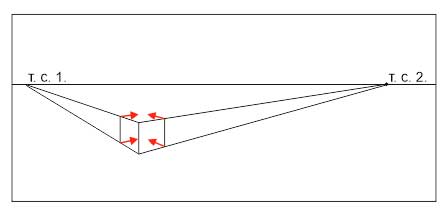
Разберем построения перспективы с двумя точками схода на примере куба.

• Проводим линию горизонта по центру листа или чуть выше.
• Произвольно задаем длину переднего вертикального ребра куба.

• Задаем направления горизонтальных, уходящих от нас, ребер куба. Углы выбираем произвольно, но стараемся, чтобы визуально угол между ребрами читался как прямой. (Он не будет прямым в геометрическом смысле, так как он находится не в плоскости, параллельной картинной, и мы видели его с перспективными искажениями)

• Продлеваем горизонтальные ребра до линии горизонта. На пересечении получаем две точки схода (Т.С1 и Т.С.2).

• От верхнего края переднего ребра проводим линии в точки схода.

• На глаз определяем ширину боковых сторон куба. Обратите внимание, что их ширина будет меньше высоты, так как мы видим ее в сокращении, а высоту- нет. Чем на вашем рисунке меньше угол между горизонтальным и вертикальным ребром, тем уже соответствующая сторона.

• От дальних углов боковых поверхностей проводим линии в точки схода.

• На пересечении получаем верх и низ дальнего вертикального ребра. Соединяем их — строем ребро.

Видео:Пересечение прямой и плоскостиСкачать

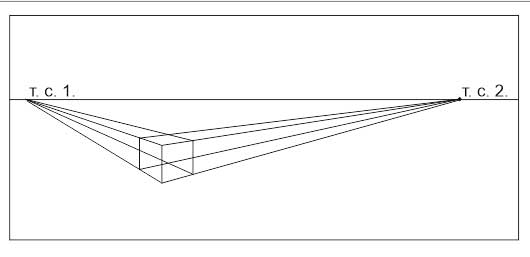
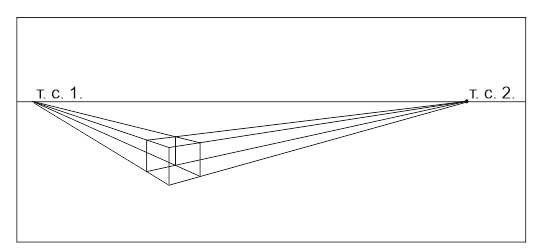
Упражнение 2.

Постройте кубы на и выше линии горизонта с теми же точками схода.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Задание. Воображаемый интерьер.

То, что окружает человека иногда говорит о нем больше, чем его внешность. Мне бы хотелось, чтобы вы придумали интерьер «с характером»: пространство, глядя на которое понимаешь, кто там обитает или что там произошло. Хотя ни обитателей ни событий мы не видим.

Как примеры тем предлагаю:

» комната, где прячется преступник»

«комната одинокого человека»

«комната, где находят ответы на вопросы»

Если вы боитесь не справиться с интерьером, можно взять упрощённый вариант задания — предмет мебели, по которому можно узнать владельца, Например: » любимое кресло старого профессора». Можно пофантазировать на тему любимых предметов мебели литературных героев.

Видео:Построение сечения кубаСкачать

Дополнительное упражнение 3.

Даже мастера путались в построениях.

Распечатайте картины, восстановите линии построения и найдите, где ошиблись художники.

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

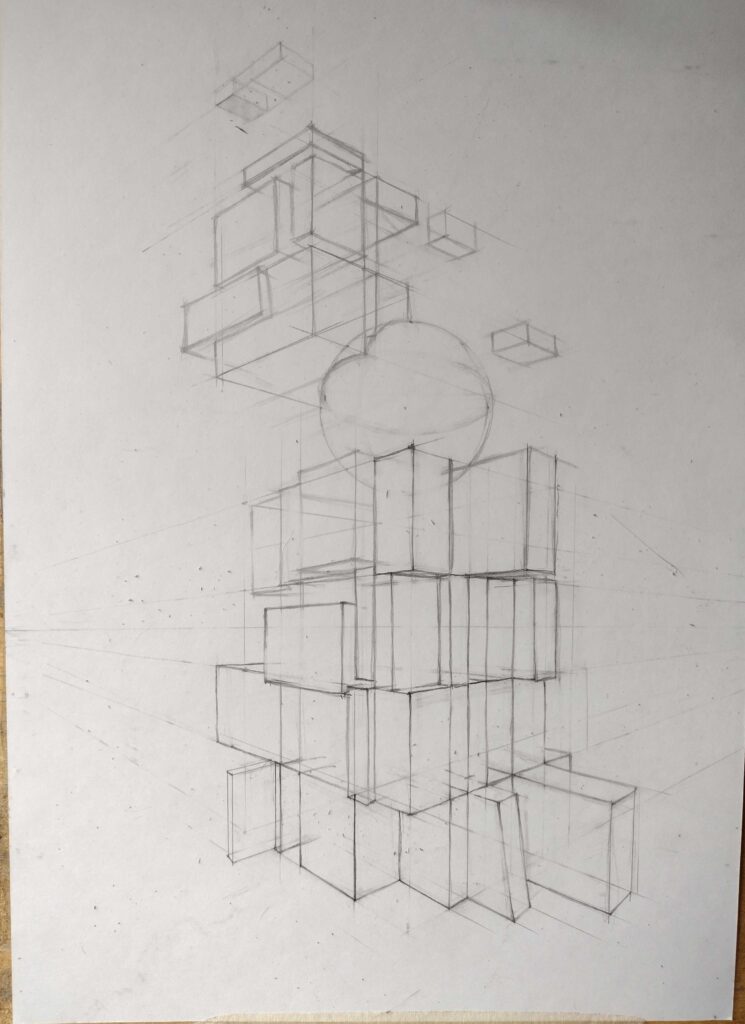
Дополнительное задание.

Композиция из геометрических тел. Линейный рисунок без тона. Основные элементы строим напросвет( так, как будто они из стекла) Стараемся пока использовать только кубы или прямоугольные параллелепипеды.

Кубы построены напросвет

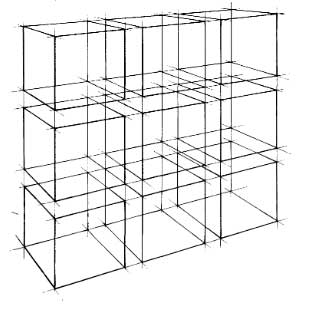
Предлагаю вам вообразить себя архитектором или скульптором-абстракционистом и придумать интересную и эстетичную конструкцию из геометрических тел. Вы можете создать просто гармоничную структуру или попробовать изобразить абстрактное понятие, например, тяжесть или легкость, величие, власть или угрозу. Любые, даже самые необычные варианты, приветствуются.

📹 Видео

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Построение сечений. Метод параллельных прямыхСкачать