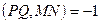Гармоническая четверка точек на окружности

Свойства полного четырехвершинника.

1. На каждой стороне полного четырехвершинника имеется гармоническая четверка точек: одна пара точек этой четверки – вершины, другая образована диагональной точкой и точкой пересечения этой стороны с диагональю, проходящей через две другие диагональные точки.

2. На каждой диагонали полного четырехвершинника имеется гармоническая четверка точек: одна пара точек этой четверки – диагональные точки, другая – точки пересечения сторон, проходящих через третью диагональную точку, с данной диагональю.

3. Через каждую диагональную точку полного четырехвершинника проходит гармоническая четверка прямых: одна пара прямых – две противоположные стороны, другая – две диагонали.

В силу свойств полного четырехвершинника построение четвертого гармонического элемента может быть выполнено проективными средствами, т.е. с помощью одной линейки.

Построение четвёртой гармонической точки к трем данным

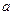
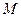
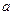
Задача №1. Пусть дана прямая и различные точки . Построить точку прямой , такую, что

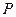
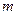
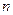
1. Проводим через точку две произвольные прямые и .

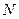
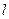
2. Через точку проводим произвольную прямую : .

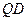
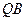
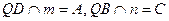
3. Проводим прямые и : .

4. Проводим прямую 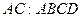— полный четырехвершинник.

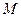
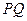
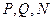
5. По свойству 2 точка пересечения стороны с диагональю является четвертой гармонической к точкам .

Задача №2. Построить четвертую гармоническую точку 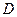к трем данным точкам на расширенной прямой.

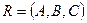
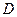
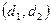
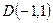
1. Возьмем на расширенной прямой репер . Пусть точка имеет координаты относительно данного репера. По свойству сложного отношения четырех точек имеем: и значит .

2. Построим точку 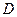по координатам относительно данного репера.

Дата добавления: 2017-01-29 ; просмотров: 2925 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:#30. Регион ВсОШ 2023, 10.5Скачать

Гармоническая четверка точек на окружности

Данное отношение направленных отрезков называют двойным отношением (cross-ratio) и обозначают ( AB, CD). Двойное отношение является инвариантом относительно любых проективных преобразований. В частности, если точки A, B, C, D, лежащие на прямой l, образовывали гармоническую четверку, то ее будут образовывать и точки A‘, B‘, C‘, D‘, являющиеся их проекциями на прямую p с центром в точке Р :

Соответственно, гармонической четверкой прямых, или гармоническим пучком прямых называют такие четыре прямые a, b, c, d, лежащие в проективной плоскости, и проходящие через одну общую точку Р, для которых любая четверка точек A ∈ a, B ∈ b, C ∈ c, D ∈ d, лежащих на одной прямой, является гармонической.

В частности, любые параллельные прямые каждого направления пересекаются в единственной бесконечно удаленной точке. Соответственно, противоположные стороны квадрата PQ , RS и прямая a пересекутся в некоторой бесконечно удаленной точке Y , а стороны PS , QR и прямая b — в некоторой другой точке X . Это и будут недостающие диагональные точки. Но самое важное здесь то, что эти точки также будут общими точками некоторых новых гармонических пучков прямых, которые в обычном евклидовом смысле нам были недоступны.

Рассмотрим внимательно бесконечно удаленную точку X . Как мы уже отмечали, она является общей для прямых b , PS и Q R. Но точки Х и Y однозначно определяют еще одну прямую — назовем ее условно h , поскольку, разумеется, она есть не что иное, как линия горизонта, в разных точках которого, собственно, и встречаются все параллельные прямые.

Видео:11. Инвариант - двойное отношение четырех точекСкачать

Элементы проективной геометрии (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

Теорема Паппа знаменита прежде всего тем, что это первая проективная теорема. Папп сформулировал и доказал ее примерно за полторы тысячи лет до возникновения проективной геометрии. При этом он не рассматривал ни проекций, ни сложных отношений.

Попробуйте сами доказать теорему Паппа, используя только теоремы школьного курса евклидовой геометрии. Нет сомнений, что на этом пути вас ожидают определенные трудности. Для этого, видимо, придется многократно применять к различным треугольникам теорему Менелая или теорему Чевы. Возможно есть и другие пути доказательства. Кто знает. Не зря же Папп был назван последним великим геометром античности.

Видео:Симедиана. Гармонические четырехугольники. | Олимпиадная математикаСкачать

Гармоническая четверка

Рассмотрим две пары точек, лежащих на одной прямой, таких, что (АВ, МР) = –1 или, другими словами, пары точек АВ и МР разделяют друг друга, и . Говорят, что точки А, В, М, Р образуют гармоническую четверку, или, что пары точек АВ и МР гармонически разделяют друг друга. Построим гармоническую четверку точек, пользуясь только центральной проекцией.

Точку М можно выбрать произвольно на прямой АВ, тогда положение точки Р однозначно определяется следующим построением.

Через произвольную точку К проведем прямые КА, КВ, КМ. На прямой КМ возьмем произвольную точку L. Прямые AL и BL пересекают прямые КА и КВ в точках А’ и В’. Прямая А’В’ пересекает АВ в искомой точке Р.

Действительно, (АВ, МР) = (А’В’,М’Р’), поскольку четверка точек А’В’,М’Р’ соответствует четверке АВ, МР при проекции с центром К.

Аналогично (А’В’,М’Р’) = (ВА, МР), так как четверке А’В’,М’Р’ при проекции с центром L соответствует четверка ВА, МР.

(АВ, МР) = (ВА, МР), то есть и, при этом пары точек АВ и МР разделяют друг друга. Это и означает, что пары точек А, В и М, Р (а вместе с ними и А’, В’ и М’, Р) образуют гармоническую четверку. Заметим, что положение точки Р на прямой АВ определяется только точками А, В, М, и не зависит от выбора вспомогательных точек К и L.

Заметим, кстати, что если точка М – середина отрезка АВ, то АВ║ А’В’, а точка Р становится бесконечно удаленной.

Обычно приведенное построение описывают следующим образом:

Возьмем на проективной плоскости четыре точки общего положения и соединим их шестью прямыми – каждую с каждой. Получится конфигурация, которую называют полным четырехвершинником.

Шесть прямых дадут еще три новых точки пересечения в дополнение к уже имеющимся четырем. Соединим эти три точки еще тремя прямыми. Их называют диагоналями четырехвершинника. Каждая из диагоналей пересекает стороны четырехвершинника в четырех точках. И каждая из этих четверок – гармоническая.

Однако это еще не все. На каждой стороне исходного четырехвершинника также образуются гармонические четверки (почему?). Таким образом, на чертеже всего тринадцать точек, девять прямых, и девять гармонических четверок – по одной на каждой прямой.

Таким образом гармоническая четверка определена только через инцидентность точек и прямых, чисто проективным образом. Действительно, при любой центральной проекции одной плоскости на другую четырехвершинник останется четырехвершинником, а гармоническая четверка – гармонической четверкой.

Из доказательства следует, что если выбрать на прямой три любые точки и достроить этот чертеж до полного четырехвершинника, то положение четвертой точки определяется однозначно, независимо от того, какой именно четырехвершинник был построен. Интересно, что это можно доказать, опираясь лишь на теорему Дезарга, не используя сложных отношений.

Придется при этом применить теорему Дезарга по крайней мере три раза к трем парам трехвершинников, так что полученное доказательство будет немного длиннее. Однако таким образом можно определить гармоническую четверку, не только не привлекая понятия длины отрезка, но даже и отношения длин.

Правда, в доказательстве теоремы Дезарга было использовано то же самое сложное отношение, но этого можно избежать, если с самого начала строить проективную геометрию, как аксиоматическую теорию (где одной из аксиом будет являться утверждение, знакомое нам, как теорема Паппа), вообще не используя понятия евклидовой геометрии. Однако, такой путь изложения вряд ли подходит для первого знакомства. Исторически все обстояло наоборот.

Сначала проективная геометрия возникла, как продолжение классической геометрии Евклида. Потом – в конце XIX века в работах Штейнера и Штаудта она была изложена, как независимая теория со своей системой аксиом, отличающихся от аксиом евклидовой геометрии. И, наконец, в начале ХХ века Кэли и Клейн из материала проективной геометрии построили евклидову и неевклидовы геометрии. Однако подробный рассказ об этом уводит далеко за рамки статьи.

Видео:Вписанная окружность и три точки на одной прямой | Готовимся ко ВсероссуСкачать

Гармоническая четверка (продолжение)

В предыдущей главе гармоническая четверка точек была построена одной линейкой, в духе проективной геометрии. Вернемся на привычную евклидову плоскость и проведем построение с использованием параллельности, равенства отрезков, углов, и прочих непроективных понятий. Впоследствии эти построения приведут к новым проективным теоремам.

Заметим во-первых, что если точка М – середина отрезка АВ, а точка Р – бесконечно удаленная, то АВ, МР – гармоническая четверка. Это произойдет, если одна из диагоналей четырехвершинника станет бесконечно удаленной прямой, а сам четырехвершинник будет выглядеть, как параллелограмм. Построив проекцию такой четверки на любую прямую, получим также гармоническую четверку.

Чтобы построить проекцию бесконечно удаленной точки Р, достаточно провести через центр проекции прямую, параллельную АВ.

Пусть на прямой АВ задана произвольная точка М. Проведем через точку В произвольную прямую и отложим на ней два равных отрезка ВМ’ и М’А’. Прямые АА и ММ’ пересекаются в точке О. Проводя через точку О прямую, параллельную М’А’, до пересечения с АВ в точке Р, получаем гармоническую четверку АВ, МР.

Действительно, четверка АВ, МР является проекцией гармонической четверки А’В, М’Р∞, где М’ – середина отрезка А’В, а Р∞ – бесконечно удаленная точка прямой А’В.

Однако, гораздо более важные следствия можно получить из другого построения, известного еще Аполлонию.

Проведем в треугольнике АВС биссектрису угла С и перпендикулярную к ней биссектрису угла, внешнего к С. Эти биссектрисы пересекают прямую АВ в точках Р и М. По известной теореме планиметрии и . Следовательно, и АВ, МР – гармоническая четверка.

Угол между биссектрисами СР и СМ – прямой, значит точка С лежит на окружности с диаметром МР (окружность Аполлония). Оказывается, если двигать точку С по этой окружности, то СР и СМ все время будут оставаться внутренней и внешней биссектрисами угла С в треугольнике АВС. Докажем это, а заодно получим еще один способ построения гармонической четверки с помощью окружности.

Для доказательства заметим, что прямые СА и СВ вторично пересекают окружность Аполлония в точках, симметричных относительно диаметра МР. Это следует из того, что равные вписанные углы при вершине С опираются на равные дуги PD и PE.

Наоборот, пусть А – произвольная точка на прямой, содержащей диаметр МР(точка А может лежать и снаружи окружности). Проведем через нее произвольную секущую CD и построим точку окружности Е, симметричную точке С относительно диаметра МР. Тогда прямая ЕС пересечет МР в точке В, и АВ, МР – гармоническая четверка. Действительно, СР и СМ будут являться внутренней и внешней биссектрисами угла С в треугольнике АВС в силу равенства соответствующих вписанных углов.

Интересно, что само построение возникает у Аполлония при решении такой задачи: найти геометрическое место точек плоскости, таких, что отношение расстояний от каждой из них до фиксированных точек А и В постоянно и равно k.

Две из этих точек – М и Р, гармонически разделяют данную пару А и В, а остальные лежат на окружности с диаметром МР. Это следует из свойства биссектрисы .

Можно также заметить, что если на чертеже точки С и Е совпадут, то прямая ВС станет касательной к окружности. Легко доказать, что и в этом случае СМ и СР останутся биссектрисами соответствующих углов. Треугольник АВС станет прямоугольным, тогда из подобия треугольников АСО и СВО следует:

или , где R – радиус окружности.

Если теперь рассмотреть прямую АВ, как ось координат с началом в точке О, то точки М, Р,А, В будут иметь координаты , или если положить R = 1, то получим .

Точки А и В, гармонически сопряженные относительно концов диаметра МР называются симметричными относительно окружности. Построить их можно также, проводя касательные к окружности, как это видно на чертеже.

Можно рассмотреть преобразование плоскости, которое обменивает местами симметричные точки. При этом все точки, находившиеся внутри окружности, оказываются снаружи, и наоборот. Это преобразование называется инверсией плоскости и обладает многими интересными свойствами, однако подробный разговор о нем – задача другой статьи.

Видео:#5str. Как проверять перпендикулярность?Скачать

Полюс и поляра

Рассмотрев точки, гармонически сопряженные относительно концов диаметра, естественно попытаться рассмотреть точки, гармонически сопряженные относительно концов произвольной хорды. Возьмем произвольную точку А внутри или снаружи окружности и проведем через нее все прямые, пересекающие окружность. Будем для каждой хорды МР строить точку В так, чтобы точки АВ, МР образовали гармоническую четверку.

Докажем, что геометрическое место точек В является некоторой прямой. Эта прямая называется полярой точки А. Для доказательства рассмотрим два случая: 1) точка А расположена вне окружности, 2) точка А расположена внутри окружности.

Интересно, что несмотря на различия между чертежами, текст доказательства практически не меняется.

Проведем через точку А диаметр и построим точку С, которая вместе с точкой А гармонически разделяет концы диаметра. Проведем через точку С перпендикуляр р к диаметру и покажем, что любая прямая, проходящая через точку А, пересекает этот перпендикуляр в такой точке В, а окружность в таких точках М, Р, что АВ, МР – гармоническая четверка.

По предыдущей задаче прямые МС и МА пересекают окружность в точках D и Р, симметричных относительно диаметра. Отсюда следует, что прямая СА является биссектрисой угла С в треугольнике МРС. В случае (1) – это внешний угол, в случае (2) – внутренний. Прямая р, перпендикулярная диаметру, является биссектрисой смежного угла. Биссектрисы СА и СВ пересекают основание треугольника СМР в точках А и В, следовательно, АВ, МР – гармоническая четверка.

Прямая р называется полярой точки А. Точка А называется полюсом прямой р. Если полюс лежит внутри окружности, то поляра не пересекает окружность, если полюс лежит вне окружности, то поляра пересекает окружность. Легко видеть, что если точка А лежит на окружности, то ее полярой будет касательная в точке А. Полярой центра окружности служит бесконечно удаленная прямая. Если поляра проходит через центр, то ее полюс – бесконечно удаленная точка.

На первый взгляд между чертежами (1) и (2) есть существенное различие. На чертеже (2) любая точка В прямой р обладает тем свойством, что пара точек АВ гармонически разделяется концами хорды МР. На чертеже (1) это верно только для тех точек прямой р, которые лежат внутри окружности. Для других точек прямой р окружность и прямая АВ вообще не пересекаются, и точки М и Р отсутствуют.

С точки зрения классической (школьной) геометрии естественно считать, что в случае (1) искомым геометрическим местом точек служит отрезок прямой р, находящийся внутри окружности, а в случае (2) – вся прямая р. Однако, мы будем считать, что и в том и другом случае полярой точки А является вся прямая р. К сожалению, оправдать эту точку зрения можно, только рассмотрев точки с комплексными координатами, что явно не удастся сделать в пределах статьи. (Для этого лучше написать учебник.)

Поскольку точки, симметричные относительно окружности, можно построить, проводя касательные, то касательные и поляры оказываются тесно связаны. В частности, если полюс лежит вне окружности, то для построения поляры достаточно провести пару касательных из полюса. Полярой будет прямая, проходящая через точки касания.

Видео:Двойные отношения | Олимпиадная математикаСкачать

Принцип двойственности для поляр

Рассмотрим две точки А и В, гармонически разделяющие концы хорды МР. Будем называть точки А и В сопряженными относительно окружности. Пусть прямые а и b – поляры точек А и В соответственно. Поляра точки А проходит через точку В, а поляра точки В проходит через точку А. Прямые а и b также будем называть сопряженными относительно окружности.

Может показаться, что уже доказана главная теорема о полярах:

Теорема (принцип двойственности)

Если поляра точки А проходит через точку В, то и поляра точки В проходит через точку А.

Увы, приведенное рассуждение нельзя считать доказательством. Дело в том, что прямая АВ может не пересекать окружность. В этом случае теорема также верна, но доказательство придется изменить.

Заметим, что поляра точки А проходит перпендикулярно прямой ОА через точку А’, симметричную точке А относительно окружности, то есть . Это верно независимо от того, где лежит точка А, внутри или снаружи окружности.

Пусть В – произвольная точка на поляре а. Проведем из точки А перпендикуляр b к прямой ОВ и покажем, что прямая b является полярой точки В. Для этого достаточно показать, что прямая b пересекает ОВ в точке В’, симметричной точке В относительно окружности, то есть что .

Это следует из подобия треугольников ОАВ’ и ОВА’.

Значит, прямая b, проходящая через точку А, является полярой точки В. Это доказательство сохраняет силу при любом расположении точек А и В относительно окружности.

Переведя полученный результат на «школьный язык», без использования полюсов и поляр, получаем две достаточно сложные задачи.

Пусть А и В – две точки вне окружности. AP, AQ, BM, BN – касательные.

Легко видеть, что в одном случае прямые PQ и MN являются полярами точек А и В, а в другом случае прямые АВ и MN являются полярами точек С и В. Таким образом перед нами просто иллюстрации к доказанной теореме. Попробуйте решить эти задачи, используя только факты, известные из школьного курса геометрии. Это возможно, хотя и не очень просто.

Видео:Математика для всех. Алексей Савватеев. Лекция 3.2. Гармонический рядСкачать

Полярное преобразование

Ранее было замечено, что в проективной геометрии в формулировках теорем можно менять местами точки и прямые, сохраняя отношение «инцидентности». То есть вместо слов «прямая, проходящая через точку» подставлять в текст теоремы слова «точка, лежащая на прямой» и т. п. При этом некоторые теоремы вообще не изменяются, а некоторые переходят в другие, двойственные теоремы.

Теперь можно указать геометрическое преобразование плоскости, которое точки переводит в прямые, а прямые – в точки. При этом прямой, соединяющей две точки, соответствует точка пересечения двух прямых.

Зафиксируем на плоскости произвольную окружность и рассмотрим преобразование, которое каждой точке ставит в соответствие ее поляру, и каждой прямой – ее полюс относительно данной окружности. Это так называемое полярное преобразование.

Действительно, если поляры точек А и В проходят через точку М, то поляра точки М проходит через точки А и В. Это и значит, что при полярном преобразовании прямая m, соединяющая точки А и В, переходит в точку М пересечения поляр а и b.

Если же прямая m проходит через центр окружности, то поляры точек А и В параллельны или, другими словами, прямые а и b пересекаются в бесконечно удаленной точке. Следовательно, полюсом прямой, проходящей через центр окружности является бесконечно удаленная точка.

Полярой центра окружности является бесконечно удаленная прямая. Таким образом каждой точке проективной плоскости соответствует единственная прямая, а каждой прямой – единственная точка, а отношение инцидентности сохраняется.

Однако, это еще не все. Ранее мы определяли сложное отношение четырех точек, лежащих на одной прямой и сложное отношение пучка прямых, проходящих через одну точку.

Для точек .

Для прямых .

Если прямые a, b, m, p проходят через точки А, В, М, Р, то (АВ, МР) = (ab, mp).

Оказывается, полярное преобразование сохраняет сложное отношение.

Если полюса А, В, М, Р лежат на одной прямой, то их поляры a, b, m, p проходят через одну точку и (АВ, МР) = (ab, mp).

Заметим, во-первых, что если точки А, В, М, Р лежат на одной прямой l, то их поляры a, b, m, p проходят через полюс L этой прямой.

Сложное отношение точек (АВ, МР) равно сложному отношению прямых (ОА ОВ, ОМ ОР), проходящих через точку О. Осталось заметить, что поляры a, b, m, p соответственно перпендикулярны прямым ОА, ОВ, ОМ, ОР и, следовательно, углы между полярами равны углам между этими прямыми.

Это и доказывает утверждение теоремы, поскольку сложное отношение четырех прямых выражается через синусы углов между ними.

Видео:#25. SPbMO-2022, Final round, 10.3Скачать

Конические сечения

Внимательный читатель мог заметить, что приведенное определение полярного преобразования проективной плоскости не является, мягко говоря, вполне корректным. Главную роль в этом «определении» играет окружность. Но для проективной плоскости не определены понятия расстояния между точками и угла между прямыми. Ведь при центральной проекции не сохраняются ни углы ни расстояния.

Значит все рассуждения и доказательства, в которых встречаются биссектрисы, перпендикуляры, окружности, не могут быть использованы в проективной геометрии. Все, что мы можем себе позволить – это сложные отношения точек и прямых, в частности, гармонические четверки. И, прежде всего, необходимо найти проективный аналог окружности.

Рассмотрим центральную проекцию окружности на плоскость. Пучок прямых, осуществляющих проекцию, образует коническую поверхность.

След, который образует эта коническая поверхность при пересечении с плоскостью и есть центральная проекция окружности. Из евклидовой геометрии известно, что конические сечения бывают трех различных типов: эллипс, парабола, гипербола.

С проективной точки зрения никакой разницы между ними нет. Различие состоит лишь во взаимном расположении конического сечения (или, как часто говорят «коники») и бесконечно удаленной прямой. Эллипсом назовем коническое сечение, пересекающее бесконечно удаленную прямую, параболой – коническое сечение, касающееся бесконечно удаленной прямой, и гиперболой – если оно пересекает бесконечно удаленную прямую. Асимптоты гиперболы – это касательные в бесконечно удаленных точках.

Поскольку бесконечно удаленная прямая ничем не отличается от любой другой прямой проективной плоскости, то и различия между эллипсом, параболой и гиперболой на проективной плоскости нет.

Теперь дадим определение поляры точки относительно произвольного конического сечения. Поскольку при любой проекции гармоническая четверка остается гармонической четверкой, определение не претерпит существенных изменений.

Возьмем произвольную точку А на проективной плоскости и проведем через нее все прямые, пересекающие коническое сечение. Будем для каждой хорды МР строить точку В так, чтобы точки АВ, МР образовали гармоническую четверку. Все такие точки лежат на одной прямой, которая называется полярой точки А относительно конического сечения. Действительно, при центральной проекции окружность переходит в коническое сечение, гармоническая четверка – в гармоническую четверку, прямая – в прямую.

Для построения поляры можно было бы использовать касательную к коническому сечению, по крайней мере в том случае, когда полюс лежит вне коники, но мы поступим наоборот. Используем независимое построение поляры для того, чтобы провести касательные к коническому сечению.

Видео:В чем удивительная красота гармонического ряда? // Vital MathСкачать

Построение поляры одной линейкой

Первое и главное построение гармонической четверки связано с полным четырехвершинником. Естественно, поэтому, попытаться связать с ним и построение поляры. Для этого достаточно рассмотреть четырехвершинник, вершины которого лежат на коническом сечении. Проводя три его диагонали, получаем требуемое построение.

Действительно, на каждой стороне четырехвершинника образовалось по гармонической четверке. Например, диагональ АВ пересекает стороны четырехвершинника в точках, которые вместе с точкой С гармонически разделяют концы двух хорд конического сечения. Значит, прямая АВ является полярой точки С. Аналогично, прямые АС и СВ – это поляры точек С и А.

Трехвершинник АВС называется автополярным трехвершинником конического сечения, так как каждая его сторона служит полярой противоположной вершины.

Полученный чертеж можно воспроизвести, начиная с одной из точек А, В или С. Достаточно провести через нее любые две прямые, которые пересекут конику в четырех точках, а потом достроить остальные стороны и диагонали четырехвершинника. Теперь мы можем построить поляру любой точки относительно любого конического сечения. Таким образом, если дана любая точка вне конического сечения, можно построить две касательные при помощи одной линейки.

Это построение с одинаковым успехом можно применять к параболе, гиперболе или эллипсу, и, в частности, к окружности. То что касательные к окружности действительно можно строить таким образом, опять таки представляет собой весьма сложную задачу из «классической» геометрии. Во всяком случае, античным геометрам это построение не было известно.

Часто из технических соображений используют немного другое построение, не выходящее далеко за пределы окружности (конического сечения).

Заметим также, что теперь все проективные свойства поляр и полярного преобразования можно считать доказанными для произвольного конического сечения на проективной плоскости. Если, например, известно, что на евклидовой плоскости полярное преобразование относительно окружности сохраняет сложное отношение, то построив центральную проекцию на любую другую плоскость, увидим, что окружность станет коникой, полюса и поляры останутся полюсами и полярами, а все сложные отношения сохранятся. Значит и утверждение теоремы останется верным.

Видео:Гармония четырехугольников (feat. МО из Школково)Скачать

Еще о вписанном четырехвершиннике

Тот же самый четырехвершинник, вписанный в окружность, приводит к разным интересным задачам.

Проводя три диагонали вписанного четырехвершинника ABCD, получаем автополярный трехвершинник PQR. Каждая его вершина является полюсом противоположной стороны. Значит, поляра PQ перпендикулярна прямой ОR, соединяющей полюс R и центр окружности O. Точно так же перпендикулярны прямые PR и OQ, а также QR и ОР. Исключая из формулировки полюса и поляры, получаем теорему Брокара.

Пусть точки A, B, C, D лежат на окружности, а пары прямых АВ и CD, ВС и AD, АС и BD пересекаются соответственно в точках Р, Q, R. Тогда высоты треугольника PQR пересекаются в центре окружности.

Конечно же можно (в принципе) доказать эту теорему без привлечения проективной геометрии, «школьными» методами. Попробуйте!

Вот еще одна теорема, которую легко получить, используя полюса и поляры. Возьмем на окружности (коническом сечении) четыре точки А, В, С, D. Пусть прямые АВ и CD пересекаются в точке S, а прямые АС и BD – в точке М. Как известно, поляра точки S проходит через точку М.

В то же время из принципа двойственности следует, что поляру точки S можно построить, соединив полюса Р и Q прямых АВ и CD. Эти полюса легко найти, как точки пересечения касательных в вершинах А, В и C, D. Значит, точки P, Q, M лежат на одной прямой.

Применяя это же построение к прямым AD и ВС, получаем следующую теорему:

Если вокруг окружности (конического сечения) описан четырехвершинник, то прямые, соединяющие точки касания противоложных сторон, и диагонали четырехвершинника пересекаются в одной точке.

Эту теорему, конечно же, возможно доказать обычным образом, используя подобие треугольников. Кроме того в дальнейшем будет доказана теорема Брианшона, для которой теорема об описанном четырехвершиннике является естественным частным случаем.

Попробуем теперь применить доказанные теоремы для исследования свойств гиперболы. Напомним, что гиперболой называется коническое сечение, пересекающее бесконечно удаленную прямую. Касательные в двух бесконечно удаленных точках называются асимптотами гиперболы.

На евклидовой плоскости гипербола и окружность – это две различные кривые второго порядка. С проективной точки зрения между ними нет никакой разницы. Они просто по-разному расположены по отношению к наблюдателю. Все проективные свойства окружности будут также и проективными свойствами гиперболы, параболы и эллипса.

Пусть асимптоты гиперболы пересекаются в точке Р, полюсе бесконечно удаленной прямой. Проведем касательную в произвольной точке М. Эта касательная пересекает поляру точки Р и две касательные, проведенные из точки Р, в точках А, В, К таких, что АВ, МК – гармоническая четверка (почему?). Это верно для любой точки Р, лежащей вне конического сечения.

Но если точка К является бесконечно удаленной, то точка М, как известно, будет серединой отрезка АВ. Получаем теорему:

Отрезок касательной к гиперболе, отсеченный асимптотами, делится точкой касания пополам.

Еще одно важное свойство гиперболы можно получить с помощью теоремы об описанном четырехвершиннике.

Рассмотрим четырехвершинник ABCD, сторонами которого являются две касательные и две асимптоты (тоже касательные). В силу доказанной теоремы, прямые АС и BD пересекаются в точке, лежащей на прямой, соединяющей точки касания гиперболы с прямыми AD и ВС, то есть в бесконечно удаленной точке.

Это означает, что прямые АС и BD параллельны. Следовательно, площади треугольников АВС и ADC равны, откуда следует равенство площадей треугольников АВР и СDР. Значит верна теорема:

Треугольник, образованный асимптотами гиперболы и произвольной касательной, имеет постоянную площадь.

Видео:Вебинар 20.01.2024 «Организм человека тонкие плотные и срединные тела»Скачать

Проективное определение конического сечения

Определение конического сечения как центральной проекции окружности не является, увы, вполне «проективным». Во-первых, в этом определении задействована окружность. Определение же окружности как множества точек равноудаленных от центра не относится к проективной геометрии. Во-вторых, возникает естественный вопрос: является ли центральная проекция конического сечения также коническим сечением?

Действительно, рассмотрим проекцию окружности на какую-либо плоскость. Эту проекцию мы назвали коническим сечением (коникой). Теперь построим проекцию этой коники на другую плоскость. Является ли новая проекция также коническим сечением? Или, точнее говоря, можно ли рассматривать ее как центральную проекцию какой-нибудь подходящей окружности?

Для того, чтобы дать утвердительный ответ на этот вопрос, вспомним другое определение окружности. Возьмем на евклидовой плоскости две произвольные точки А и В. Окружностью назовем геометрическое место точек М таких, что направленный (!) угол ÐАМВ является постоянным и равным a. Направленный угол понадобился, чтобы, во первых, не говорить про углы a и 180° – a, а во-вторых, чтобы не удвоить окружность.

Если теперь взять на окружности четыре точки A, B, C, D, то для любой точки М, лежащей на окружности, сложное отношение прямых (MA MB, MC MD) будет одним и тем же. Это следует из того, что вписанные углы, опирающиеся на одну дугу, равны, а сложное отношение четверки прямых выражается через синусы углов между ними.

Можно рассмотреть отображение пучка прямых, проходящих через точку М, на пучок прямых, проходящих через точку N. Соответственными прямыми будем считать те прямые, точка пересечения которых лежит на окружности. Это отображение является проективным, поскольку сложное отношение прямых сохраняется.

Теперь можно дать проективное определение конического сечения без использования окружности.

Рассмотрим на проективной плоскости два пучка прямых вместе с проективным отображением одного пучка на другой. Если отображение не является перспективным, то точки пересечения соответственных прямых двух пучков не лежат на одной прямой.

Оказывается, эти точки пересечения обязательно лежат на какой-нибудь конике. Более того, это можно считать ее определением. Назовем коникой множество точек пересечения соответствующих прямых двух пучков, между которыми установлено проективное соответствие.

Ясно, что данное определение включает в себя окружность, как частный случай и, кроме того совершенно очевидно, что центральная проекция коники снова является коникой, поскольку при проекции сложные отношения сохраняются.

Осталось показать, что это определение совпадает с исходным, а именно, каждая коника (в смысле нового определения) является центральной проекцией какой-либо подходящей окружности.

Заметим сначала, что поскольку в случае окружности отображение пучка на пучок попросту сохраняет углы между прямыми, то прямой, соединяющей вершины пучков, соответствует при отображении касательная к окружности. Если рассматривать общую прямую MN, как принадлежащую пучку с вершиной М, то ей соответствует касательная в точке N, и наоборот.

Таким образом, чтобы задать два пучка, порождающих окружность, нужно провести всего пять прямых. Разумеется, три прямые, проходящие через точку М, можно выбирать произвольным образом. Затем на одной из них выберем точку N и проведем через нее еще две прямые, так чтобы соответственные углы оказались равными (см. чертеж).

Получаем по три прямых в каждом пучке, поскольку прямая MN входит в оба пучка сразу. Этого как раз хватает, чтобы задать проективное отображение одного пучка на другой. Для любой прямой из одного пучка можно теперь построить ее образ в другом пучке.

Это уже было сделано ранее одним способом, когда отображение пучков было представлено в виде композиции двух перспективных отображений. Впоследствии мы рассмотрим и другой способ, хорошо работающий в данном конкретном случае.

Перейдем теперь к случаю произвольной коники. Рассмотрим проективное отображение пучка a с вершиной М на пучок b с вершиной N. Общую прямую MN назовем l. Если бы прямая l при отображении оставалась на месте, то по доказанной теореме точки пересечения соответственных прямых из двух пучков лежали бы на оси перспективы.

📽️ Видео

Равнозвенная ломаная и касательная к описанной окружности | Готовимся ко ВсероссуСкачать

#26. EGMO-2022, Problem 6Скачать

Парадокс Бертрана – что не так со случайностью // Vital MathСкачать

#7str. Как использовать инверсию?Скачать

#4str. Разговор про равнобокие (равносторонние, прямоугольные) гиперболы. Часть IСкачать

✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

Торсионные поля. Акимов А.Е. Технологии, опередившие времяСкачать

Геометрия и группы. Алексей Савватеев. Лекция 13.1. Двойное отношение четырех точекСкачать

Урок 327. Гармонические колебанияСкачать