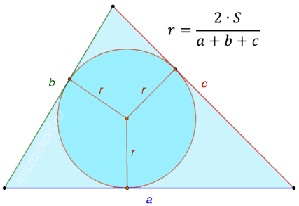
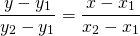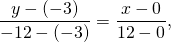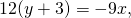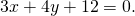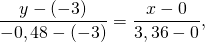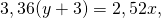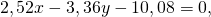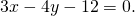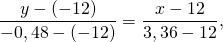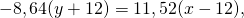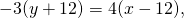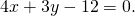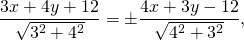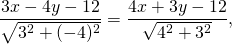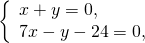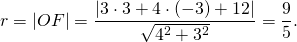Центр вписанной окружности по координатам вершин (6 видео)

Центр и радиус вписанной окружности в треугольник

Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника. Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.

Центр и радиус вписанной окружности в треугольник через координаты его вершин

Известны координаты вершин треугольника и известный координаты точки. Нужно установить принадлежность точки треугольнику.
Существует несколько способов определения. лежит-ли точка внутри треугольника или снаружи:

1. Метод сравнения площадей — по формуле Герона находятся площади 3-х треугольников которые образует точка с каждой стороной треугольника, далее находится площадь самого треугольника и сравнивается с суммой 3ех предыдущих треугольников, если суммы равны то значит точка принадлежит треугольнику.

2. Метод относительности — выбирается ориентация движения по вершинам треугольника, например по часовой стрелке. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Если точка для всех прямых, лежит с правой стороны, то значит точка принадлежит треугольнику, если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.

3. Метод геометрического луча — из точки пускается луч по какой-либо оси в каком-либо направлении. Вычисляется количество пересечений со сторонами, если кол-во нечётное, то значит точка лежит внутри многоугольника.

Содержание

Точка пересечения биссектрис
Окружность в треугольнике
Пример
Метод расчета центра окружности вписанного в треугольник
Шаг 1 :
Шаг 2 :
Шаг 3 :
Шаг 4 :
Шаг 5 :
🎦 Видео

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Точка пересечения биссектрис

Как найти точку пересечения биссектрис треугольника по координатам его вершин?

Как найти радиус вписанной в треугольник окружности по координатам его вершин?

Точка пересечения биссектрис треугольника является центром вписанной в этот треугольник окружности.

Эта точка равноудалена от сторон треугольника. Расстояние от точки пересечения биссектрис до сторон треугольника равно радиусу вписанной окружности.

Следовательно, все три задачи сводятся к нахождению точки пересечения биссектрис треугольника.

Для этого надо сначала составить уравнения биссектрис треугольника и найти точку их пересечения.

Дан треугольник ABC с вершинами в точках A(0;-3), B(12;-12) и C(3,36;-0,48).

1) Найти точку пересечения биссектрис треугольника ABC.

2) Найти радиус вписанной в треугольник ABC окружности.

3) Составить уравнение вписанной в треугольник ABC окружности.

1) Составим уравнения прямых, содержащих стороны треугольника.

Уравнение прямой AC:

Уравнение прямой BC:

Составим уравнение биссектрисы треугольника ABC, исходящей из угла B. Она образована прямыми AB и BC:

откуда уравнения биссектрис угла B: x-y-24=0 или x+y=0. Чтобы понять, которое из двух уравнений является биссектрисой внутреннего угла треугольника, следует подставить в уравнения координаты точек A и C. Поскольку они лежат по разные стороны от биссектрисы внутреннего угла B, то подстановка их координат в уравнение биссектрисы даёт числа разных знаков.

A(0;-3) и C(3,36;-0,48) в x-y-24=0: 0-(-3)-24 0. Получили числа разных знаков, x+y=0 — биссектриса угла B треугольника ABC.

Составим уравнение биссектрисы угла C. Угол C образован прямыми AC и BC, откуда

уравнения биссектрис угла C: 7x-y-24=0 и x+7y=0.

A(0;-3), B(12;-12) в 7x-y-24=0: 7·0-(-3)-24 0. Получили числа разных знаков, значит 7x-y-24=0 — уравнение биссектрисы внутреннего угла C.

Поскольку все три биссектрисы треугольника пересекаются в одной точке, третью биссектрису находить не требуется.

Точку пересечения биссектрис углов B и C найдём из системы уравнений

O(3;-3) — точка пересечения биссектрис треугольника ABC. Эта точка является центром вписанной в треугольник окружности.

2) Радиус вписанной в треугольник ABC окружности можно найти как расстояние от точки O до прямой AB, BC или AC. Найдем, например, расстояние от O до AB:

3) Чтобы найти уравнение вписанной в треугольник ABC окружности, в уравнение окружности подставляем координаты центра O(3;-3) и r=9/5:

Видео:Найти центр и радиус окружностиСкачать

Окружность в треугольнике

В каждый треугольник можно вписать окружность, притом только одну.
Центр вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.

Пример

В приведенном ниже примере, O является центров окружности.

Метод расчета центра окружности вписанного в треугольник

Даны точки вершин треугольника A(5,7), B(6,6) и C(2,-2). Итак, нам известны координаты точек вершин треугольника x1,y1, x2,y2 и x3,y3.
Для нахождения точки центра вписанной окружности необходимо найти уравнение биссектрисы.

Шаг 1 :

Давайте рассчитаем средние точки всех сторон треугольника AB, BC и CA заданных координатами x и y

Средняя точка стороны = x1+x2/2, y1+y2/2
Средняя точка AB = 5+6/2, 7+6/2 = (11/2, 13/2)
Средняя точка BC = 6+2/2, 6-2/2 = (4, 2)
Средняя точка CA = 2+5/2, -2+7/2 = (7/2, 5/2)

Шаг 2 :

Далее, найдем углы сторон AB, BC и CA используя формулу y2-y1/x2-x1. Пожалуйста, обратите внимание, что угол обозначается буквой ‘m’.

Угол AB (m) = 6-7/6-5 = -1.
Угол BC (m) = -2-6/2-6 = 2.
Угол CA (m) = 7+2/5-2 = 3.

Шаг 3 :

Теперь, давайте вычислить угол биссектрисы сторон AB, BC и CA.

Угол биссектрисы = -1/угол линии (стороны).
Угол биссектрисы стороны AB = -1/-1 = 1
Угол биссектрисы стороны BC = -1/2
Угол биссектрисы стороны CA = -1/3

Шаг 4 :

После того, как мы находим угол перпендикулярных линий, мы должны найти уравнение перпендикуляра, биссектрис с углом и серединой. Уравнение перпендикуляра АВ с серединами (11/2, 13/2) и углом 1.

Уравнение центра окружности y-y1 = m(x-x1)

Упростив, мы получим уравнение -x + y = 1

Кроме того, мы должны найти уравнение перпендикуляра, биссектрис линий BE и CF.

Для BC с средней точкой (4,2) и углом -1/2 y-2 = -1/2(x-4)

Упростив, мы получим уравнение x + 2y = 8

Для CA с средней точкой (7/2,5/2) и углом -1/3 y-5/2 = -1/3(x-7/2)

Упростив, мы получим уравнение x + 3y = 11