Радиус окружности основания цилиндра

В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.

Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

V = π R 2 h

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

S = 2 π Rh

3. Через полную площадь поверхности

Радиус цилиндра равен:

Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

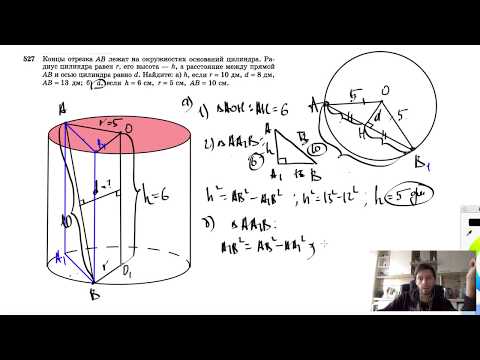
Видео:№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Видео:🔴 Радиус основания цилиндра равен 15, а его ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Рассчитайте радиус цилиндра

Круг (окружность) — геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).

Формулы для вычисления радиуса круга

Через объем и высоту $R=sqrt<frac>$, где:

V — объем цилиндра

h — высота цилиндра

Через площадь боковой поверхности и высоту $R=frac<S_>$, где:

S — площадь боковой поверхности

h — высота цилиндра

Через площадь полной поверхности и высоту $R=frac<sqrt<(2 pi h)^+8 pi S>-2 pi h>$, где:

Видео:Радиус и диаметрСкачать

Радиус цилиндра

При вращении прямоугольника вокруг своей стороны получается геометрическое тело, называемое цилиндром. Данная геометрическая фигура ограничена цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями — основаниями цилиндра. Радиусом считается отрезок, соединяющий на плоскости основания точку центральной оси цилиндра с точкой его поверхности.

— Если известен объем и высота цилиндра, можно найти его радиус, как корень квадратный из объема деленного на произведение числа пи на высоту цилиндра:

R = √V / πh

где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2 =πr (2h+r)

Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:

S (б.п.) = hP = 2πrh

— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:

r = S (б.п.) / 2πh

Площадь двух оснований равна удвоенному произведению пи на радиус в квадрате:

2S (осн.) = πr 2

— Если известна площадь основания и высота, радиус находим как корень квадратный из площади одного основания деленного на пи:

r = √S (осн.) / π

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2

где S (п.п.) — полная площадь поверхности цилиндра; r — радиус; h — высота.

🌟 Видео

Объём цилиндраСкачать

№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать

Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

ЕГЭ БАЗА 16 номер Радиус основания цилиндра равен 15, а его образующая равна 14Скачать

Видеоурок по математике "Цилиндр"Скачать

№534. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120Скачать

11 кл.Егэ. Радиус основания цилиндра равен ,2 высота равна 3 .Найдите площадь боковой поверхности циСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

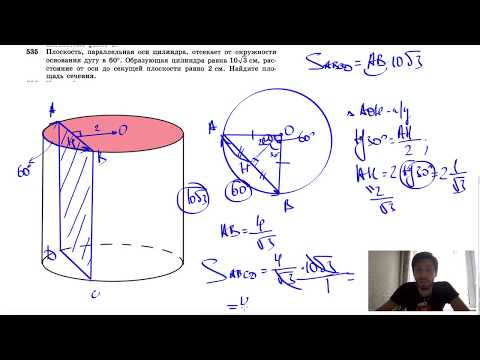
№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать

Длина окружности. Математика 6 класс.Скачать

Радиус описанной окружностиСкачать

Цилиндр - расчёт площади, объёма.Скачать

Найти радиус основания цилиндраСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Радиус основания цилиндра равен 26. Найти площадь сеченияСкачать

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндраСкачать