Как построить проекцию равностороннего треугольника (7 видео)

Построить проекции равностороннего треугольника

построить проекции равностороннего треугольника abc со стороной bc на прямой mn: a(105,50,25), m(15,100,70), n(155,100,110)

Содержание

Комментарии
Решения задачи
Начертательная геометрия Лекции, примеры выполнения задания
Построение аксонометрических проекций плоских фигур и гранных тел
📺 Видео

Решения задачи

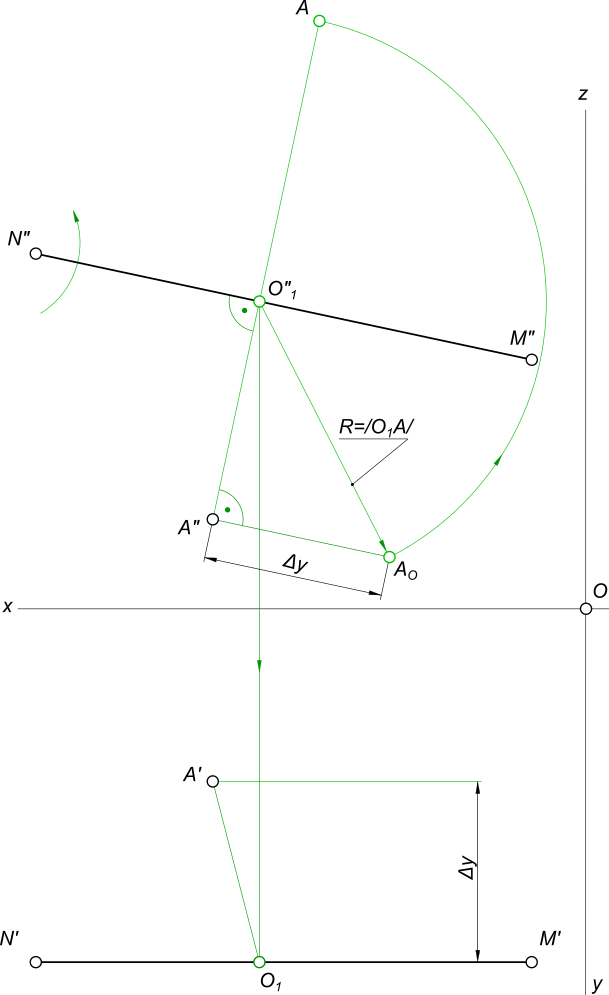
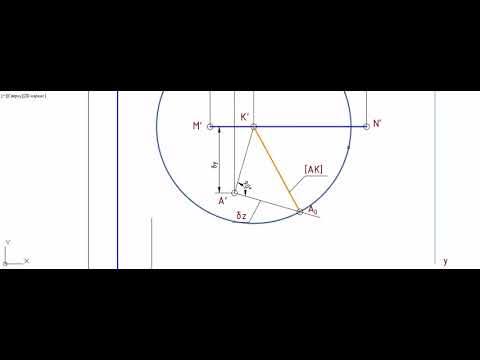
Построить проекции равностороннего треугольника ABC со стороной BC на прямой MN: A(105,50,25), M(15,100,70), N(155,100,110)

Построение проекций равностороннего треугольника

По заданным координатам построим проекции точки A и прямой MN Анализируем условие задачи: — прямая MN представляет собой фронтальную прямую (M’N’ // Ox); — треугольник равносторонний (его углы равны между собой и каждый равен 60°); — сторона BC лежит на прямой MN. Вырабатываем план решения задачи: — найти натуральную величину треугольника применив один из способов преобразования чертежа; — построить искомые проекции треугольника.

Видео:ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЛЬНИКА НА П1/П2 и углы наклона его плоскости к плоскостям проекцийСкачать

Начертательная геометрия Лекции, примеры выполнения задания

Задача: Построить проекции равностороннего треугольника АВС, принадлежащего плоскости Г(h Ç f), если его сторона АВ задана (рис. 4-56).

1. Чтобы построить проекции треугольника АВС, необходимо сначала определить его истинный вид. В этом случае решающим положением оригинала ( D АВС) является то, при котором плоскость треугольника параллельна плоскости проекций. Для этого плоскость Г(h Ç f) нужно поставить в положение плоскости уровня.

2. Чтобы плоскость Г поставить в положение плоскости уровня, требуется решить четвёртую задачу преобразования комплексного чертежа. Выбираем способ замены плоскостей проекций. Для решения четвёртой задачи требуется выполнить две замены.

3. Фиксируем систему П1 –П2, то есть, проводим х12 (рис. 4-57).

4. Меняем П2 на П4.

П4 ^ П1; П4 ^ Г ; П4 ^ h Þ x14h1

Так как плоскость Г на П4 спроецируется в прямую линию, то для её построения требуется всего 2 точки: Расстояние х1414 = х1212, х14А4 = х12А2. Г4 — главная проекция.

5. Меняем П1 на П5.

П5 ^ П4; П || Г Þ x45 || Г

Расстояние х4515 = х1411, х45А5 = х14А1.

6. В системе П4 – П5 плоскость Г — плоскость уровня, поэтому отрезок А5В5 — натуральная величина АВ, и треугольник АВС спроецируется на П5 в натуральную величину. Для его построения из точек А5 и В5 откладываем отрезки, равные А5В5, и получаем точку С5. Проекция А5В5С5 — натуральная величина равностороннего треугольника АВС.

7. Возвращаем точку С в систему П1 – П2 в обратном порядке (рис. 4-58).

Сначала находим С4 на Г4, проведя линию связи от С5 перпендикулярно х45.

8. От С4 проводим линию связи в системе П1 – П4 и откладываем расстояние х14С1 = х45С5.

9. От С1 проводим линию связи в системе П1 – П2 и откладываем расстояние х12С2 = х14С4.

10. Мы построили проекции равностороннего D АВС, принадлежащего плоскости Г(h Ç f).

Общая схема решения показана на рис. 4-59:

Задача: Определить расстояние между прямыми а и b (рис. 4-60).

1. В данной задаче параллельными прямыми а и b задана горизонтально проецирующая плоскость S (а || b). Чтобы расстояние между прямыми оказалось на чертеже в натуральную величину, решающим положением оригинала является такое, при котором плоскость S стала бы плоскостью уровня. Для этого необходимо решить четвёртую задачу преобразования комплексного чертежа.

2. Для преобразования выбираем способ вращения вокруг проецирующей оси. Так как плоскость S проецирующая, то для достижения цели достаточно одного вращения.

3. Выбираем ось вращения i так, чтобы она была горизонтально проецирующей (рис. 4-61а).

4. Радиус вращения R = i111

5. Вращаем проекцию плоскости S вокруг оси i1 до момента, когда она станет перпендикулярной линиям связи, и займёт положение S 1′ (рис. 4-61б).

6. Фронтальные проекции точек 12 и 22 совершат движение вправо по прямым, перпендикулярным линиям связи, и займут положение 12′ и 22′.

7. Прямые а2′ и b2′ — прямые уровня и расстояние между ними КР — натуральная величина расстояния между прямыми а и b (рис. 4-61в).

8. Возвращаем расстояние на П2 в обратном порядке (рис. 4-61г) — получаем К2Р2.

Видео:Построение равнобедренного треугольникаСкачать

Построение аксонометрических проекций плоских фигур и гранных тел

Построение аксонометрических проекций равностороннего треугольника:

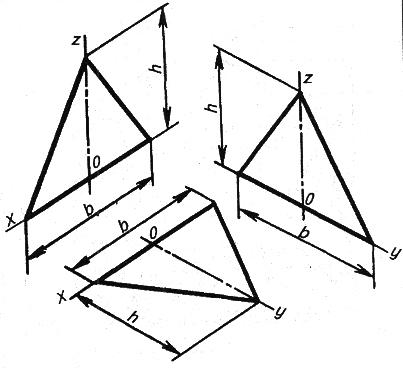
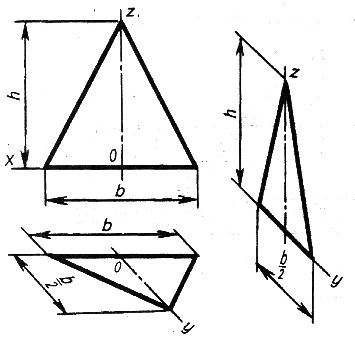
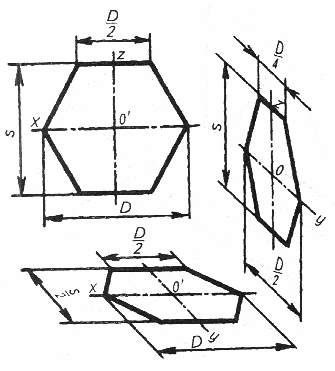
1. Треугольник расположен во фронтальной плоскости. По оси x откладываем по обе стороны от точки О отрезки b/2, равные в сумме b – стороне треугольника, а по оси z – его высоту h. Полученные точки соединяем отрезками прямых (рис.7,8).

2. Треугольник расположен в горизонтальной плоскости. По оси x откладываем от точки О отрезки b/2, равные в сумме b – стороне треугольника, а по оси y – его высоту h. Для изометрической проекции (рис.7) и половину его высоты

(h /2 ) – для фронтальной диметрии (рис.8). Полученные точки соединяем отрезками прямых.

3. Треугольник расположен в профильной плоскости. По оси y откладываем половину стороны (b/2) для фронтальной диметрической проекции и сторону b для изометрической, а по оси z – его высоту h (рис.7,8).

Построение аксонометрических проекций правильного шестиугольника:

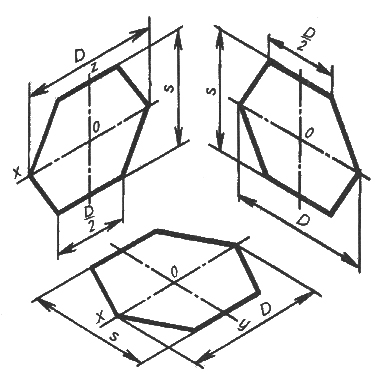
1. Шестиугольник расположен во фронтальной плоскости. По оси х, симметрично точке О откладываем радиусы описанной окружности вокруг шестиугольника (D/2), равные размеру стороны шестиугольника, а по оси z, также симметрично точке О – отрезки S/2, равные половине расстояния между противоположными сторонами шестиугольника. Через точки, полученные на оси z, проводим прямые, параллельные оси х, и симметрично оси z откладываем на них отрезки, равные половине стороны шестиугольника (D/2). Полученные шесть точек соединяем отрезками прямых (рис.9,10).

2. Шестиугольник расположен в горизонтальной плоскости. Построение выполняем, как было рассмотрено выше , с той лишь разницей, что расстояние S

( для изометрии, рис.9) между противоположными сторонами (для фронтальной диметрии S/2, рис.10) откладываем по оси y.

3. Шестиугольник расположен в профильной плоскости. В этом случае размер D (для изометрии, рис.9), D/2- для фронтальной диметрии (рис.10) откладываем по оси y, а размер S – по оси z. В этой проекции сокращаются также стороны шестиугольника, расположенные параллельно оси y (размер D/4 – рис.10).

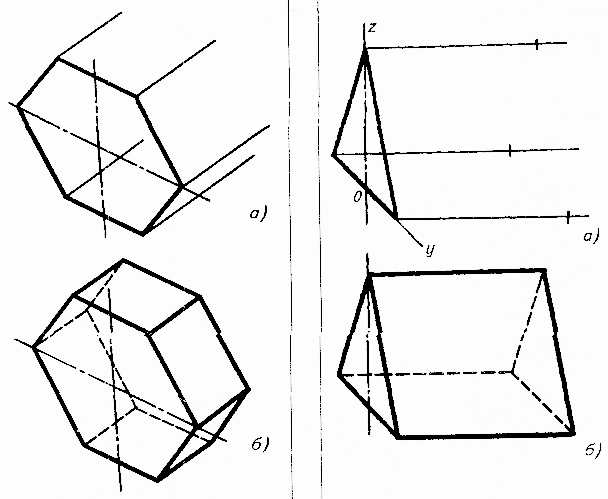
Построение аксонометрических проекций призм:

сначала строим проекции видимого основания (плоской фигуры), например в профильной плоскости. Через его вершины проводим прямые, параллельные оси х, и откладываем на них высоту (длину) призмы. Полученные точки соединяем отрезками прямых и обводим линии видимого контура (рис.11).

Построение аксонометрических проекций пирамид:

сначала строим проекцию основания пирамиды (плоской фигуры) и через точку О – центр тяжести полученной на плоскости фигуры – проводим вертикальную ось z. На этой оси откладываем высоту пирамиды – строим вершину. Полученные точки соединяем и обводим линии видимого контура (рис.12).