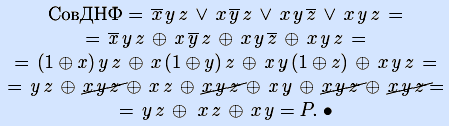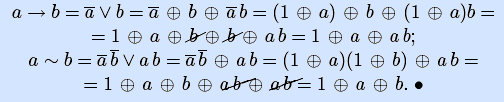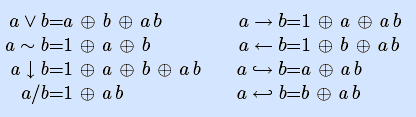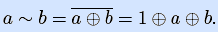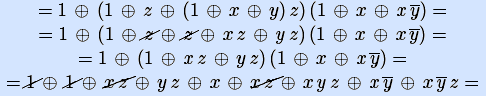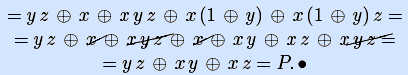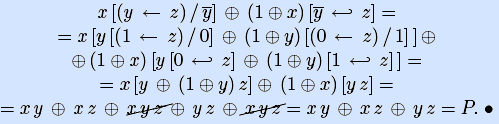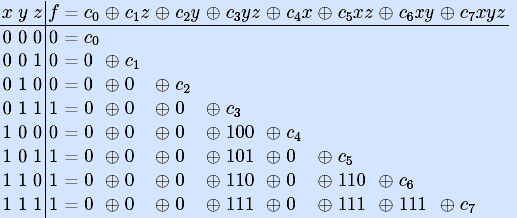Думаю, каждый, кто изучал или изучает в университете дискретную математику, знаком с понятием многочлена Жегалкина.
Главная особенность этих многочленов состоит в том, что любую булеву функцию можно представить полиномом Жегалкина, причем единственным образом.
Чаще всего для построения полиномов Жегалкина студентам предлагаются два метода построения таких полиномов: метод неопределенных коэффициентов и метод эквивалентных преобразований.
Расчеты с использованием данных методов часто оказываются громоздкими. По невнимательности допустить ошибку не составляет труда.
Под катом приведен один удобный алгоритм, для построения полиномов Жегалкина, который студенты воспринимают «на ура», т.к. требует только выполнение «механических действий» без применения каких-либо умственных усилий. Краткое описание метода можно найти в Википедии, но на мой взгляд по нему не совсем понятно, как быстро проводить вычисления. Мне метод известен под названием «метод треугольника Паскаля».
Порядок проведения вычислений проще показать на примере. Далее я буду по шагам показывать, как должен выглядеть расчет на бумаге (или как его удобно проводить).
- Метод треугольника Паскаля
- Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
- Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
- Полнота
- Существование и единственность представления Теорема Жегалкина: Каждая булева функция единственным образом представляется в виде полинома Жегалкина. Заметим, что различных булевых функций от $n$ переменных $2^ $ штук. При этом конъюнкций вида $x_ ldots x_ $ существует ровно $2^n$, так как из $n$ возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит $0$ или $1$, то есть существует $2^ $ различных полиномов Жегалкина от $n$ переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него . Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом. Построение полинома Жегалкина Существует несколько способов построения полинома Жегалкина. По таблице истинности Пусть для функции $f(x_1,x_2,dots,x_n)$ задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что $ a oplus 1 = bar $, а $ a oplus 0 = a$. За каждую подстановку находим только один коэффициент. Пример: Дана функция $f(x_1,x_2,x_3,x_4)$ и её таблица истинности: $x_1$ $x_2$ $x_3$ $x_4$ $f(x_1,x_2,x_3,x_4)$ 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 1 0 1 1 1 1 1 0 0 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 Построим для неё полином Жегалкина: $f(x_1,x_2,x_3,x_4) = a_ oplus a_ x_1 oplus a_ x_2 oplus a_ x_3 oplus a_ x_4 oplus a_ x_1 x_2 oplus a_ x_1 x_3 oplus a_ x_1 x_4 oplus \ oplus a_ x_2 x_3 oplus a_ x_2 x_4 oplus a_ x_3 x_4 oplus a_ x_1 x_2 x_3 oplus a_ x_1 x_2 x_4 oplus \ oplus a_ x_1 x_3 x_4 oplus a_ x_2 x_3 x_4 oplus a_ x_1 x_2 x_3 x_4$ Так как $f(0,0,0,0) = 0$, то $a_ = 0$. Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы: $f(1,0,0,0) = a_ oplus a_ = 1 Rightarrow a_ = 1$ $f(0,1,0,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(0,0,1,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(0,0,0,1) = a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(1,1,0,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$ $f(1,0,1,0) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ $f(1,0,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ $f(0,1,1,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 1$ $f(0,1,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(0,0,1,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(1,1,1,0) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$ $f(1,1,0,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(1,0,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$ $f(0,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ $f(1,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus \ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ Таким образом, полином Жегалкина выглядит так: $f(x_1,x_2,x_3,x_4) = x_1 oplus x_1 x_3 oplus x_1 x_4 oplus x_2 x_3 oplus x_2 x_3 x_4 oplus x_1 x_2 x_3 x_4$ Преобразование дизъюнктивной нормальной формы Этот способ основан на том, что $ X oplus 1 = bar $. Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю , а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу: $ A lor B = AB oplus A oplus B $ $ (1) $. Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ. Пример: Дана функция в ДНФ $ f(x_1,x_2,x_3,x_4) = (x_1 land x_2 land neg x_3 land x_4) lor (neg x_1 land neg x_4) lor (x_1 land x_2) lor x_2 $, построим полином Жегалкина. Запишем функцию так: $f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 + neg x_1 neg x_4 + x_1 x_2 + x_2$; Сгруппируем слагаемые и воспользуемся преобразованием (1): $f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_1 x_2 neg x_3 x_4 neg x_1 neg x_4) + (x_1 x_2 oplus x_2 oplus oplus x_1 x_2 x_2)$ Воспользуемся свойствами конъюнкции $A land A = A$ и $neg A land A = 0$, а также тем, что $A oplus A = 0$, и упростим выражение: $f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) + x_2$ Ещё раз воспользуемся преобразованием (1): $f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) x_2$ Раскроем скобку по алгебраическим правилам: $f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus x_1 x_2 x_2 neg x_3 x_4 oplus neg x_1 x_2 neg x_4$ Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ: $f(x_1,x_2,x_3,x_4) = neg x_1 neg x_4 oplus x_2 oplus neg x_1 x_2 neg x_4$ Заменим отрицание на прибавление $1$: $f(x_1,x_2,x_3,x_4) = (x_1 oplus 1) (x_4 oplus 1) oplus x_2 oplus (x_1 oplus 1) x_2 (x_4 oplus 1)$ $f(x_1,x_2,x_3,x_4) = x_1 x_4 oplus x_1 oplus x_4 oplus 1 oplus x_2 oplus x_1 x_2 x_4 oplus x_1 x_2 oplus x_2 x_4 oplus x_2$ Выкинем парные слагаемые и получим окончательную формулу: $f(x_1,x_2,x_3,x_4) = x_1 x_2 x_4 oplus x_1 x_2 oplus x_1 x_4 oplus x_2 x_4 oplus x_1 oplus x_4 oplus 1$ Метод треугольника Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами: Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от $000dots00$ до $111dots11$. Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности. Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже. Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности. Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке $111$ соответствует член $ABC$, ячейке $101$ — член $AC$, ячейке $010$ — член $B$, ячейке $000$ — член $1$ и т.д. Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина. Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций. Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных $P(A,B,C)$ показан на рисунке. Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца $»P»$ таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2. Таким образом, в первом столбце сверху записан коэффициент $ a_0 = P(0,0,0) $, во втором — $ a_1 = P(0,0,0) oplus P(0,0,1) $, в третьем — $ a_2 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) = P(0,0,0) oplus P(0,1,0) $, $ a_3 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1) = \ = P(0,0,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1), $ и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически. Преобразование Мёбиуса Пусть задана булева функция $f: B^n rightarrow B, ;; B= $. Любая булева функция представима в виде полинома Жегалкина, притом единственным образом. Пусть $ i = (i_1, i_2, .. i_n), ;; i_k in $, и введем обозначение $ x ^ sim left[begin x,;; i_k=1 1, ;; i_k=0end right. $ Тогда полином Жегалкина можно записать как: $ f(x) = bigopluslimits_i alpha_i cdot x_1^ cdot x_2^ cdot$$dots$$cdot x_n^ $, где $alpha_i in $. Множество коэффициентов $ $ можно рассматривать как функцию $alpha$, заданной на множестве индексов $ i = (i_1, i_2, dots i_n)$, то есть $alpha: i mapsto alpha_i$. Очевидно, функцию $ f $ можно записать и следующим образом: $ f(x) = bigoplus limits_i alpha_i cdot [x_1 , ; $ если $ ;; i_1] cdot [x_2 , ; $ если $ ;; i_2] cdot$$dots$$cdot [x_n , ; $ если $ ;; i_n]$. Тут запись $[x_k , ; $ если $ ; i_k]$ означает, что элелемент $ x_k $ присутствует в соответствующем члене полинома только если $ i_k = 1 $. Тогда если для какого-то $x$, $i succ x$* ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. Отсюда ясно, что $ f(x) = bigoplus limits_ alpha_i $ $ (2) $ Найдем отображение $ f mapsto alpha$ . $*$ $i succ x$ обозначает, что $x$ «меньше» $i$ как последовательность бит Теорема: Пусть задана функция $ f $. Тогда функцию $ alpha_x $ можно найти по формуле: $alpha_x = bigoplus limits_ f(j)$ (3) Докажем при помощи индукции по количеству единиц в векторе $ x $ и для удобства обозначим это количество единиц $ wt(x) $. 1) База: если $ x = 0 $, то, очевидно $ f(0) = alpha_0 $ 2) Пускай теорема справедлива для всех сумм $wt(x) Огравление $Rightarrow $ Нахождение полинома жегалкина методом треугольника Рассмотрим алгоритмы построения полинома Жегалкина булевой функции, заданной различными способами, а именно: совершенной ДНФ, произвольной ДНФ, формулой и таблицей истинности. Алгоритм построения полинома Жегалкина по СовДНФ (основан на доказательстве теоремы о существовании полинома Жегалкина). Начало. Задана совершенная ДНФ функции f(x1, …, xn). Шаг 1. Заменяем каждый символ дизъюнкции на символ дизюнкции с исключением. Шаг 2. Заменяем каждую переменную с инверсией x равносильной формулой x 1. Шаг 3. Раскрываем скобки. Шаг 4. Вычеркиваем из формулы пары одинаковых слагаемых. Конец. Получен полином Жегалкина функции f(x1, …, xn). Пример. Найдем полином Жегалкина мажоритарной булевой функции по ее совершенной ДНФ. Алгоритм построения полинома Жегалкина по ДНФ (основан на равносильности K1 K2= K1 K2 K1K2). Начало. Задана произвольная ДНФ функции f(x1, …, xn). Шаг 1. Разбиваем ДНФ на пары конъюнкций, предпочтительно ортогональных (если число конъюнкций нечетно, одна из них остается без пары). Шаг 2. Заменяем дизъюнкцию каждой пары конъюнкций K1 K2 формулой K1 K2 K1K2 или формулой K1 K2, если K1 и K2 ортогональны. Шаг 3. В полученной формуле находим очередную дизъюнкцию A1 A2и заменяем ее формулой A1 A2 A1A2. Повторяем шаг 3 до тех пор, пока это возможно. Шаг 4. Заменяем каждую переменную с инверсией x равносильной формулой x 1. Шаг 5. Раскрываем скобки. Шаг 6. Вычеркиваем из формулы пары одинаковых слагаемых. Конец. Получен полином Жегалкина функции f(x1, …, xn). Пример. Найдем полином Жегалкина мажоритарной функции по ДНФ. Отметим, что полиномы мажоритарной функции, полученные в двух последних примерах, совпадают с точностью до порядка конъюнкций, и это естественно (по теореме о единственности полинома Жегалкина). Способ 1 основан на предварительном преобразовании формулы в ДНФ (любым известным нам способом). Затем ДНФ преобразуется в полином Жегалкина по только что изученному алгоритму. Примеры. Получим полиномы Жегалкина двух элементарных булевых функций: импликации и эквивалентности, представив их предварительно кратчайшими ДНФ. Аналогично можно получить полиномы Жегалкина всех элементарных булевых функций (оставим читателю их вывод). Константы 0 и 1, тождественная функция, а также конъюнкция ab и дизъюнкция с исключением ab уже являются полиномами Жегалкина. Полином Жегалкина инверсии a =1a. Заметим, что некоторые из приведенных полиномов могут быть получены гораздо проще, в частности, Способ 2. Если булева функций задана произвольной формулой, то ее полином Жегалкина можно получить подстановкой в формулу вместо элементарных булевых функций их полиномов. Пример. Найдем полином Жегалкина мажоритарной функции, заданной формулой: [ подставим в формулу полином Жегалкина штриха Шеффера 1 ab при a=(xy) z, b=x y ] [ подставим полиномы Жегалкина обратной импликации 1 b ab при a=xy, b=z и импликации 1 a ab при a=x, b= y ] [ подставим полином Жегалкина эквивалентности 1 x y, раскроем скобки, и вычеркнем появившиеся при этом пары одинаковых слагаемых ] [заменим инверсию ее полиномом Жегалкина, раскроем скобки и вычеркнем пары одинаковых слагаемых ] Полином, естественно, совпадает с полученными ранее по совершенной и произвольной ДНФ. Способ 3. Если булева функций задана произвольной формулой, то ее полином Жегалкина можно получить, используя специальное разложение функции. Определение. Разложением Дэвио называется следующее разложение булевой функции f(x1, …, xn по переменной xi: Разложение Дэвио непосредственно следует из разложения Шеннона, если учесть, что слагаемые в последнем ортогональны, и что x i=xi 1. Пример. Найдем разложение Дэвио по переменной x мажоритарной булевой функции, заданной формулой. Для получения полинома Жегалкина необходимо продолжить разложение подформул, не являющихся дизъюнкцией с исключением элементарных конъюнкций, пока не получится формула над <,, – >. Если в такой формуле заменить инверсии x на x 1, раскрыть скобки и вычеркнуть пары одинаковых слагаемых, то получится полином Жегалкина. Пример. Продолжив предыдущий пример, получим полином Жегалкина мажоритарной функции. Для этого разложим подформулы (y z) / y и y z по переменной y: Полином Жегалкина, естественно, совпадает с полученными ранее. Алгоритм построения полинома Жегалкина по таблице истинности (основан на методе неопределенных коэффициентов). Продемонстрируем идею метода на примере произвольной булевой функции двух аргументов f(x,y). Представим ее полиномом Жегалкина в форме с коэффициентами Подставив в данное равенство наборы значений аргументов, получим систему из четырех линейных уравнений с четырьмя неизвестными коэффициентами: c0, c1 c2, c3. f(0,0) = c0 c10 c20 c30 0 = c0 f(0,1) = c0 c11 c20 c30 1 = c0 c1 f(1,0) = c0 c10 c21 c31 0 = c0 c2 f(1,1) = c0 c11 c21 c31 1 = c0 c1 c2 c3 Заметим, что наборы подставлены в равенство в естественном порядке, и система имеет треугольный вид: в первом уравнении обратились в ноль все слагаемые, следующие за c0, во втором – следующие за c1 и так далее. Значит, коэффициент c0 можно получить из первого уравнения и подставить его в остальные. Тогда c1 можно получить из второго уравнения, и так далее. В общем случае для функции n аргументов получается система треугольного вида из 2 n линейных уравнений с 2 n неизвестными – коэффициентами полинома Жегалкина. Пример. Найдем полином Жегалкина мажоритарной булевой функции, заданной таблицей истинности, последовательно вычисляя коэффициенты полинома и подставляя их в остальные уравнения. Из первого уравнения следует, что c0=0. Из второго и третьего уравнений следует, что c1=0 и c2=0, значит, c1z и c2y тождественно равны нулю. Из четвертого уравнения получаем c3=1, значит, надо вычислять значения конъюнкции c3yz в остальных уравнениях. Аналогично получаем c4=0, c5=1, c6=1 и c7=0. Найден вектор коэффициентов полинома Жегалкина мажоритарной функции π=00010110, и сам полином P=yz xz xy, который, естественно, совпадает с полученными ранее. •
- Построение полинома Жегалкина
- По таблице истинности
- Преобразование дизъюнктивной нормальной формы
- Метод треугольника
- Преобразование Мёбиуса
- Нахождение полинома жегалкина методом треугольника
- 🌟 Видео
Видео:A.2.19 Полином ЖегалкинаСкачать

Метод треугольника Паскаля
Требуется построить полином Жегалкина для функции f. Для примера, в качестве функции f возьмем функцию голосования .
Шаг 1. Строим таблицу значений функции (строки в таблице идут в порядке возрастания двоичных кодов). Таблицу лучше разместить в левой части листа.
Шаг 2. Построение треугольника.
Для этого берем вектор значения функции и выписываем его напротив первой строки таблицы:
Далее заполняем треугольник, складывая попарно соседние значения по модулю 2, результат сложения выписываем ниже.
Продолжаем вычисления, пока в строке не останется лишь одна цифра.
Шаг 3. Построение полинома Жегалкина.
Нас интересует левая сторона треугольника (значения выделены жирным):
Числа на левой стороне (выделены жирным шрифтом) треугольника есть коэффициенты полинома при монотонных конъюнкциях, соответствующих наборам значений переменных.
Теперь выпишем для наглядности эти конъюнкции. Конъюнкции выписываем по двоичным наборам в левой части таблицы по следующему принципу: если напротив переменной xi стоит 1, то переменная входит в конъюнкцию; в противном случае переменная отсутствует в конъюнкции. Набору (0,0,0) соответствует константа 1.
Если принцип получения конъюнкций понятен, то столбец с ними можно (даже лучше) не выписывать, а сразу переходить к построению полинома.
Для построения полинома нужны только конъюнкции из строк с единицами на левой стороне треугольника.
Это и есть конъюнкции, входящие в состав полинома Жегалкина. Осталось лишь выписать сам полином:
Если переменных в функции не 3, а 4 или больше, то метод работает без изменений, только увеличатся размеры таблиц. Тем не менее, в отличие от метода неопределенных коэффициентов, расчеты можно без особых усилий выполнить на листе бумаги.
Видео:Многочлен полином Жегалкина Метод треугольника Паскаля Преобразование формулСкачать

Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
- Услуги проектирования
- Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв]
- Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Видео:Многочлен полином Жегалкина Метод неопределенных коэффициентов Метод треугольника ПаскаляСкачать

Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Полином Жегалкина — многочлен над кольцом $mathbb _2$, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой .
Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.
Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также константы
Формально полином Жегалкина можно представить в виде
или в более формализованном виде как:
$P = a oplus bigoplus_ < begin 1leq i_1 Примеры полиномов Жегалкина:
- $ P = B oplus AB;$
- $ P = X oplus YZ oplus ABX oplus ABDYZ;$
- $ P = 1 oplus A oplus ABD.$
Видео:Полином ЖегалкинаСкачать

Полнота
По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали
- Хотя бы одна функция, не сохраняющая $0$;
- Хотя бы одна функция, не сохраняющая $1$;
- Хотя бы одна нелинейная функция;
- Хотя бы одна немонотонная функция;
- Хотя бы одна несамодвойственная функция.
Исходя из этого, система функций $bigllangle wedge, oplus, 1 bigrrangle$ является полной:
| $x_0$ | $x_1$ | $dots$ | $x_n$ | $1$ | $land$ | $oplus$ |
| $0$ | $0$ | $dots$ | $0$ | $1$ | $0$ | $0$ |
| $1$ | $0$ | $dots$ | $0$ | $1$ | $0$ | $1$ |
| $vdots$ | $vdots$ | $vdots$ | $vdots$ | $vdots$ | $vdots$ | $vdots$ |
| $1$ | $1$ | $dots$ | $1$ | $1$ | $1$ | $0$ |
| . | . | . | сохраняет 0 | $0$ | $1$ | $1$ |
| . | . | . | сохраняет 1 | $1$ | $1$ | $0$ |
| . | . | . | самодвойственная | $0$ | $0$ | $0$ |
| . | . | . | монотонная | $1$ | $1$ | $0$ |
| . | . | . | линейная | $1$ | $0$ | $1$ |
На основе этой системы и строятся полиномы Жегалкина.
Видео:Полином ЖегалкинаСкачать

Существование и единственность представления
Теорема Жегалкина: Каждая булева функция единственным образом представляется в виде полинома Жегалкина.
Заметим, что различных булевых функций от $n$ переменных $2^ $ штук. При этом конъюнкций вида $x_ ldots x_ $ существует ровно $2^n$, так как из $n$ возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит $0$ или $1$, то есть существует $2^ $ различных полиномов Жегалкина от $n$ переменных.
Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него . Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.
Видео:Представление в виде Полинома Жегалкина функции заданной в виде СДНФСкачать
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
По таблице истинности
Пусть для функции $f(x_1,x_2,dots,x_n)$ задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что $ a oplus 1 = bar $, а $ a oplus 0 = a$. За каждую подстановку находим только один коэффициент.
Пример: Дана функция $f(x_1,x_2,x_3,x_4)$ и её таблица истинности:
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | $f(x_1,x_2,x_3,x_4)$ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Построим для неё полином Жегалкина:
$f(x_1,x_2,x_3,x_4) = a_ oplus a_ x_1 oplus a_ x_2 oplus a_ x_3 oplus a_ x_4 oplus a_ x_1 x_2 oplus a_ x_1 x_3 oplus a_ x_1 x_4 oplus \ oplus a_ x_2 x_3 oplus a_ x_2 x_4 oplus a_ x_3 x_4 oplus a_ x_1 x_2 x_3 oplus a_ x_1 x_2 x_4 oplus \ oplus a_ x_1 x_3 x_4 oplus a_ x_2 x_3 x_4 oplus a_ x_1 x_2 x_3 x_4$
Так как $f(0,0,0,0) = 0$, то $a_ = 0$.
Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:
$f(1,0,0,0) = a_ oplus a_ = 1 Rightarrow a_ = 1$
$f(0,1,0,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(0,0,1,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(0,0,0,1) = a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(1,1,0,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$
$f(1,0,1,0) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
$f(1,0,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
$f(0,1,1,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 1$
$f(0,1,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(0,0,1,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(1,1,1,0) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$
$f(1,1,0,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(1,0,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$
$f(0,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
$f(1,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus \ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
Таким образом, полином Жегалкина выглядит так:
$f(x_1,x_2,x_3,x_4) = x_1 oplus x_1 x_3 oplus x_1 x_4 oplus x_2 x_3 oplus x_2 x_3 x_4 oplus x_1 x_2 x_3 x_4$
Преобразование дизъюнктивной нормальной формы
Этот способ основан на том, что $ X oplus 1 = bar $. Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю , а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу: $ A lor B = AB oplus A oplus B $ $ (1) $.
Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.
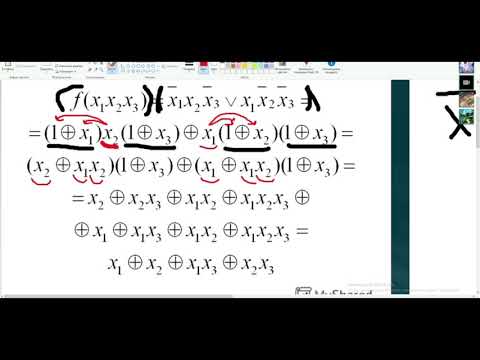
Пример: Дана функция в ДНФ $ f(x_1,x_2,x_3,x_4) = (x_1 land x_2 land neg x_3 land x_4) lor (neg x_1 land neg x_4) lor (x_1 land x_2) lor x_2 $, построим полином Жегалкина.
Запишем функцию так:
$f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 + neg x_1 neg x_4 + x_1 x_2 + x_2$;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
$f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_1 x_2 neg x_3 x_4 neg x_1 neg x_4) + (x_1 x_2 oplus x_2 oplus oplus x_1 x_2 x_2)$
Воспользуемся свойствами конъюнкции $A land A = A$ и $neg A land A = 0$, а также тем, что $A oplus A = 0$, и упростим выражение:
$f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) + x_2$
Ещё раз воспользуемся преобразованием (1):
$f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) x_2$
Раскроем скобку по алгебраическим правилам:
$f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus x_1 x_2 x_2 neg x_3 x_4 oplus neg x_1 x_2 neg x_4$
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
$f(x_1,x_2,x_3,x_4) = neg x_1 neg x_4 oplus x_2 oplus neg x_1 x_2 neg x_4$
Заменим отрицание на прибавление $1$:
$f(x_1,x_2,x_3,x_4) = (x_1 oplus 1) (x_4 oplus 1) oplus x_2 oplus (x_1 oplus 1) x_2 (x_4 oplus 1)$
$f(x_1,x_2,x_3,x_4) = x_1 x_4 oplus x_1 oplus x_4 oplus 1 oplus x_2 oplus x_1 x_2 x_4 oplus x_1 x_2 oplus x_2 x_4 oplus x_2$
Выкинем парные слагаемые и получим окончательную формулу:
$f(x_1,x_2,x_3,x_4) = x_1 x_2 x_4 oplus x_1 x_2 oplus x_1 x_4 oplus x_2 x_4 oplus x_1 oplus x_4 oplus 1$
Метод треугольника
Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
- Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от $000dots00$ до $111dots11$.
- Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
- Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
- Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
- Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке $111$ соответствует член $ABC$, ячейке $101$ — член $AC$, ячейке $010$ — член $B$, ячейке $000$ — член $1$ и т.д.
- Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.
Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций.
Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных $P(A,B,C)$ показан на рисунке.
Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца $»P»$ таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2.
Таким образом, в первом столбце сверху записан коэффициент $ a_0 = P(0,0,0) $,
во втором — $ a_1 = P(0,0,0) oplus P(0,0,1) $,
в третьем — $ a_2 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) = P(0,0,0) oplus P(0,1,0) $,
$ a_3 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1) = \ = P(0,0,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1), $
и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически.
Преобразование Мёбиуса
Пусть задана булева функция $f: B^n rightarrow B, ;; B= $. Любая булева функция представима в виде полинома Жегалкина, притом единственным образом.
Пусть $ i = (i_1, i_2, .. i_n), ;; i_k in $, и введем обозначение $ x ^ sim left[begin x,;; i_k=1 1, ;; i_k=0end right. $
Тогда полином Жегалкина можно записать как: $ f(x) = bigopluslimits_i alpha_i cdot x_1^ cdot x_2^ cdot$$dots$$cdot x_n^ $, где $alpha_i in $.
Множество коэффициентов $ $ можно рассматривать как функцию $alpha$, заданной на множестве индексов $ i = (i_1, i_2, dots i_n)$, то есть $alpha: i mapsto alpha_i$.
Очевидно, функцию $ f $ можно записать и следующим образом: $ f(x) = bigoplus limits_i alpha_i cdot [x_1 , ; $ если $ ;; i_1] cdot [x_2 , ; $ если $ ;; i_2] cdot$$dots$$cdot [x_n , ; $ если $ ;; i_n]$.
Тут запись $[x_k , ; $ если $ ; i_k]$ означает, что элелемент $ x_k $ присутствует в соответствующем члене полинома только если $ i_k = 1 $. Тогда если для какого-то $x$, $i succ x$* ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. Отсюда ясно, что $ f(x) = bigoplus limits_ alpha_i $ $ (2) $ Найдем отображение $ f mapsto alpha$ .
$*$ $i succ x$ обозначает, что $x$ «меньше» $i$ как последовательность бит
Теорема: Пусть задана функция $ f $. Тогда функцию $ alpha_x $ можно найти по формуле: $alpha_x = bigoplus limits_ f(j)$ (3)
Докажем при помощи индукции по количеству единиц в векторе $ x $ и для удобства обозначим это количество единиц $ wt(x) $.
1) База: если $ x = 0 $, то, очевидно $ f(0) = alpha_0 $
2) Пускай теорема справедлива для всех сумм $wt(x) Огравление $Rightarrow $
Видео:Лекция 2. Полином Жегалкина (теоретическая часть)Скачать

Нахождение полинома жегалкина методом треугольника
Рассмотрим алгоритмы построения полинома Жегалкина булевой функции, заданной различными способами, а именно: совершенной ДНФ, произвольной ДНФ, формулой и таблицей истинности.
Алгоритм построения полинома Жегалкина по СовДНФ (основан на доказательстве теоремы о существовании полинома Жегалкина).
Начало. Задана совершенная ДНФ функции f(x1, …, xn).
Шаг 1. Заменяем каждый символ дизъюнкции на символ дизюнкции с исключением.
Шаг 2. Заменяем каждую переменную с инверсией x равносильной формулой x 
Шаг 3. Раскрываем скобки.
Шаг 4. Вычеркиваем из формулы пары одинаковых слагаемых.
Конец. Получен полином Жегалкина функции f(x1, …, xn).
Пример. Найдем полином Жегалкина мажоритарной булевой функции по ее совершенной ДНФ.
Алгоритм построения полинома Жегалкина по ДНФ (основан на равносильности K1 


Начало. Задана произвольная ДНФ функции f(x1, …, xn).
Шаг 1. Разбиваем ДНФ на пары конъюнкций, предпочтительно ортогональных (если число конъюнкций нечетно, одна из них остается без пары).
Шаг 2. Заменяем дизъюнкцию каждой пары конъюнкций K1 



Шаг 3. В полученной формуле находим очередную дизъюнкцию A1 


Шаг 4. Заменяем каждую переменную с инверсией x равносильной формулой x 
Шаг 5. Раскрываем скобки.
Шаг 6. Вычеркиваем из формулы пары одинаковых слагаемых.
Конец. Получен полином Жегалкина функции f(x1, …, xn).
Пример. Найдем полином Жегалкина мажоритарной функции по ДНФ.
Отметим, что полиномы мажоритарной функции, полученные в двух последних примерах, совпадают с точностью до порядка конъюнкций, и это естественно (по теореме о единственности полинома Жегалкина).
Способ 1 основан на предварительном преобразовании формулы в ДНФ (любым известным нам способом). Затем ДНФ преобразуется в полином Жегалкина по только что изученному алгоритму.
Примеры. Получим полиномы Жегалкина двух элементарных булевых функций: импликации и эквивалентности, представив их предварительно кратчайшими ДНФ.
Аналогично можно получить полиномы Жегалкина всех элементарных булевых функций (оставим читателю их вывод).
Константы 0 и 1, тождественная функция, а также конъюнкция ab и дизъюнкция с исключением a

Заметим, что некоторые из приведенных полиномов могут быть получены гораздо проще, в частности,
Способ 2. Если булева функций задана произвольной формулой, то ее полином Жегалкина можно получить подстановкой в формулу вместо элементарных булевых функций их полиномов.
Пример. Найдем полином Жегалкина мажоритарной функции, заданной формулой:
[ подставим в формулу полином Жегалкина штриха Шеффера 1 

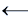

[ подставим полиномы Жегалкина обратной импликации 1 




[ подставим полином Жегалкина эквивалентности 1 

[заменим инверсию ее полиномом Жегалкина, раскроем скобки и вычеркнем пары одинаковых слагаемых ]
Полином, естественно, совпадает с полученными ранее по совершенной и произвольной ДНФ.
Способ 3. Если булева функций задана произвольной формулой, то ее полином Жегалкина можно получить, используя специальное разложение функции.
Определение. Разложением Дэвио называется следующее разложение булевой функции f(x1, …, xn по переменной xi:
Разложение Дэвио непосредственно следует из разложения Шеннона, если учесть, что слагаемые в последнем ортогональны, и что x i=xi 
Пример. Найдем разложение Дэвио по переменной x мажоритарной булевой функции, заданной формулой.
Для получения полинома Жегалкина необходимо продолжить разложение подформул, не являющихся дизъюнкцией с исключением элементарных конъюнкций, пока не получится формула над <
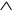

Пример. Продолжив предыдущий пример, получим полином Жегалкина мажоритарной функции. Для этого разложим подформулы (y 
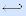
Полином Жегалкина, естественно, совпадает с полученными ранее.
Алгоритм построения полинома Жегалкина по таблице истинности (основан на методе неопределенных коэффициентов).
Продемонстрируем идею метода на примере произвольной булевой функции двух аргументов f(x,y). Представим ее полиномом Жегалкина в форме с коэффициентами
Подставив в данное равенство наборы значений аргументов, получим систему из четырех линейных уравнений с четырьмя неизвестными коэффициентами: c0, c1 c2, c3.
f(0,0) = c0 


f(0,1) = c0 



f(1,0) = c0 



f(1,1) = c0 





Заметим, что наборы подставлены в равенство в естественном порядке, и система имеет треугольный вид: в первом уравнении обратились в ноль все слагаемые, следующие за c0, во втором – следующие за c1 и так далее. Значит, коэффициент c0 можно получить из первого уравнения и подставить его в остальные. Тогда c1 можно получить из второго уравнения, и так далее.
В общем случае для функции n аргументов получается система треугольного вида из 2 n линейных уравнений с 2 n неизвестными – коэффициентами полинома Жегалкина.
Пример. Найдем полином Жегалкина мажоритарной булевой функции, заданной таблицей истинности, последовательно вычисляя коэффициенты полинома и подставляя их в остальные уравнения.
Из первого уравнения следует, что c0=0. Из второго и третьего уравнений следует, что c1=0 и c2=0, значит, c1z и c2y тождественно равны нулю. Из четвертого уравнения получаем c3=1, значит, надо вычислять значения конъюнкции c3yz в остальных уравнениях. Аналогично получаем c4=0, c5=1, c6=1 и c7=0. Найден вектор коэффициентов полинома Жегалкина мажоритарной функции π=00010110, и сам полином P=yz 

🌟 Видео
Многочлен полином Жегалкина Метод неопределенных коэффициентовСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Полином Жегалкина с нуля. Часть 1Скачать

СДНФ СКНФ Полином Жегалкина для логических выраженийСкачать

20-2 Полиномы ЖегалкинаСкачать

Многочлен Жегалкина.Скачать

Треугольник ПаскаляСкачать

ДМ 1 курс - 3 лекция - булевы функции, полиномы Жегалкина, критерий ПостаСкачать

Суммаризация нормальных форм двоичных функций. Полином ЖегалкинаСкачать

Метод неопределенных коэффициентов. 10 класс.Скачать

Как использовать метод неопределённых коэффициентов для минимизации ДНФ и КНФ? Душкин объяснитСкачать

Математическая логика и теория алгоритмов 4. Полиномы Жегалкина. ЗамыканиеСкачать

Логические уравнения. Полином Жегалкина. Разбор примеровСкачать