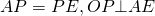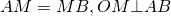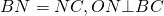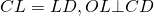Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.
Теорема
| Около любого треугольника можно описать окружность. |
- Доказательство
- Доказательство
- Доказательство
- Доказательство
- Доказательство
- Описанная окружность
- 2 Comments
- Love Soft
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Навигация
- Связь
- Содержание
- Четырехугольник
- Мнемоника
- Окружность вписанная в четырехугольник
- Почему нельзя вписать окружность?
- Задача
- Окружность, описанная около четырехугольника
- Задача 1
- Задача 2
- Задача 3
- Центр тяжести
- Распределительное свойство центров тяжести
- Центр тяжести четырехугольника
- Метод отвеса
- Метод балансировки
- С помощью геометрического разложения
- Центр тяжести объекта в форме буквы L
- Барицентр
- Барицентрическая система отсчета
- Барицентрические координаты
- Случай двух тел
- 🎥 Видео
Доказательство
Дано: произвольный 
Доказать: около 
Доказательство:
1. Проведем серединные перпендикуляры к сторонам 
Точка О равноудалена от вершин 

Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
| В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 . |
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).
Углы В и D — вписанные, тогда по теореме о вписанном угле: 















Верно и обратное утверждение:
| Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность. |
Доказательство
Дано: четырехугольник АВСD, 

Доказать: около АВСD можно описать окружность.
Доказательство:
Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).





Углы ВFD и FDE — вписанные. По теореме о вписанном угле 



















Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. 




Итак, мы получили, что 




Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
По теореме о сумме углов треугольника в 
















Подставим (3) и (4) в (2), получим:




















Примечание:
Окружность всегда можно описать:
Поделись с друзьями в социальных сетях:
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Описанная окружность
Что такое описанная окружность? Какими свойствами она обладает?
Описанная около выпуклого многоугольника окружность — это окружность, которая проходит через все вершины многоугольника.
Многоугольник, около которого описана окружность, называется вписанным.
В выпуклый многоугольник можно вписать окружность, если все серединные перпендикуляры к его сторонам пересекаются в одной точке.
Центр вписанной в многоугольник окружности — точка пересечения серединных перпендикуляров к его сторонам.
Центр описанной окружности равноудалён от вершин многоугольника.
Расстояние от центра до любой вершины многоугольника равно радиусу описанной окружности.

ABCDE — вписанный пятиугольник.
O — точка пересечения серединных перпендикуляров к сторонам ABCD, то есть

Расстояние от точки O до любой вершины равно радиусу:
Около любого правильного многоугольника можно описать окружность. В любой правильный многоугольник также можно вписать окружность. Центр вписанной и описанной окружности лежат в центре правильного многоугольника.
В отличие от вписанной окружности, общей формулы для нахождения радиуса описанной около многоугольника окружности нет. Радиус описанной окружности можно найти как радиус окружности, описанной около любого из треугольников, вершины которого являются вершинами описанного многоугольника.
Например, для описанного пятиугольника ABCDE радиус можно найти как радиус окружности, описанной около одного из треугольников ABC, ABD, ABE, BCD, BCE, ACD, ADE и т.д.
Формулы для нахождения радиуса описанной окружности существуют в частных случаях: для правильных многоугольников, треугольников, прямоугольника.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

2 Comments
Огромное спасибо за все статьи, что есть на этом сайте! Благодаря вам восполнила пробелы в теории, из-за которых не могла решить задачки, и теперь щёлкаю задания как орехи. Лучший сайт по геометрии!
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Love Soft
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация

Связь
Содержание
Видео:9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Четырехугольник
Видео:Радиус описанной окружностиСкачать

Мнемоника
для запоминания условий, для того чтобы можно было вписать или описать окружность в четырехугольнике, у меня в опорном конспекте (и отложилось, фактически само по себе, в голове): две картинки: дорожный знак «кирпич», на котором написано 180. И вторая картинка, это инопланетянин в квадратном шлеме с плюсами вместо ушей. Ну и чем более абсурдный образ, тем лучше. Я никогда не перепутаю эти условия потому что, например, знак «кирпич» — окружность снаружи, а надпись 180 – означает суму противоположных углов.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Окружность вписанная в четырехугольник
Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
Наоборот: если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Центр вписанной окружности лежит на пересечении биссектрис углов четырехугольника.
Почему нельзя вписать окружность?
в отличие от треугольника, далеко не во всякий четырехугольник можно поместить окружность так, чтобы она касалась всех его сторон.
Треугольник всегда является описанным – потому что во всякий треугольник можно вписать окружность. Чем же четырехугольник-то хуже? И вот оказывается, что чем-то, да хуже.
Представь себе, например, длинный прямоугольник. Как вот в него, спрашивается, можно вписать окружность? Конечно, никак. И это лишь один из примеров четырехугольника, в которой НЕЛЬЗЯ вписать окружность.
Задача
Видео:№200. Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около мноСкачать
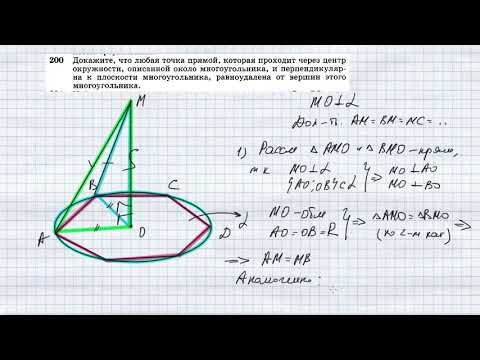
Окружность, описанная около четырехугольника
Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна ∠ϕ+∠γ=180∘.
И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна ∠ϕ+∠γ=180∘, то около него можно описать окружность.
Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам.
Около выпуклого четырехугольника описана окружность ⇔ ∠α=∠β.
Площадь вписанного четырехугольника вычисляется по формуле
где a, b, c, d – его стороны, p — полупериметр
Задача 1
Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Задача 2
Стороны AB, BC, CD, AD четырехугольника ABCD стягивают дуги описанной окружности, градусные меры которых равны соответственно 95 ∘ ,49 ∘ ,71 ∘ ,145 ∘ . Найдите угол B этого четырехугольника. Ответ дайте в градусах.
Угол B четырехугольника равен вписанному углу ABC. Этот угол опирается на дугу ADC, равную 145 ∘ +71 ∘ =216 ∘ . Так как вписанный угол равен половине дуги, на которую он опирается, то ∠B=∠ABC=108 ∘ .
Задача 3
Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB,BC,CD,DA, градусные величины которых относятся соответственно как 4:2:3:6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
Так как дуги AB,BC,CD,DA относятся как 4:2:3:6, то можно принять дугу AB за 4x, дугу BC за 2x, дугу CD за 3x и дугу DA за 6x. Так как все эти дуги в совокупности дают целую окружность, градусная мера которой равна 360∘, то 4x+2x+3x+6x=360∘, откуда x=24∘. Угол A равен вписанному углу BAD, опирающемуся на дугу BCD, равную 2x+3x=5x=120∘. Так как вписанный угол равен половине этой дуги, то ∠A=60∘.
Видео:Построить описанную окружность (Задача 1)Скачать

Центр тяжести
Центр тяжести системы материальных точек — обозначим через $m_k$ — массы точек, $x_k, y_k, z_k$ — координаты точек.
К каждой из точек приложен вектор величины $m_k$, все векторы параллельны и направлены в одну сторону.
Центр этих векторов есть точка с координатами $$M_x = sum m_k x_k, M_y = sum m_k y_k, M_z = sum m_k z_k$$
Если все точки имеют одинаковую массу, то $M = sum m_k$ — масса всей системы, тогда
$$M_x = M sum x_k, M_y = M sum y_k, M_z = M sum z_k$$
В математике и физике барицентр или геометрический центр области — это среднее арифметическое положений всех точек фигуры.
Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.
Центр масс (и центр тяжести в постоянном гравитационном поле) является средним арифметическим всех точек с учётом локальной плотности или удельного веса. Если физический объект имеет постоянную плотность, то его центр масс совпадает с барицентром фигуры той же формы.
Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.
Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильный многоугольник, правильный многогранник, цилиндр, прямоугольник, ромб, окружность, сфера, эллипс, эллипсоид, суперэллипс, суперэллипсоид, и т.д.) можно найти исходя исключительно из этого принципа.
В частности, барицентром параллелограмма является пересечение диагоналей. Вообще говоря, это неверно для других четырёхугольников.
Распределительное свойство центров тяжести
Если разделить систему материальных точек S на дне части S’ и S«, то ее центр тяжести есть в то же время центр тяжести двух масс М’ и М» систем S’ и S«, помещенных соответственно в центрах тяжести этих двух систем.
Центр тяжести четырехугольника
Центр тяжести площади четырехугольника определяется пересечением двух прямых, которые мы получаем, используя распределительное свойство центров тяжести.
Сначала делим четырехугольник диагональю на два треугольника. Центр тяжести четырехугольника лежит на прямой, соединяющей центры тяжести этих треугольников. Это первая искомая прямая.
Вторая искомая прямая получается аналогичным образом — разбивая четырехугольник на треугольники второй диагональю.
Центроид (барицентр или центр масс) произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника и отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам.
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершины.
Метод отвеса
Барицентр однородной плоской фигуры, такой как на рисунке ниже, можно найти экспериментально с использованием отвеса и булавки. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке. Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр.
Метод балансировки
Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.
С помощью геометрического разложения
Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур.
Рассмотрим пример. Фигуру на рисунке легко разделить на квадрат и треугольник с положительным знаком площади и круглое отверстие с отрицательным знаком площади.
Квадрат — пересечение диагоналей $(5, 5)$. Площадь 100.
Прямоугольный треугольник — отложить по трети катета от вершины прямого угла $(10+10/3,10/3) = (13.33; 3.33)$. Площадь 50.
Окружность — центр $(2.5; 12.5)$. Площадь $6.25pi = 19.63$
Та же формула применима для любого трёхмерного объекта, только вместо площадей берут объёмы частей тела.
Центр тяжести объекта в форме буквы L
Делим на два прямоугольника, находим центры каждого из них как пересечение диагоналей, соединяем. Барицентр фигуры должен лежать на этом отрезке AB.
Делим фигуру на два прямоугольника другим способом. Находим барицентры этих двух прямоугольников. Проводим отрезок, соединяющий центры. Барицентр фигуры должен лежать на этом отрезке CD.
Барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.
Барицентр
это цетр масс двух и более тел, которые вращаются друг около друга.
Чем массивнее одно из двух тел, тем ближе к нему барицентр. Для системы Луна-Земля барицентр расположен примерно на расстоянии 4 671 км от центра Земли, радиус планеты 6 378 км.
Барицентрическая система отсчета
International Celestial Reference System (ICRS, Международная небесная система координат или Международная система астрономических координат) — с 1998 года стандартная небесная система координат.
Началом отсчёта является барицентр Солнечной системы. Координаты в этой системе максимально приближены к экваториальным эпохи J2000.0 (расхождение составляет доли секунды дуги)
Оси системы зафиксированы в пространстве относительно квазаров, которые считаются наиболее удалёнными объектами наблюдаемой Вселенной. Их предполагаемое собственное движение настолько мало, что им можно пренебречь. Внедрение системы обусловлено необходимостью повышения точности астрономических измерений до 0,05″.
Полученная система координат независима от вращения Земли.
Барицентрические координаты
Пусть дан треугольник ABC. Тогда любую точку P в плоскости треугольника можно представить как центр некоторых масс α, β, γ, помещенных в его вершины A, B, C.
Тройка чисел (α, β, γ) называется барицентрическими координатами точки P относительно треугольника.
Барицентрические координаты точки определены с точностью до ненулевого множителя: все тройки (kα, kβ, kγ) при любом k ≠ 0 задают одну и ту же точку P. Любые три числа с ненулевой суммой являются барицентрическими координатами некоторой точки. Иногда барицентрическими координатами называют ту из пропорциональных троек, у которой сумма чисел равна единице. Соответствие между такими тройками и точками плоскости взаимно-однозначно.
Если точка P лежит внутри треугольника ABC, то ее барицентрические координаты пропорциональны площадям треугольников PAB, PBC и PCA. Для точек вне треугольника это тоже верно, только нужно брать ориентированные площади.
Случай двух тел
Два тела взаимодействуют только друг с другом. Тела вращаются поэллиптической орбите пример двойные звезды.
🎥 Видео
✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

вписанный и описанный четырехугольникСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать
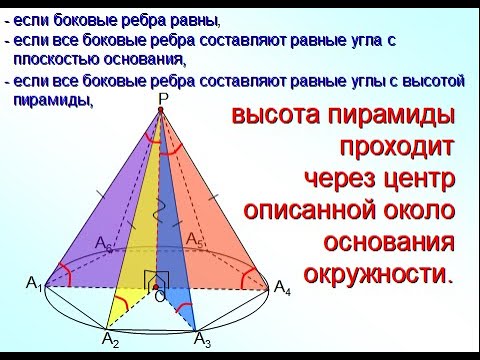
Центр окружности описанной вокруг треугольникаСкачать

11 класс, 44 урок, Описанный четырехугольникСкачать

Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Вписанные и описанные окружности (в треугольник)Скачать

Центр описанной окружностиСкачать

Геометрия Четырехугольник оказался вписанным Задача №26 ОГЭСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать