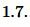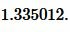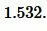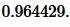Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Радиус вписанной в треугольник окружности онлайн
- 1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
- 2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
- 3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
- 4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
- math4school.ru
- Треугольники
- Основные свойства
- Равенство треугольников
- Подобие треугольников
- Медианы треугольника
- Биссектрисы треугольника
- Высоты треугольника
- Серединные перпендикуляры
- Окружность, вписанная в треугольник
- Окружность, описанная около треугольника
- Расположение центра описанной окружности
- Равнобедренный треугольник
- Равносторонний треугольник
- Прямоугольный треугольник
- Вневписанные окружности
- Теоремы синусов, косинусов, тангенсов; формулы Мольвейде
Видео:Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный треугольник | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
| Равнобедренный треугольник | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
| Равносторонний треугольник | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольный треугольник | |||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Построение равностронего треугольника.Скачать

Радиус вписанной в треугольник окружности онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
Пусть известна площадь S треугольника и полупериметр
| ( small p=frac ) | (1) |
где a, b, c стороны треугольника (Рис.1).
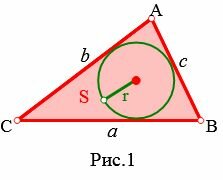 |
Найдем радиус вписанной в треугольник окружности r.
Из центра O вписанной в треугольник окружности проведем перпендикуляры к сторонам треугольника. Все эти перпендикуляры равны радиусу r вписанной в треугольник окружности (Рис.2).
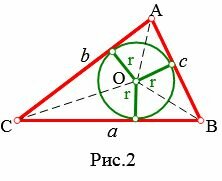 |
Прямыми OA, OB, OC разделим треугольник ABC на три треугольника: AOC, COB, AOB. Найдем площадь треугольников AOC, COB, AOB:
| ( small S_=frac cdot r cdot b ,) ( small S_=frac cdot r cdot c, ) ( small S_=frac cdot r cdot a ) | (2) |
| ( small S=S_+S_+S_)( small =frac cdot r cdot b ) ( small +frac cdot r cdot c ) ( small +frac cdot r cdot a ) ( small =frac cdot r cdot ( a+b+c) ) | (3) |
| ( small S=r cdot p. ) | (4) |
Найдем радиус r вписанной в треугольник окружности из равенства (4):
| ( small r=frac. ) | (5) |
Пример 1. Известны площадь ( small S=17 ) и полупериметр ( small p=10 ) треугольника. Найти радиус вписанной в треугольник окружности.
Решение. Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулой (5).
Подставим значения ( small S=17 ) и ( small p=10 ) в (5):
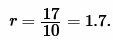 |
Ответ:
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
Пусть известны три стороны треугольника: a, b, c. Найдем радиус вписанной в треугольник окружности (Рис.3).
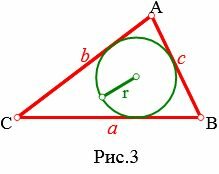 |
Площадь треугольника по трем сторонам вычисляется из формулы:
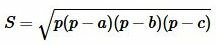 | (6) |
где полупериметр p вычисляется из формулы (1).
Подставляя (6) в (5), получим формулу радиуса вписанной в треугольник окружности:
| ( small r=sqrt<frac>, ) | (7) |
Пример 2. Известны стороны треугольника: ( small a=15 ,; b=7, ; c=9.) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала полупериметр треугольника из формулы (1):
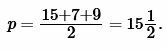 |
Подставим значения ( small a,; b, ; c, ; p ) в (7):
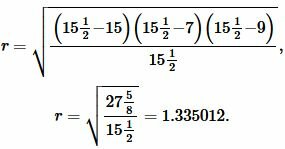 |
Ответ:
Видео:Построить описанную окружность (Задача 1)Скачать

3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
Пусть известны стороны b и c треугольника и угол A между ними (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
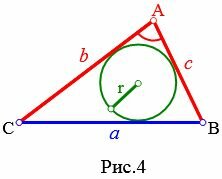 |
Из теоремы косинусов найдем сторону a треугольника:
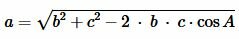 | (8) |
Далее, для вычисления радиуса вписанной в треугольник окружности, воспользуемся формулой (7), где полупериметр p вычисляется из (1).
Пример 3. Известны стороны треугольника: ( small b=9 ,; c=7, ; ) и угол меджу ними A=30°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала сторону a треугольника из формулы (8):
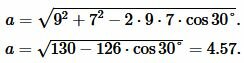 |
Далее найдем p из формулы (1):
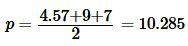 |
Подставим значения ( small a,; b, ; c, ; p ) в (7):
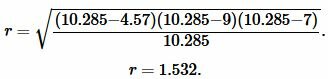 |
Ответ:
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
Пусть известны сторона a треугольника и прилежащие два угла B и C (Рис.5). Найдем радиус вписанной в треугольник окружности.
 |
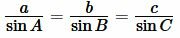 |
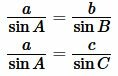 |
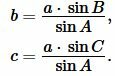 | (9) |
Поскольку сумма углов треугольника равна 180°, то имеем ( small angle A=180°-(angle B+angle C). ) Из формул приведения тригонометрических функций имеем: ( small sin A=sin (180°-( B+ C)) ) ( small =sin (B+C). ) Тогда формулы (9) можно переписать так:
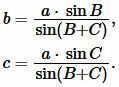 | (10) |
Получая значения сторон b, c из (10) и значение p из (1), можно найди радиус вписанной в треугольник окружности из формулы (7). Таким образом, для нахождения радиуса вписанной в треугольник окружности через сторону и прилежащим двум углам применяется формула
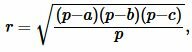 | (11) |
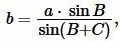 | (12) |
 , , | (13) |
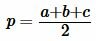 . . | (14) |
Пример 4. Сторона треугольника равена: ( small a=7 ,) а прилежащие два угла равны соответственно ( small angle B=25°, ) ( small angle C=40°, ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Найдем, сначала, стороны b и c из формул (12),(13). Подставим значения ( small a=7 ,) ( small angle B=25°, ) ( small angle C=40°, ) в (12) и (13):
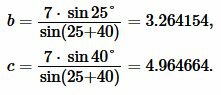 . . |
Далее найдем полупериметр p из формулы (14):
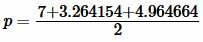 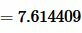 . . |
Подставляя значения a, b, c, p в (11), получим:
 |
Ответ:
Видео:№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать

math4school.ru
Видео:✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

Треугольники
Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Основные свойства

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
Внешним углом треугольника называется угол, смежный внутреннему углы треугольника.
Сумма углов треугольника равна 180°:
Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного:
Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол:

Средней линией треугольника называется отрезок, который соединяет середины двух его сторон.
Средняя линия треугольника параллельна одной из его сторон и равна её половине:
Видео:Геометрия - Построение правильного треугольникаСкачать

Равенство треугольников

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны:
У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)
В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.

Первый признак равенства треугольников.
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны:

Второй признак равенства треугольников.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны:

Третий признак равенства треугольников.
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны:
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Подобие треугольников

Подобными называются треугольники, у которых соответствующие стороны пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия:
Два треугольника подобны, если:
- Два угла одного треугольника равны двум углам другого треугольника.
- Две стороны одного треугольника пропорциональны двум сторонам другого, и углы, образованные этими сторонами, равны.
- Стороны одного треугольника пропорциональны сторонам другого.
У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны:
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному:

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:
Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Медианы треугольника

Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника.
- Три медианы треугольника делят его на шесть равновеликих треугольников:

Длины медиан, проведённых к соответствующим сторонам треугольника, равны:
Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Биссектрисы треугольника

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.
Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:
Длина биссектрисы угла А :

Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.
Биссектриса внешнего угла треугольника делит (внешне) противолежащую сторону на отрезки, пропорциональные двум другим сторонам.
BL – биссектриса угла В ;
ВЕ – биссектриса внешнего угла СВК :
Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Высоты треугольника

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Высоты треугольника обратно пропорциональны его сторонам:
Длина высоты, проведённой к стороне а :
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Серединные перпендикуляры

Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней.
Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника.
Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника.
Видео:№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Окружность, вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех его сторон.
Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков:
Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:
Видео:4K Как вписать окружность в треугольник, inscribed circle for triangleСкачать
Окружность, описанная около треугольника

Окружность называется описанной около треугольника, если она проходит через все его вершины.
Радиус описанной окружности:
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Расположение центра описанной окружности



Равнобедренный треугольник

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C.
В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота.

Основные формулы для равнобедренного треугольника:
Равносторонний треугольник

Треугольник у которого все стороны равны называется равносторонним или правильным треугольником.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Все углы равностороннего треугольника равны:

Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой, которые проведены из той же вершины:
Основные соотношения для элементов равностороннего треугольника
Прямоугольный треугольник

Треугольник называется прямоугольным, если у него есть прямой угол.
Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Прямоугольные треугольники равны если у них равны:
- два катета;
- катет и гипотенуза;
- катет и прилежащий острый угол;
- катет и противолежащий острый угол;
- гипотенуза и острый угол.
- одному острому углу;
- из пропорциональности двух катетов;
- из пропорциональности катета и гипотенузы.

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу:
Медиана, проведённая из вершины прямого угла, равна половине гипотенузы:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному:
Площадь прямоугольного треугольника можно определить
через катеты:
через катет и острый угол:
через гипотенузу и острый угол:

Центр описанной окружности совпадает с серединой гипотенузы.
Радиус описанной окружности:

Радиус вписанной окружности:
Вневписанные окружности

Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными.
Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.
Так точка О1 , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО1 и C О1 внешних углов Δ ABC при вершинах B и C .
Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей.
Δ ABC является ортоцентричным в Δ О1О2О3 (точки A , B и C – основания высот в Δ О1О2О3 ).
В Δ ABC углы равны 180°–2 О1 , 180°–2 О2 , 180°–2 О3 .
Радиус окружности, описанной около Δ О1О2О3 , равен 2 R , где R – радиус окружности, описанной около Δ ABC .
Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О1О2О3 .
Если ra , rb , rс – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно:
для r –
для R –
для S –
для самих ra , rb , rс –
Теоремы синусов, косинусов, тангенсов; формулы Мольвейде

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
- если c 2 > a 2 +b 2 , то угол γ – тупой ( cos γ
- если c 2 2 +b 2 , то угол γ – острый ( cos γ > 0 );
- если c 2 = a 2 +b 2 , то угол γ – прямой ( cos γ = 0 ).
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
Теорема тангенсов (формула Региомонтана):