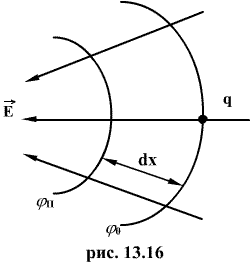
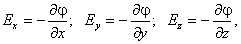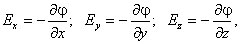Из выше сказанного следует, что электрическое поле характеризуется двумя физическими величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика). Выясним как они связаны между собой. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал 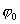
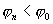
Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения 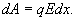
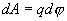
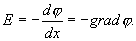 | (13.22) |
Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.
Для установления связи между силовой характеристикой электрического поля —напряжённостью и его энергетической характеристикой — потенциаломрассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q Edl, эта же работа равна убыли потенциальной энергии заряда q: dA = — dWп = — q d 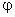
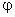
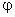
Ex dx + Ey dy + Ez dz = -d 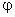
где Ex, Ey, Ez — проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем
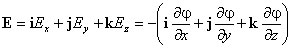
Стоящее в скобках выражение является градиентом потенциала j, т. е.
E= — grad 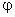
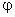
Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность Eнаправлена в сторону убывания потенциала.
Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен 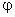
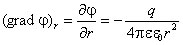
Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна
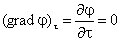
т. е. в этом направлении потенциал электрического поля является постоянной величиной ( 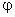
В рассмотренном случае направление вектора rсовпадает с направлением 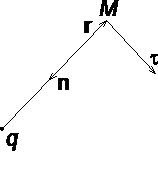
рис. 1.6
силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.
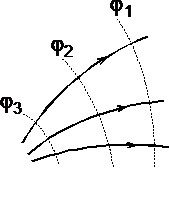
рис. 1.7
При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали — штриховыми.
Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.
| | | следующая лекция ==> | |
| ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА | | | Предел числовой последовательности |
Дата добавления: 2016-01-29 ; просмотров: 3714 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Вектор ex ey ez
Для установления связи между силовой характеристикой электрического поля — напряжённостью и его энергетической характеристикой — потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: d A = q E d l, эта же работа равна убыли потенциальной энергии заряда q: d A = — d W п = — q d 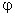
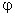
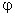
Ex d x + Ey d y + Ez d z = — d 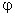
где Ex, Ey, Ez — проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем
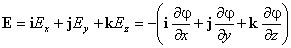
Стоящее в скобках выражение является градиентом потенциала j , т. е.
E = — grad 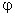
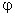
Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.
Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен 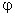
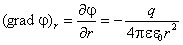
Проекция же градиента потенциала на направление вектора t , перпендикулярного вектору r, равна
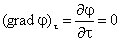
т. е. в этом направлении потенциал электрического поля является постоянной величиной ( 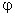
В рассмотренном случае направление вектора r совпадает с направлением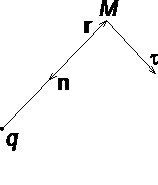
рис. 1.6
силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.
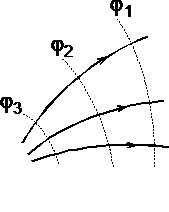
рис. 1.7
При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали — штриховыми.
Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.
1) Какова связь между напряженностью и потенциалом. Выведите ее и объясните.
2) Электростатическое поле имеет вид Е = a i + b j , где a и b константы. Является ли поле однородным. Написать выражение для потенциала поля.
3) Потенциал некоторого электростатического поля имеет вид 
4) Чему равна работа по перемещению заряда вдоль эквипотенциальной поверхности
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вектор ex ey ez
2.1. Основы прочностного анализа
Описание: В этом разделе рассмотрены физические соотношения для материалов с линейными свойствами.
где = ësxsyszsxysyzsxzû Т — вектор напряжений (как выходная величина помечается меткой S);
[D] – матрица упругости (описывается уравнениями (2.1-18) … (2.1-23), обратная матрица записывается в виде (2.1-4) и (2.1-5); для некоторых анизотропных элементов эта матрица вводится командами TBDATAс опцией TB,ANEL.);
– вектор температурной деформации (определяется соотношением (2.1-3), выходной массив EPTH).
Выходная величина EPEL представляет собой вектор деформаций, которые вызывают напряжения, т.е. – .
Замечание: в постпроцессоре POST1 подобная же величина EPTO, именуемая «компонентом суммарной деформацмм (component total strain)», может использоваться для маркировки оси деформаций при построении нелинейных кривых «s-e”. Составляющие приведенного выше вектора полной деформации можно трактовать как деформации, которые измеряются соответствующим датчиком. Эти два «полных» набора деформаций отличаются наличием или отсутствием вектора температурной деформации.
Компоненты вектора напряжений показаны на Рис. 2.1-1. Для используемых в программе ANSYS напряжений и деформаций принято следующее правило знаков: величины, относящиеся к растяжению являются положительными, к сжатию — отрицательными. Компоненты сдвига считаются положительными, если их направления совпадают с направлениями соответствующих координатных осей. Деформации сдвига представляют собой инженерные деформации, а не компоненты тензора.
Рис. 2.1-1. Компоненты вектора напряжений
Уравнение (2.1-1) может быть обращено следующим образом:
Для трехмерного случая вектор температурных деформаций определяется в виде соотношения
где ax – коэффициент температурного расширения в направлении оси х (вводится в виде параметра ALPX командойМР),
T – текущая температура в интересующей точке,
TREF – температура, при которой деформации отсутствуют (вводится командой TREF).
Матрица [D] -1 , нормализованная по столбцам, имеет вид:
Если используется нормализация по сторокам, то эта матрица записывается следующим образом:
Для записи элементов этих матриц используются обозначения:
Ex – модуль Юнга в направлении оси х (вводится как параметр ЕХ командой МР),
nxy – минимальный коэффициент Пуассона (вводится как параметр NUXY
n*xy– максимальный коэффициент Пуассона (вводится как параметр PRXY
Gxy – модуль сдвига в плоскости х-у (вводится как параметр GXY командой МР).
Матрица [D] -1 должна быть положительно определенной (см. раздел 13.5). Кроме того, эта матрица должна быть симметричной, поэтому для ортотропных материалов предполагается существование соотношений:
Согласно приведенным выше соотношениям, величины nxy, nzy, nzx, n*yx, n*zy иn*zx являются зависимыми и поэтому не задаются при вводе исходных данных.
Использование конкретных значений для коэффициентов Пуассона при анализе ортотропных материалов иногда приводит к затруднениям, поэтому к этому следует подходить с осторожностью. Обычно для ортотропных материалов бывают известны значения n*ху, или главного коэффициента Пуассона (PRXY). Величина n*хусчитается главным коэффициентом Пуассона, поскольку это значение больше, чем nху, если исходить из того, что Eх превосходит Eу.
Для упрощения в остальной части этого раздела будут использоваться только параметры nxy, nzy, nzx. Для изотропных материалов выполняются условия Eх = Ey = Ez и nxy = nzy = nzx, поэтому ввод исходных данных не вызывает затруднений. Для ортотропных материалов требуется проверять соответствие приведенных в справочной литературе данных требуемому формату ввода.
Если переписать равенство (2.1-2) в развернутом виде, используя выражения (2.1-3), (2.1-4), а также (2.1-6) . (2.1-8), то получим шесть уравнений:
где ex — деформация в направлении оси х,
exy — деформация сдвига в плоскости х — у,
sx — напряжения в направлении оси х,
sxy — напряжения сдвига в плоскости х — у;
компоненты с другими индексами получаются циклическим сдвигом (x — y- z).
С другой стороны, уравнение (2.1-1) можно переписать в развернутом виде, используя обратную матрицу (2.1-4), что вместе с уравнениями (2.1-3), (2.1-6) . (2.1-8) дает шесть соотношений для напряжений:
Если модули сдвига Gxy, Gyz, Gxz не задаются при вводе, то их значения вычисляются следующим образом:
Такие значения используются по умолчанию и предназначены только для изотропных материалов, поэтому при задании свойств ортотропных материалов пользователь должен убедиться, что справочное пособие по свойствам материала содержит нужное значение модуля сдвига.
Матрица [D] должна быть положительно определенной. Программа проверяет значение каждого задаваемого параметра материала, чтобы гарантировать положительную определенность этой матрицы. В случае зависящих от температуры свойств материала такая проверка выполняется при одинаковой температуре (командаBFUNIF) на первом шаге нагружения. Если материал изотропный или nxy, ny и nxz равны нулю, то матрица [D] будет всегда положительно определенной. Примером материала, нарушающим положительную определенность матрицы [D], служит материал, для которого выполняется условие Eу£ Eх(nxy) 2 .
2.1.2. Задание ортотропных свойств для осесимметричной модели
Преобразование параметров материала для расчетной модели, заданной в цилиндрической системе координат R-q-Z, в декартову систему x-у-z, в которой программой ANSYS предусмотрен ввод исходных данных, требует осторожности. Преобразование модуля Юнга выполняется однозначно, тогда как правильный способ преобразования коэффициента Пуассона не столь очевиден. Рассмотрим сначала, как преобразуется модуль Юнга из глобальной цилиндрической системы в глобальную декартову систему при использовании осесимметричных элементов для расчетной модели в виде диска:
как осесимметричный элемент
Рис. 2.1-2. Системы координат для материалов
Нетрудно видеть, что преобразование состоит в замене: ER ® Ex, Eq ® Ez и Ez ® Eу. В программе ANSYS ввод коэффициентов Пуассона, снабженных метками NUXY, NUYZ, NUXZ, осуществляется в глобальной декартовой системе координат соответственно для направлений x — y — z с помощью команды МР, после чего создается следующая согласованная матрица для нормальных напряжений, нормализованная по столбцам:
🎦 Видео
Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Единичный векторСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Орт вектора. Нормировать вектор. Найти единичный векторСкачать

2 37 Нахождение орта вектораСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Векторы в физике. Что нужно знать? | 50 уроков физики (2/50)Скачать

Найдите разложение вектора по векторам (базису)Скачать

Собственные векторы и собственные значенияСкачать

№757. Начертите векторы х, у и z так, чтобы x↑↑y, x↑↓z . Постройте векторыСкачать
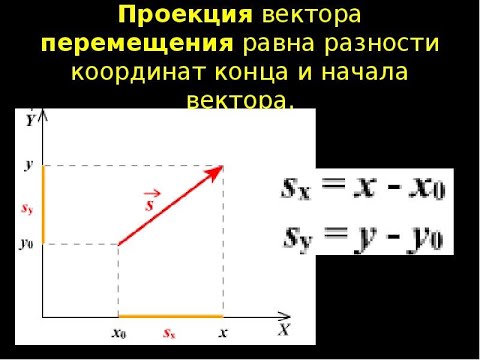
Вектор перемещенияСкачать
Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Физика | Ликбез по векторамСкачать

The electric field components in Fig are Ex=αx1/2,Ey=Ez=0 in which α=800N/C−m1/2. Consider the cubeСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Векторное произведение векторовСкачать