Треугольник вращается вокруг прямой параллельной меньшей стороне

Тело вращения представляет из себя цилиндр с высотой, равной меньшей стороне треугольника 13 см и радиусом оснований 16 см, из которого «вырезаны» усеченные конусы с равными радиусами и образующими 14 см и 15 см.

Искомая площадь — сумма боковых поверхностей этих усеченных конусов S1+S2 и боковой поверхности цилиндра S3.

а) Для решения нужно найти радиус меньшей окружности, которая образуется при вращении вершины треугольника, противолежащей меньшей стороне.

Найдем высоту треугольника, проведенную к меньшей стороне, из его площади. Площадь треугольника со сторонами 13,14,15 встречается часто и равна 84 ( проверьте по ф.Герона)

Высота равна 168:13= см

Радиус меньшей окружности равен R-h

≈3,0769 см

Формула боковой поверхности усеченного конуса

S1=π•14•(16+3,0769)= 267,0766π см ²

S2=π•15•(16+3,0769)=286,1535π см²

По формуле боковой поверхности цилиндра

S3=2πr•13=32•π•13=416π см²

S=969,2301π см² или ≈ 3044,926 см²

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Объем тел вращения 11 класс

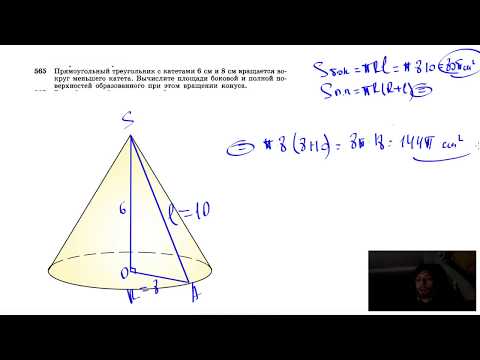
Видео:№565. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

ЗАДАЧА № 1. Равнобочная трапеция с основаниями 5 и 11 см и высотой 4 см вращается около большего основания. Найдите объем тела вращения. R 5см 4см 3см

ЗАДАЧА № 2. Правильный треугольник со стороной 4 см вращается около оси, проведенной через вершину параллельно стороне, не про- ходящей через эту вершину. Найдите объем тела вращения. R 4см 2см

ЗАДАЧА № 3. Прямоугольный треугольник с катетами 3 и 4 см враща-ется около прямой, параллельной меньшему из катетов и проходя-щей через вершину меньшего из углов треугольника. Найдите объем тела вращения. 4см 3см

ЗАДАЧА № 4. Прямоугольная трапеция с основаниями 10 и 18 см и высотой 6 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Найдите объем тела вращения. 6см 10см 18см

ЗАДАЧА № 5. Ромб со стороной 10 см и острым углом 60° вращается около стороны. Найдите объем тела вращения. 10см 60°

ЗАДАЧА № 6. Прямоугольный треугольник с катетом 3 см и гипотену-зой 6 см вращается вокруг оси, проходящей через вершину прямого угла параллельно гипотенузе. Найдите объем тела вращения. 6см hc 30° Vт.вр = R2 Н — ⅓R2 Н, Vт.вр = ⅔R2 Н. 3см

ЗАДАЧА № 7. Квадрат со стороной 8 см вращается около прямой, проведенной через вершину параллельно диагонали, не проходящей через эту вершину. Найдите объем тела вращения. ; ;

ЗАДАЧА № 8. Равнобедренный треугольник, угол при вершине которого равен , а боковая сторона равна m, вращается вокруг оси, содержащей боковую сторону. Найдите объем тела вращения. m 

ЗАДАЧА № 9. Прямоугольный треугольник площадью S и острым углом  вращается вокруг оси, проведенной через вершину прямого угла параллельно гипотенузе. Найдите объем тела вращения. С А В К тогда АС = Н cos, СK = Н sin cos Vт.вр = R2 Н — ⅓R2 Н, Vт.вр = ⅔R2 Н.  СK = ½H sin 2, Т.к. дана площадь АВС, то S = ½RН, 2S= ½H sin 2 ·H, 2S = RH, 4S= H2 sin 2,

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 959 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 337 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Вечканова Ольга ВладимировнаНаписать 14557 22.11.2015

Номер материала: ДВ-178568

22.11.2015 327

22.11.2015 371

22.11.2015 472

22.11.2015 824

22.11.2015 2940

22.11.2015 684

22.11.2015 1327

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Урок 1 Предмет стереометрии. Аксиомы стереометрии (стр. 35 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

Домашнее задание: №№ 000, 569, 570.

Урок 8
ПЛОЩАДИ ПОВЕРХНОСТИ ТЕЛ ВРАЩЕНИЯ

Цель: сформировать навык решения задач по теме.

I. Сделать чертеж тел вращения.

1. Тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей гипотенузу.

2. Тело, полученное вращением прямоугольного треугольника вокруг прямой, проходящей через вершину острого угла, параллельно противолежащему катету.

3. Тело, полученное вращением равностороннего треугольника ABC вокруг прямой, проходящей через вершину A, перпендикулярно стороне AB.

4. Тело, полученное вращением равностороннего треугольника вокруг прямой, содержащей одну из сторон треугольника.

5. Тело, полученное вращением тупоугольного равнобедренного треугольника вокруг прямой, содержащей основание треугольника.

6. Тело, полученное вращением равностороннего треугольника вокруг прямой, проходящей через вершину треугольника параллельно противолежащей стороне.

7. Тело, полученное вращением прямоугольного треугольника вокруг прямой, проходящей через вершину острого угла перпендикулярно гипотенузе.

8. Тело, полученное вращением прямоугольной трапеции вокруг прямой, содержащей меньшую боковую сторону.

9. Тело, полученное вращением прямоугольной трапеции вокруг прямой, содержащей меньшее основание.

10. Тело, полученное вращением прямоугольной трапеции вокруг прямой, содержащей большее основание.

11. Тело, полученное вращением равнобедренной трапеции вокруг прямой, содержащей меньшее основание.

12. Тело, полученное вращением равнобедренной трапеции вокруг прямой, содержащей большее основание.

13. Тело, полученное вращением ромба вокруг прямой, содержащей сторону ромба.

14. Тело, полученное вращением ромба вокруг прямой, проходящей через вершину ромба параллельно одной из диагоналей.

II. Решение задач.

Использовать сделанные чертежи.

1. Прямоугольный треугольник с катетом 8 см и прилежащим к нему углом 30° вращается вокруг прямой, содержащей гипотенузу. Найдите площадь поверхности полученного тела.

2. Равнобедренный треугольник, у которого боковые стороны равны по 4 см, а один из углов 120°, вращается вокруг прямой, содержащей большую сторону. Найдите площадь поверхности полученного тела.

3. В равнобедренной трапеции основания равны 14 и 50 см, а диагональ 40 см. Эта трапеция вращается вокруг прямой, содержащей меньшее основание трапеции. Найдите площадь поверхности полученного тела.

4. Диагонали ромба равны 6 и 8 см. Этот ромб вращается вокруг прямой, содержащей одну из его сторон. Найдите площадь поверхности полученного тела.

5. Треугольник со сторонами 25, 17 и 28 см вращается вокруг прямой, параллельной меньшей стороне и удаленной от нее на 20 см. Найдите площадь поверхности полученного тела, если ось вращения и вершина, противолежащая меньшей стороне, лежат по разные стороны от прямой, содержащей эту сторону.

6. Треугольник со сторонами 13, 14 и 15 см вращается вокруг прямой, параллельной меньшей стороне и удаленной от нее на 16 см. Найдите площадь поверхности полученного тела, если вершина, противолежащая меньшей стороне, лежит между осью вращения и прямой, содержащей эту сторону.

Домашнее задание: №№ 000, 546, 565, 566, 571, 615, 616. Придумать условие задач для неиспользованных чертежей.

Урок 9
СФЕРА И ШАР. УРАВНЕНИЕ СФЕРЫ. ВЗАИМНОЕ
РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ. КАСАТЕЛЬНАЯ
ПЛОСКОСТЬ К СФЕРЕ. ПЛОЩАДЬ СФЕРЫ

Цели: ввести понятия сферы и шара; вывести уравнение сферы; рассмотреть взаимное расположение сферы и плоскости; дать определение касательной плоскости к сфере; записать формулу для вычисления площади сферы.

I. Объяснение нового материала построить лекционным способом в соответствии с п. 64 – 68 учебника.

Для примеров используйте задачи: № 000 для уяснения определений сферы; № 000, 578 для отработки уравнения сферы; № 000 для иллюстрации взаимного расположения сферы и плоскости; № 000 (а), 594 для отработки формулы площади сферы.

II. Решение задач.

а) Дано: A и B лежат на сфере, ,
AM = MB.

Доказать, что OM AB.

1. OA = OB = R Д AOB – равнобед-
ренный.

2.

№ 000 (а). (Используйте тот же чертеж.)

а) A (–2; 2; 0), N (5; 0; –1).

Написать уравнение сферы.

а)

г)

Дано: шар пересечен плоскостью,
OM = 9 дм, R = 41 дм.

1. Сечением является круг радиуса MB.

2. MB == 5 ∙ 2 ∙ 4 = 40 дм.

Домашнее задание: теория (п. 64–68), № 000 (б, в, г), 577 (б, в), 579 (б, в), 587, 595.

Урок 10
СФЕРА И ШАР. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
СФЕРЫ И ПЛОСКОСТИ. ПЛОЩАДЬ СФЕРЫ

Цель: сформулировать навык решения задач по теме.

I. Проверка домашнего задания (№№ 000, 595.)

II. Решение задач.

Дано: A, B и C лежат на сфере,
R = 13 см, AB = 6 см, BC = 8 см,
AC = 10 см.

Найти расстояние от O до (ABC).

1. – центр описанной около Д ABC окружности.

2. – середина гипотенузы AC.

3. OH – искомое расстояние. OH == 12 см.

Дано: M, N и P – лежат на сфере,
R = 5 см, AC = AB = 10 см, BC = 12 см.

Найти расстояние от O до (ABC).

1. OM AB, ON BC, OP AC по свойству касательных.

2. Так как апофемы пирамиды равны, то ее вершина проецируется в центр вписанной в основание окружности.

HN = MN = PH = r как радиус вписанной в треугольник окружности.

2. r = 3 см.

4. Д HON прямоугольный. OH == 4 см.

Дано: сфера пересечена плоскостью,
R = 2 см, б = 30°.

1. В сечении – окружность радиуса BM.

2. BM = OB ∙ cos б, BM =.

3. C = 2рф, C = 2р.

Дано: шар пересечен плоскостью, угол между секущей и касательной плоскостями равен ц, OM = R.

1. В сечении – круг радиуса MK.

2. MOK = ц по свойству углов со взаимно перпендикулярными сторонами.

3. MK = OM ∙ sin ц = R sin ц.

4. Sсеч = р ∙ R2 ∙ sin2ц.

Дано: сфера касается граней двугранного угла MAM = 120°, OM = a, OM AM, ON AN.

🎦 Видео

Задание 3 ЕГЭ по математике. Урок 41Скачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

ЕГЭ №14. Задачи по стереометрии. 10-11 класс | Математика TutorOnlineСкачать

В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Задача 6 №27827 ЕГЭ по математике. Урок 96Скачать

№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

Задача про соотношение сторон. Геометрия 7 класс.Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Объем тела вращенияСкачать

Геометрическое решение задачи из видео Бориса Трушина. Изогональное сопряжение.Педальный треугольникСкачать

№566. Равнобедренный треугольник, боковая сторона которого равна m, а угол при основании равен φСкачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать