Как сравнить отрезки треугольника (2 видео)

Сравнение отрезков

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:

Содержание

Метод наложения:
Измерение длин:
Геометрия. 7 класс
Сравнение и измерение углов и отрезков
Что такое равенство геометрических фигур
Как сравнить отрезки
Сравнение углов
Правила измерения отрезков и углов
Примеры решения задач
📹 Видео

Метод наложения:

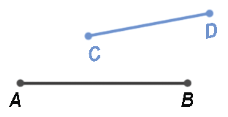
Пусть нам даны два отрезка AB и СD:

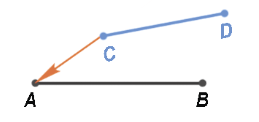
Совместим начало отрезка AB и СD (точки A и С).

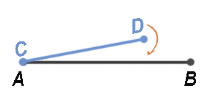
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

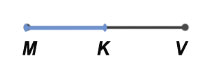
Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

MK = KV, K — середина отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

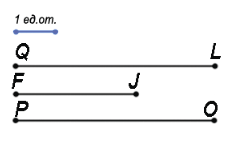
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

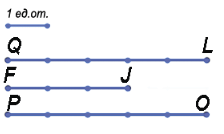
Наложим единичный отрезок на данные.

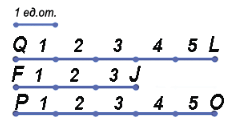
Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ

Если при наложении отрезков оба их концасовмещаются, значит отрезкиравны.
Если при измерении отрезков их длиныравны, то отрезки равны.

Поделись с друзьями в социальных сетях:

Видео:Математика 5 класс. Отрезок. Длина отрезка. Сравнение отрезков. Единицы измеренияСкачать

Геометрия. 7 класс

Конспект урока

Сравнение отрезков и углов

Перечень рассматриваемых вопросов:

Угол.
Луч.
Биссектриса угла.
Равные отрезки и углы.
Середина отрезка.

Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки и той точки, которая является началом луча.

Угол – часть плоскости, ограниченная двумя лучами с общим началом.

Стороны угла – лучи, из которых состоит угол

Середина отрезка – это точка, делящая его пополам, т.е. на два равных отрезка.

Две геометрические фигуры на плоскости называются равными, если их можно совместить наложением.

Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б.Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы.// Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

В окружающем нас мире очень много предметов, которые имеют одинаковую форму и размеры.

Например, два одинаковых мяча или две одинаковые тетради. Сегодня мы узнаем, как называются одинаковые геометрические фигуры, например, такие как отрезки и углы.

Для начала, рассмотрим, какие фигуры в геометрии называются равными.

Как установить, что плоские фигуры одинаковые?

Для этого существует способ наложения, опишем его.

Суть данного метода заключается в том, что если при наложении двух фигур друг на друга, они совместятся, то говорят, что первая фигура равна второй фигуре.

Т.е. две плоские геометрические фигуры называются равными, если их можно совместить наложением.

Так сравнивают отрезки и углы.

Для начала сравним отрезки.

Возьмём три отрезка АВ, CD и FE и сравним их между собой.

Чтобы установить, равны отрезки или нет, наложим один отрезок на другой так, чтобы один из концов отрезков совместился. Если при этом совместятся и другие концы, то отрезки будут считаться равными. Если два других конца не совместятся, то отрезки, соответственно, не будут между собой равны. При этом меньшим считается тот отрезок, который составляет часть другого.

В нашем случае отрезок АВ совместился с отрезком CD, следовательно, эти отрезки равны. А отрезок FE не совместился с отрезком АВ, следовательно, эти отрезки не равные, т.к. отрезок АВ составляет часть отрезка FE, то отрезок АВ будет меньше отрезка FE.

Аналогично можно сравнить отрезок CD с отрезком FE, отрезок FE не совместился с отрезком CD, следовательно, эти отрезки не равные, т.к. отрезок CD составляет часть отрезка FE, то отрезок CD будет меньше отрезка FE.

Видео:Геометрия 7 класс (Урок№3 - Сравнение отрезков и углов.)Скачать

Сравнение и измерение углов и отрезков

Видео:Как сравнивать отрезки? Геометрия 7 классСкачать

Что такое равенство геометрических фигур

Фигуры в геометрии называют равными, если в результате наложения они полностью совмещаются.

Другими словами, равные фигуры имеют одинаковые форму и размер.

Отрезок и угол — это геометрические фигуры, их сравнивают методом наложения.

Как сравнить отрезки

Сравнивая отрезки, совмещают конечные точки с одной стороны. Если другие концы отрезков также совместились, значит отрезки равны. На изображении отрезки АВ и СD равны. Это записывают как АВ=СD.

Если конечные точки не совместились — отрезки различаются по длине. Меньшим считается тот отрезок, который является частью большего. Ниже изображены отрезки, которые не равны, причем А 1 В 1 меньше С 1 D 1 . Кратко это пишут как А 1 В 1 ≠ С 1 D 1 , А 1 В 1 С 1 D 1 .

Сравнение углов

Чтобы сравнить углы, их также налаживают один на второй. При этом совмещают вершины и одну из сторон. Если другие стороны углов тоже совместились, значит углы равны. Совместим способом наложения углы АВС и DEF: они равны. ∠АВС=∠DEF.

Углы А 1 В 1 С 1 и D 1 E 1 F 1 не равны. Если совместить вершины В 1 и E 1 , а также стороны В 1 С 1 и E 1 F 1 , то стороны А 1 В 1 и D 1 E 1 не совместятся. Угол А 1 В 1 С 1 больше угла D 1 E 1 F 1 , так как ∠ D 1 E 1 F 1 входит в него и является его частью. ∠ А 1 В 1 С 1 ≠ ∠ D 1 E 1 F 1 , ∠ А 1 В 1 С 1 > ∠ D 1 E 1 F 1 .

Видео:Сравнение отрезков и угловСкачать

Правила измерения отрезков и углов

Длина — главное свойство отрезка. Длина выражается только положительным числом, то есть она всегда больше нуля.
Точка делит отрезок на две части. Длина целого отрезка равна сумме длин составляющих его отрезков.
Если три точки лежат на одной прямой, то одна из них расположена между двумя другими.
Из данной точки на прямой можно построить только по одному отрезку определенной длины в каждую сторону.
Основное свойство угла — градусная мера. Она всегда больше нуля.
Луч, проходящий между сторонами угла, разбивает его на два угла. Градусная мера угла равна сумме градусных мер углов, на которые он разбит лучом.
Развернутый угол — это угол, равный 180°.
От любого луча, лежащего на прямой, в заданной полуплоскости можно построить только один угол с заданной градусной мерой.

Видео:Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Примеры решения задач

Дано: точки K, M, N; длины отрезков KM=3 см, MN=4 см, KN=5 см.

Найти: находятся ли точки K, M, N на одной прямой.

Решение: если три точки лежат на одной прямой, то одна из них делит больший отрезок на два меньших, при этом длина большего отрезка равна сумме длин двух меньших отрезков. Больший отрезок — KN. Значит, если все три точки расположены на одной прямой, то точка М делит его на два отрезка KM и MN.

KN≠7 см, следовательно точки K, M, N не лежат на одной прямой.

Ответ: точки не лежат на одной прямой.

Дано: ∠ E F H = 90 0 . ∠ E F H разделен лучами ЕК и ЕМ на три равных угла.

Найти: угол между биссектрисами ∠EFК и ∠МFH.

Проведем построения. Пусть FO — биссектриса ∠EFК и FP — биссектриса ∠ М F H .
∠ E F К = ∠ К F М = ∠ М F H = ∠ E F H : 3 = 90 0 : 3 = 30 0 .
Так как ∠ E F К = ∠ М F H , т о ∠ О F К = ∠ Р F М = ∠ E F К : 2 = ∠ М F H : 2 = 30 0 : 2 = 15 0 .
∠ О F Р = ∠ О F К + ∠ К F М + ∠ Р F М = 30 0 + 15 0 + 15 0 = 60 0 .