Треугольник вписан в окружность радиуса 36 равен 30 (2 видео)

Треугольник вписан в окружность радиуса 36 равен 30

Задание 6. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30°. Найдите сторону AB этого треугольника.

Расширенная теорема синусов гласит, что

где a, b, c – соответствующие стороны треугольника; R – радиус описанной вокруг него окружности. Отсюда следует, что сторона AB, равна:

Содержание

За да ние Угол C треугольника ABC, вписанного в окружность радиуса 36, равен 30. Найдите сто ро ну AB этого тре уголь ни ка.
Треугольник вписанный в окружность
Определение
Формулы
Радиус вписанной окружности в треугольник
Радиус описанной окружности около треугольника
Площадь треугольника
Периметр треугольника
Сторона треугольника
Средняя линия треугольника
Высота треугольника
Свойства
Доказательство
🌟 Видео

Видео:2140 угол C треугольника ABC вписанного в окружность радиуса 10 равен 30 градусовСкачать

За да ние Угол C треугольника ABC, вписанного в окружность радиуса 36, равен 30. Найдите сто ро ну AB этого тре уголь ни ка.

Анфиса Докукина 2 лет назад Просмотров:

1 Вариант В тре уголь ни ке ABC угол C равен 90. Най ди те AB. За да ние Угол C треугольника ABC, вписанного в окружность радиуса 36, равен 30. Найдите сто ро ну AB этого тре уголь ни ка. За да ние Угол ACO равен. Его сторона C A касается окружности с центром в точке O. Сторона C O пересекает окружность в точках B и D (см. рис.). Найдите градусную меру дуги A D окружности, заключённой внутри этого угла. Ответ дайте в гра ду сах. 4. В па рал ле ло грам ме ABCD AB = 2, AD = 9,. Най ди те боль шую вы со ту па рал ле ло грам ма. 5. Один острый угол прямоугольного треугольника на 6 больше другого. Найдите больший острый угол. Ответ дайте в гра ду сах. За да ние За да ние За да ние Острые углы прямоугольного треугольника равны 24 и 66. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в граду сах /9

2 7. Най ди те сто ро ну квад ра та, опи сан но го около окруж но сти ра ди у са 25. За да ние В тре уголь ни ке ABC угол C равен 90, вы со та CH равна 8, BC = 16. Най ди те. За да ние В ту по уголь ном тре уголь ни ке, вы со та,. Най ди те. За да ние Боковая сторона равнобедренного треугольника равна 7, угол при вершине, противолежа щей ос но ва нию, равен 120. Най ди те диа метр опи сан ной окруж но сти этого тре уголь ни ка. За да ние В тре уголь ни ке угол равен 90, вы со та. Най ди те За да ние Най ди те синус угла. В от ве те ука жи те зна че ние си ну са, умно жен ное на. За да ние За да ние /9

3 13. Острые углы прямоугольного треугольника равны 85 и 5. Найдите угол между высо той и бис сек три сой, про ве ден ны ми из вер ши ны пря мо го угла. Ответ дайте в гра ду сах. 14. Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1 : 3 : 15 : 17. Най ди те угол A че ты рех уголь ни ка ABCD. Ответ дайте в гра ду сах. За да ние В тре уголь ни ке ABC угол C равен 90. Най ди те AC. За да ние В тре уголь ни ке ABC угол C равен 90,. Най ди те. За да ние В тре уголь ни ке ABC угол C равен 90,. Най ди те. За да ние У треугольника со сторонами 8 и 4 проведены высоты к этим сторонам. Высота, проведен ная к пер вой сто ро не, равна 1. Чему равна вы со та, про ве ден ная ко вто рой сто ро не? За да ние За да ние /9

4 19. В тупоугольном треугольнике, высота равна 20. Найдите. 20. Площадь треугольника ABC равна 4. D E средняя линия. Найдите площадь треуголь ни ка CDE. За да ние Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Най ди те пло щадь тра пе ции. За да ние В тре уголь ни ке угол равен 90. Най ди те. За да ние В тре уголь ни ке ABC угол C равен 90, CH вы со та. Най ди те AH. За да ние Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус ко то рой равен 6? За да ние В тре уголь ни ке ABC угол C равен 90,. Най ди те тан генс внеш не го угла при вер ши не B. За да ние /9

5 26. Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше дру гой. Най ди те мень шую сто ро ну па рал ле ло грам ма. За да ние В тре уголь ни ке ABC угол C равен 90. Най ди те. За да ние Меньшая сторона прямоугольника равна 20, диагонали пересекаются под углом 60. Най ди те диа го на ли пря мо уголь ни ка. За да ние В треугольнике угол равен 90,. Найдите косинус внешнего угла при вер ши не A. За да ние Отрезки AC и BD диаметры окружности с центром O. Угол ACB равен 38. Найдите угол AOD. Ответ дайте в гра ду сах. За да ние За да ние /9

6 31. Сто ро на AB треугольника ABC равна 7. Противолежащий ей угол C равен 150. Найди те ра ди ус окруж но сти, опи сан ной около этого тре уголь ни ка. 32. В тре уголь ни ке угол равен 90, угол равен,. Най ди те вы со ту. За да ние В тре уголь ни ке ABC угол C равен 90,. Най ди те. За да ние За да ние Сумма двух углов треугольника и внешнего угла к третьему равна 30. Найдите этот третий угол. Ответ дайте в гра ду сах. За да ние В тре уголь ни ке ABC угол C равен 90,. Най ди те. 36. В тре уголь ни ке ABC угол C равен 90, CH вы со та. Най ди те BH. За да ние За да ние /9

7 37. В тре уголь ни ке ABC угол C равен 90. Най ди те. 38. Найдите радиус окружности, описанной около треугольника, если стороны квадрат ных кле ток равны 1. В от ве те ука жи те. За да ние Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 60. Най ди те диа го на ли пря мо уголь ни ка. За да ние В прямоугольнике диагональ делит угол в отношении 1 : 2, меньшая его сторона равна 57. Най ди те диа го наль дан но го пря мо уголь ни ка. За да ние Най ди те ра ди ус окруж но сти, впи сан ной в квад рат со сто ро ной 56. За да ние За да ние Дуга окружности AC, не содержащая точки B, составляет. А дуга окружности BC, не содержащая точки A, со став ля ет. Най ди те впи сан ный угол ACB. Ответ дайте в гра ду сах. За да ние Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 70. Найдите боль шую сто ро ну па рал ле ло грам ма. За да ние /9

8 44. В тре уголь ни ке ABC AB = BC, AC = 8, вы со та CH равна 2. Най ди те синус угла ACB. 45. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Най ди те ра ди ус опи сан ной окруж но сти этого тре уголь ни ка. За да ние В тре уголь ни ке ABC угол C равен. Най ди те AC. За да ние Четырёхугольник ABCD вписан в окружность. Угол ABC равен 100, угол CAD равен 64. Най ди те угол ABD. Ответ дайте в гра ду сах. За да ние В тре уголь ни ке ABC AC = BC, вы со та СН равна 1, Най ди те АС. За да ние Най ди те сред нюю линию тра пе ции, если ее ос но ва ния равны 48 и 72. За да ние /9

9 50. В тре уголь ни ке угол равен 90, вы со та. Най ди те. За да ние За да ние /9

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Треугольник вписанный в окружность

Видео:Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

Высота треугольника вписанного в окружность,
если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Радиус описанной окружностиСкачать

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

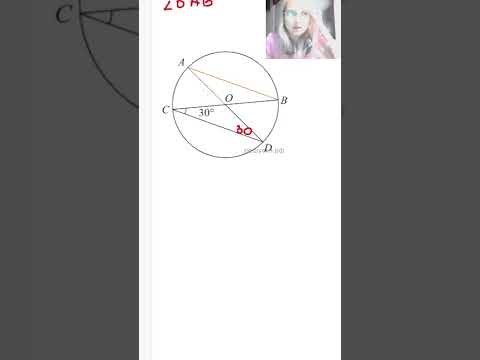
Видео:В окружности проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.