Как пересекаются параллельные прямые лобачевский доказал

Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.

Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.

И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.

Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.

Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского выглядит следующим образом:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.

Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.

Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.

В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».

Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».

Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:

x 2 + y 2 + z 2 = c 2 t 2 ,

при делении на t 2 , то есть для скорости света, даёт уравнение сферы в пространстве с координатами v_x, v_y, v_z, которые являются составляющими скорости света по осям х, у, z.

Преобразование Лоренца сохраняет эту сферу, а поскольку они линейны, переводят прямые пространства скоростей в прямые. Из этого следует, (согласно модели Клейна) что в пространстве скоростей внутри сферы радиуса с , значит есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Новое в блогах

Видео:24. Параллельные линии могут пересекаться. Такое возможно?Скачать

Пересекаются ли параллельные или Что говорил Лобачевский?

Недавно в посте на околонаучные темы один из комментаторов завел разговор о геометрии Лобачевского (что он ее не понимает) и даже вроде попросил объяснить. Я тогда ограничилась утверждением, что понимаю. Объяснять эту теорию в ограниченных рамках комментария и одним текстом (без рисунков) показалось мне невозможным.

Однако, подумав, я все же решила попробовать дать небольшой популярный экскурс в эту теорию.

Немного предыстории. Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких постулатов (аксиом). Считалось, что эти аксиомы «очевидны», т.е. отражают свойства реального (физического) пространства.

Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова:

«Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну-то прямую можно провести, является не аксиомой, а теоремой.

При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая – одна!

(Распространенное утверждение «Лобачевский доказал, что параллельные прямые могут и пересекаться» — конечно, является вопиюще неправильным! Ведь это бы противоречило их определению!)

Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он, как это часто делается в математике, выбрал метод «от противного», т.е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится! Т.е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование!

Конечно, в первое время его выкладки не признавали, смеялись над ним. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что ЧИСТО ЛОГИЧЕСКИ теория Лобачевского ничем не хуже евклидовой.

Один из остроумных способов убедиться в этом – придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один.

Пожалуй, самой простой является модель Пуанкаре. Вы можете сами построить ее нехитрыми приборами.

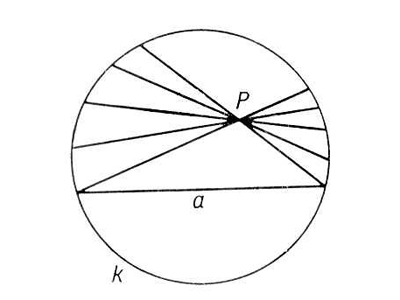
Начертите не листке бумаги прямую. Возьмите циркуль и, ставя его иглу на эту прямую, нарисуйте полуокружности, находящиеся с одной стороны от прямой. Теперь сотрите прямую (и с ней – концевые точки полуокружностей). Так вот, эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского!

Действительно, выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли) Т.е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их – бесконечное количество.

Можно заметить, что треугольники в этой модели не такие, как на плоскости (евклидовой): сумма их углов меньше 180 градусов! Впрочем, чем меньше треугольник, тем больше сумма его углов. В «малом», на небольших расстояниях, геометрия Лобачевского практически совпадает с геометрией Евклида. Поэтому, вообще говоря, мы не сможем «экспериментально» отличить одну от другой, если окажется, что доступные нам (космические) расстояния– малы для этой цели.

Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства. Математики поняли, что все, что они могут сказать: если верны такие-то аксиомы, то верны и такие-то теоремы. Ну, а что такое «множества», «точки», «прямые», «углы», «расстояния», и т.п. – этого мы не знаем! Прямо как у Станислава Лема: «Сепульки – это объекты для сепулькирования»

«Говорят, Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чем говорим, и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. [ … ] Таким образом, одна из главных функций математического доказательства – создание надежной основы для проникновения в суть вещей.»

Видео:Что на самом деле доказал Лобачевский?Скачать

Геометрия Лобачевского

Материал из Lurkmore

Геометрия Лобачевского (гиперболическая геометрия) — очень хитрое математическое колдунство по типу всем известной геометрии Евклида, но с небольшим отличием, делающим ее невозможной для понимания 95% населения.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Содержание

Видео:Неевклидова геометрия Лобачевского — Валентина КириченкоСкачать

[править] Суть

В геометрии Лобачевского вместо классического евклидового пятого постулата:

В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.

»— Евклид (точнее Прокл)

используется другая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её

»— Лобачевский

И что, сука, характерно — если рисовать прямые не на плоскости, а на гиперболоиде (ну например, на лошадином седле), то именно так всё и получится. Чем хороша такая аксиома, что тут вообще получается, как это всё, БЛДЖАД, получилось и вообще история вопроса — всё это будет рассмотрено ниже.

Видео:Неевклидова геометрия #shorts #nonEuclideangeometry #lobachevskyСкачать

[править] Аксиомы Евклида

[править] Евклид

Во времена древней Греции, помимо зайчатков всякой философии, были заложены и основы современной математики. Особо отличились здесь Евклид и Диофант. Про самого Евклида Александрийского, проживавшего в 3 веке до н. э., известно немного, однако главное, что он сделал — это запилил «Начала» — эпичный учебник по геометрии, в котором среди прочего была сформулирована система аксиом, которую с небольшими изменениями ажно до ХХ века использовали в геометрии как основную. А сами «Начала» считались главным и образцовым учебником по геометрии. Модернизация учебных курсов? Ну-ну…

[править] Аксиоматический метод

Немножко скукоты, без которой дальнейший рассказ не заладится. Что такое аксиомы и постулаты? Это утверждения, которые принимаются за данность. Система аксиом может быть противоречивой (плохая, негодная система) и непротиворечивой (хорошая, годная). При этом некоторые определения даются явно (например, окружность — это множество точек плоскости, равноудаленных от данной точки, называемой центром), а некоторые даются неявно. Например, точка — это объект, который удовлетворяет системе аксиом (то есть в другой системе аксиом, точнее в геометрической реализации, точкой может быть что-то не похожее на то, к чему мы привыкли).

Помимо системы аксиом, есть ещё модель (геометрическая реализация). То есть некий способ представления (визуализации) системы аксиом. К разным моделям геометрии Лобачевского мы ещё вернёмся, но пока отметим, что, когда школиё рисует чертежи, оно как раз таки и работает в данной геометрической реализации евклидовой геометрии. Другое дело, что в случае с евклидовой геометрией исторически сначала появилась геометрическая реализация (точки, отрезки, окружности), а потом под эту геометрическую реализацию была подогнана система аксиом. А в случае с геометрией Лобачевского было ровно наоборот.

Тащемта, аксиоматический метод состоит в том, что при изучении какой-нибудь области науки нужно сначала сформулировать необходимый набор аксиом, проверить их непротиворечивость, а потом в рамках выработанных правил работать. Границы применимости этого метода в своё время разработал Гёдель со своей теоремой Гёделя. Он, в частности, доказал, что конечная система аксиом не может быть полной (то есть в терминах данной аксиоматики всегда можно сформулировать утверждение, правильность которого нельзя проверить в данной системе аксиом). Для слабых разумом школьников отметим, что это отнюдь не «что-то плохое», во-первых, не факт, что «непроверяемое утверждение» — важное, а во-вторых, аксиоматика всё-таки получается обычно из конкретных задач, а значит, даже при отсутствии соответствующей аксиомы её всегда можно добавить. Пример такого утверждения в стандартной Евклидовой геометрии [1] — аксиома Паша. В общем, от непроверяемости некоторых утверждений ещё никто не умер (но кое-кто сошёл с ума).

Отметим, что в математике аксиоматический метод является основным. Но не только в математике. Например, этот ваш Ландафшиц состоит из аксиоматического метода (главная аксиома — это принцип наименьшего действия) чуть менее, чем полностью. Почему-то многие думают, что в арифметике аксиом нет, что, конечно, ЛПП — см. аксиомы Пеано.

Впрочем, аксиоматический метод не является в полном смысле панацеей. Им, как и любым другим инструментом, нужно пользоваться с умом. Дело тут, в частности, в парадоксах (например, парадоксы Зенона и парадокс брадобрея), которые кагбе демонстрируют внутреннюю противоречивость там, где её на самом деле нет. Дело в том, что некоторые парадоксы являются багами языка, на котором людишки общаются и пишут статьи. Так, например, в языке многие слова обладают разными значениями, и многое зависит от контекста: точка в физике и точка в математике — это совсем не одно и то же. С этой проблемой в теории можно справиться созданием научного новояза, но всем похуй.

Другая проблема состоит в том, что некоторые термины считаются в школьной литературе «очевидными», например, понятие множества. Точные и аккуратные определения существуют, но ни фига не являются простыми. Так что аккуратные системы аксиом могут оказаться несколько более громоздкими, чем хотелось бы. Разделы математики, которые занимаются (и вполне успешно, кстати) исправлением этих багов — это теория множеств (не та поебень с кружочками и точечками, которую ты в школе проходил) и математическая логика.

Видео:1. Лобачевский и его наследие. Основные постулаты геометрии.Скачать

[править] Что не так с пятым постулатом?

С исходным текстом «Начал» работать не очень удобно, поэтому будем действовать в рамках аксиом Гильберта. Проблема в том, что остальные аксиомы гораздо проще и интуитивно очевиднее. Например, вполне в духе КО: «Каковы бы ни были две точки A и B, существует прямая, которой принадлежат эти точки.» А вот пятый постулат выглядит как-то неочевидно и неестественно. Поэтому возникает естественное желание вывести его из других аксиом. Однако, почему-то ничего не получалось. Удаётся свести пятый постулат к другим утверждениям, которые выглядят совсем дико, но формального, строгого доказательства не существует. Вот несколько направлений, по которым пытались действовать предшественники Лобачевского.

[править] Четырехугольник Саккери

Четырёхугольник Саккери в естественной среде обитания

Четырёхугольник Ламберта, как он есть

Такой себе четырехугольник ABCD, в котором стороны AB и DC равны и перпендикулярны основанию AD. С точки зрения евклидовой геометрии (и с использованием пятого постулата) должен получиться прямоугольник. Однако без использования пятого постулата доказать это не удастся; можно доказать, что углы B и C одинаковые, но прямые ли они? Старина Саккери (а до него Омар Хайям) пытался рассмотреть альтернативные варианты: либо два оставшихся угла тупые, либо острые. Случай тупых углов худо-бедно ему изучить удалось, доказав, что так не бывает, но вот в случае острых углов — не удалось. Пичалько.

Алсо, у четырехугольника Саккери есть и «братец» — четырехугольник Ламберта, в котором 3 угла — прямые. Появился по тем же причинам и с тем же успехом.

[править] Сумма углов треугольника

Которая, как известно, 180˚. Впрочем, доказать это без использования пятого постулата тоже не получится. Вариант с суммой углов строго меньше 180˚ не противоречит другим аксиомам. Пример того, как тут можно лажануть, доставил Лежандр (между прочим, годнейший математик, а не какой-нибудь там фрик) в своей книжке «Начала геометрии». Самое рассуждение и разбор ошибки можно невозбранно посмотреть здесь [1].

[править] Бесподобное подобие

Очевидно, что если взять треугольник и увеличить его стороны одновременно в несколько (в одно и то же число) раз, то у полученного треугольника углы будут такие же, как у исходного. Ну и вообще, кажется вполне очевидным, что существуют подобные, но не равные треугольники (аксиома Валлиса). Очевидно, но неверно. Существование неравных подобных треугольников равносильно справедливости пятого постулата. Более того, в геометрии Лобачевского треугольник однозначно определяется своими углами. Пиздец? Да, пиздец как он есть. Но отсутствие различных подобных треугольников не противоречит аксиоматике, хотя и противоречит здравому смыслу (основанному на привычной нам геометрической реализации). Так что для геометрии Лобачевского нужно слегка расширить сознание…

[править] Пифагоровы штаны

Справедливость теоремы Пифагора для хотя бы одного прямоугольного треугольника вкупе с остальными аксиомами равносильна справедливости пятого постулата. А вот отсутствие пятого постулата херит теорему Пифагора и всю, блджад, классическую тригонометрию с синусами и косинусами. Так что без пятого постулата штанишки оказываются дырявыми.

Это значит, что если отказаться от пятого постулата, то рушится всё: формулы для расстояний, углов, площадей, признаки равенства и подобия, даже небо, даже Аллах…

[править] Теперь сходитесь!

Очевидно, что если две прямые сближаются (берём точку на одной прямой и опускаем перпендикуляр на другую), то они пересекаются. Очевидно, но опять же неверно. Потому что ниоткуда не следует, что если они начали сближаться, то они будут сближаться с равномерной скоростью, а значит не факт, что пересекутся. Это был ещё один способ доказать, что параллельная прямая уж если существует, то единственная. Но увы, не фартануло.

Было много других самых разных способов разобраться с пятым постулатом. Но всех исследователей ждал былинный отказ. Одни в результате признавали, что их рассуждения неполны, другие до конца жизни упорствовали. Многие допускали характерную ошибку, неявно используя то или иное утверждение, казавшееся им очевидным, но оказывавшимся на самом деле лишь эквивалентной формулировкой пятого постулата. Сколько пытливых ученых сбрендило? Сколько тысяч человеко-часов потрачено впустую? Кто знает.

Видео:НЕЕВКЛИДОВАЯ ГЕОМЕТРИЯ. оказывается это так просто...Скачать

[править] Драма

В начале XIX века общий уровень математики начал расти на глазах изумленной публики, переведя её из состояния «обобщим и углубим наследие великих древних греков» в состояние «давайте придумаем что-нибудь новое». Родился и активно развивался разнообразный матан, уже вполне напоминающий современный. Надо, впрочем, понимать, что как такового аксиоматического метода ещё не было, но появление его было неизбежно. И вот первопроходцем выступил Карл Фридрих «Король математиков» Гаусс.

[править] Гаусс

Дедушка Гаусс был дичайше крутым математиком. Он успел наследить повсюду: теория чисел, геодезия, геометрия, математический анализ, тысячи их. Конечно, не оставил он без внимания и пятый постулат. По всей видимости, он был первым, кто пришёл к мысли о том, что пятый постулат нельзя вывести из остальных аксиом, а главное, что в этом нет ничего плохого. Насколько глубоко и хорошо он разработал новую геометрию — непонятно, тем паче что Гаусс никогда не заявлял публично, что он тоже придумал неевклидову геометрию. Злые языки утверждают, что Гаусс опасался, что после публикации работ по неевклидовой геометрии все решат, что у дедушки началась деменция, или он просто поехавший. Так что Карл наш Фридрих Гаусс в данном вопросе ограничился ролью, столь близкой анонимусу, а именно ролью комментатора.

Но вот в конце двадцатых годов XIX века вокруг пятого постулата стало жарко.

[править] Лобачевский

Вообще-то Николай наш Иванович жизнь прожил долгую и насыщенную, а своим современникам был известен в первую очередь как хороший, годный ректор Казанского университета. Именно благодаря его мудрому руководству Казанский университет, который при Александре I чуть было не закрыли (это отдельный лулз, потому как гнобили Казанский университет за недостаточную духовность, например, за человеческие тушки на кафедре анатомии), стал в результате одним из лучших университетов ещё той страны. Впрочем, нас интересует в основном его деятельность в области неевклидовой геометрии. А вот тут на него современники смотрели как на говно.

В 1829 году (запомни эту дату, анон) вышла его первая работа по неевклидовой геометрии. Последнюю свою работу он уже слепой будет додиктовывать своим ученикам через 30 лет. Дядя Коля пришёл к тому же выводу, что и Гаусс. Он понял, что пятый постулат нельзя вывести из остальных аксиом, и начал разрабатывать аналитические методы в новой геометрии. Мы ведь помним, что без пятого постулата нет тригонометрии, правда? А без тригонометрии и теоремы Пифагора нельзя даже расстояние между точками посчитать, нельзя угол измерить. Именно созданием всех этих формул и занимался Лобачевский следующие несколько десятилетий, регулярно получая лучи поноса в свой адрес от самых разных математиков. С учётом того, что у Иваныча не было геометрической модели, всю науку он строил без чертежей чисто аналитически, что было ниибацо сложно и абсолютно непонятно для окружающих.

Собственно, оценили работы Иваныча из современников только двое. Это был, во-первых, Гаусс, который дичайше котировал работы Лобачевского и писал об этом коллегам, но, сука, не написал об этом Лобачевскому и никогда публично ни единым словечком не поддержал его. Вторым понявшим был расовый венгр Бойяи, к которому мы вернёмся чуть ниже. А пока остановимся на том, какую травлю получил за свою геометрию Лобачевский при жизни.

О том, что я прочёл, я считаю долгом сообщить Академии: 1) Из двух определённых интегралов, которые г–н Лобачевский считает своим открытием, один уже известен. Его можно получить на основании самых элементарных принципов интегрального исчисления. Значение другого интеграла, данное на стр. 120, является, поистине, новым. Оно — достояние г–на Казанского ректора. К несчастью, оно неверно [2] . 2) Всё, что я понял в геометрии г–на Лобачевского, ниже посредственного. 3) Всё, что я не понял, было, по-видимому, плохо изложено по той же самой причине, что в нём трудно разобраться. Из этого я вывел заключение, что книга г–на ректора Лобачевского опорочена ошибкой, что она небрежно изложена и что, следовательно, она не заслуживает внимания Академии.

»— Остроградский

Надо понимать, что Остроградский — это не какой-нибудь там фрик, а хороший, годный и уважаемый учёный. А вот анонимы писали и похлеще:

Даже трудно было бы понять и то, каким образом г. Лобачевский из самой легкой и самой ясной в математике, какова геометрия, мог сделать такое тяжелое, такое темное и непроницаемое учение, если бы сам он отчасти не надоумил нас, сказав, что его Геометрия отлична, от употребительной, которой все мы учились и которой, вероятно, уже разучиться не можем, а есть только воображаемая. Да, теперь все очень понятно. Чего не может представить воображение, особливо живое и вместе уродливое!

»— из анонимной статьи в журнале «Сын отечества»

И все 30 лет, что Лобачевский прожил в статусе создателя неевклидовой геометрии имени себя, никак, кроме как «говном», его геометрию не называли. Даже его собственные ученики, которые после того, как Николай Иваныч ослеп, записывали под его диктовку его последнюю книгу «Пангеометрия», считали его поехавшим старым козлом и не стеснялись в выражениях. А ты бы смог пережить такую травлю, анон?

[править] Бойяи

Бойяи-отец недоволен деятельностью сыночка

Бойяи-сын бородат и постулат

Ты должен бросить это как самое гнусное извращение. Оно может отнять у тебя всё время, здоровье, разум, все радости жизни. Эта чёрная пропасть в состоянии, может быть, поглотить тысячу таких титанов, как Ньютон…

»— Бойяи старший намекает младшему

Бойяи-отец Фаркош был неплохим по своим временам математиком, водил дружбу с упомянутым уже Гауссом. Он, среди прочего, занимался пятым постулатом и изрядно подсел на оный. И немало огорчился, когда узнал, что его сын Янош тоже занялся этим безблагодатным делом. Он просил сыночку не заниматься этой хуитой, подчеркивая полную безблагодатность этого дела. Но Янош Фаркошевич папу не послушался. Мозг молодого Бойяи оказался куда как более подвижным, чем у папы, и он… повторил выводы Гаусса и Лобачевского. Подготовленная работа была опубликована в качестве приложения (Appendix) к работе папы Фаркоша в 1832 году. Спустя всего лишь 3 года после работы Лобачевского. Три года на фоне двух тыщ лет, которые стояла проблема! Гаусс написал письмо старшему Бойяи, в котором весьма лестно отозвался о работе младшего Бойяи, но отметил, что уже видел нечто похожее в работе одного русского…

Бойяи-сын, мягко говоря, прихуел, выучил русский язык чтобы прочитать работы Лобачевского в оригинале, и… охуел окончательно. Ходят слухи, что он даже подозревал Лобачевского в том, что тот спёр у него результат, и на почве расстройства съехал крышей. Ни одной работы по математике он больше так и не опубликовал, но сохранилось, если верить загнивающей, 20 000 листов черновиков по разным математическим темам.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

[править] Матчасть

На выходе у Лобачевского получилось вот что. Есть система аксиом, есть проработанный матан для новой геометрии, причём матан ужас какой сложный и непонятный. И ни одной понятной картинки. А, главное, непонятно, как объяснить, что новая система аксиом непротиворечива. Из полученных адовых формул совершенно не следует, что где-то там впереди за новым поворотом не появится какого-нибудь противоречия. Ну и, самое главное, современникам непонятно, нахуя весь этот огород городить!

Ясность внёс макаронник Бельтрами, который предложил три геометрические модели, которые реализовывали геометрию Лобачевского. Если попросту, то если назвать одни объекты прямыми, а другие точками получалось нечто, достаточно естественное с одной стороны, а, главное, в новой модели выполнялись аксиомы геометрии Лобачевского. То есть новая геометрия описывала не какую-то неведомую ёбаную хуйню, а вполне понятный объект, доступный для понимания простому смертному. Моделей Бельтрами предложил несколько, самые известные из них называются, в соответствии с принципом Арнольда, именами Пуанкаре и Клейна. Хорошо написано про них, например, здесь, а мы коротенько распишем одну из них. А именно модель Пуанкаре в верхней полуплоскости.

[править] Модель Пуанкаре

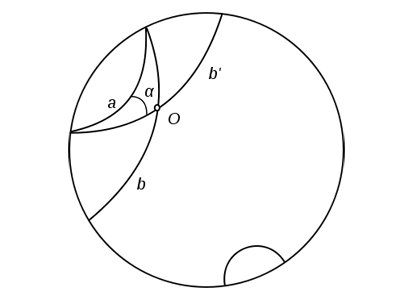
f — абсолют, a, b — «прямые». Соответственно одна из них полуокружность, а вторая — луч, перпендикулярный абсолюту.

«треугольники» в геометрии Лобачевского, выделены жирным

«углы» между «прямыми» в геометрии Лобачевского это углы между касательными в точке пересечения

Возьмём на плоскости прямую, которую называют абсолютом. Чтобы не путаться, в кавычках будут новые объекты в геометрии Лобачевского. Назовём «плоскостью» верхнюю полуплоскость (абсолют не включаем), «прямыми» — полуокружности, лежащие в «плоскости», у которых центр на абсолюте и лучи, перпендикулярные к абсолюту. «Точками» назовём обычные точки в верхней полуплоскости. «Углом» будем называть угол между касательными к «прямым» в точке пересечения. Из картинки видно, что из данной «точки», не лежащей на данной «прямой», действительно можно провести две (и даже бесконечно много) «прямых», которые не пересекаются с данной. Остальные аксиомы, которые есть в евклидовой геометрии, выполняются, что легко проверить даже школьнику. Единственная трудность в том, что новые «объекты» отличаются от привычных нам. Но, с другой стороны, и что дальше? Аксиомы-то выполняются! А значит, непротиворечивость геометрии Лобачевского равносильна непротиворечивости геометрии Евклида.

В новой геометрии есть и своя «тригонометрия», в которой в роли тригонометрических функций выступают так называемые гиперболические функции. Но про это уже читайте в спец. литературе.

[править] Особенности геометрии Лобачевского

Тут вам не учебник, но кое-что нужно отметить для полноты картины. Ибо нужно понимать, что от замены одной аксиомы меняется, сцуко, очень многое. И, что важно, интуиция, которая работает в евклидовой геометрии и к которой мы привыкли, перестаёт работать в гиперболическом мире. Понять это без геометрической модели очень сложно, так что остаётся только восхититься Николаем Иванычем, который вот это всё понял и не зассал опубликовать.

• Сумма углов — строго меньше православных 180˚. А разница между суммой углов и 180 — это число, называемое дефектом, и оно пропорционально площади.
• Признак равенства по трём углам — что дико доставляет, в геометрии Лобачевского нет неравных подобных треугольников, а, значит, любой треугольник однозначно определяется набором углов.
• Медианы пересекаются в одной точке — таки да, хотя для доказательства в евклидовой геометрии обязателен пятый постулат. Но, оказывается, при наличии отрицания пятого постулата они всё равно пересекаются в одной точке. Не пытайтесь повторить это в домашних условиях…
• Окружность. В упомянутой модели Пуанкаре «окружности» — это внезапно окружности (евклидовы), у которых «центр» находится не в центре. Нутыпонел.
• Тригонометрия. Уся тригонометрия там имеется, включая теоремы косинусов и синусов. Только синусы и косинусы там гиперболические, а формулы хоть и похожи, но всё-таки другие. Вот кое-что
• Паркет Лобачевского. Плоскость, как известно, можно покрыть одинаковыми правильными треугольниками, четырехугольниками и шестиугольниками. А вот в геометрии Лобачевского всё гораздо интереснее: там есть покрытия плоскости одинаковыми правильными многоугольниками из любого количества вершин. Так-то!

Видео:Мнимая ошибка, над которой ломали голову 2 000 лет [Veritasium]Скачать

[править] Братишки

Ну вот худо-бедно мы выяснили, что геометрий есть, по крайней мере, две — Евклидова и геометрия Лобачевского. Конечно, это не всё, ведь систему аксиом можно выбирать какую угодно. Но выбирают системы аксиом в современном мире обычно исходя из того, какую именно задачу нужно решать в данный момент. То есть, как правило, в интересной геометрической модели выбирают, что назвать прямыми, точками, и т. п., а потом выясняют, каким аксиомам они удовлетворяют. Перечислим тут несколько примеров.

• Сферическая геометрия — в известном смысле самая первая неевклидова геометрия, которой занимались задолго до того, как это стало мейнстримом. Но не вполне понимали, чем именно занимаются. Плоскость — это сама сфера, прямые — большие окружности, у которых центр совпадает с центром сферы. Отличается от евклидовой геометрии не только пятым постулатом (здесь вообще нет параллельных прямых), но и некоторыми другими. В этой геометрии сумма углов треугольника всегда больше 180˚, и существует треугольник, у которого все углы прямые.
• Абсолютная геометрия — геометрия, в которой вообще нет пятого постулата. Хороша тем, что утверждение, доказанное в ней, будет справедливо и для евклидовой геометрии, и для гиперболической. Но доказать большинство утверждений в ней сложновато.
• Риманова геометрия — антипод геометрии Лобачевского. Здесь на месте пятого постулата стоит аксиома, гласящая, что любые две прямые пересекаются. Тоже достаточно важная штука, играет большую роль в современной дифференциальной геометрии. В качестве модели может служить евклидова плоскость, к которой добавили одну точку, типа «бесконечность», в которой пересекаются параллельные прямые. Близким (но не тем же самым!) понятием является так называемая проективная геометрия. Последняя играет важную роль, например, для этих ваших художников при рисовании эпических полотен. Ты же знаешь, что такое перспектива, мой художественный друг?
• Пространство Минковского — про это написано на уютненьком в соответствующем месте.
• Общая теория относительности — тоже живёт в неевклидовом пространстве. Только геометрия там очень сложная и непонятно, какие там геометрические аксиомы. Дело в том, что бессердечная сука гравитация искривляет пространство. Прямыми логично называть траектории, по которым летают фотоны (сделаем вид, что это частица), а пространством — то, где они летают. Где и как, какая масса искривит пространство — вопрос сложный, поэтому пятый постулат там почти наверняка не выполняется. Куда интереснее другой вопрос. Если фотон полетит в одну сторону, то не вернётся ли он когда-нибудь «с другой стороны»? Если да, то это значит, что мы живём на сфере (правда, только трёхмерной) или на чём-то очень на это похожем. Ну или нет.

Видео:решение задач на параллельность прямыхСкачать

[править] Значимость

Работы Николая Иваныча, Бельтрами и прочих борцов за неевклидовость во многом перевернули математику как науку. Родились новые разделы математики, старые вышли на новый уровень. Вот несколько важных примеров.

[править] Аксиоматический метод

Уход от древнегреческого взгляда на аксиомы как на некие незыблемые б-гом данные сущности привёл к созданию математической логики и современной теории множеств. Выяснилось, что нужно не только доказывать новые теоремы в старой аксиоматике, но и сравнивать разные системы аксиом. Вообще оценивать их. К началу XX века из этого родятся работы Гильберта и Рассела, которые весьма романтически относились к аксиоматическому методу, считая, что он решит все проблемы в математике. Идеальным не может быть ничто, поэтому увенчалось это теоремами Гёделя, которые во многом определили границы применимости аксиоматического метода. Оные доставили немало баттхерта современникам и продолжают доставлять философам до сих пор. В добротной художественной форме об этом можно почитать в литературе.

[править] Геометрия

Старая добрая геометрия, в которой за 2 тысячи лет со времён самого Евклида мало что изменилось, вдруг вышла за пределы тех яслей, в которых сидела. От циркулей и линеек она наконец-то смогла перейти к изучению геометрии разных поверхностей, всяким необычным метрикам и всему тому, что так нужно и полезно в современной математике, физике и прочих естественных науках. Ведь и ты, анон, живёшь не на плоскости, а на сфере. А наша Земляшка крутится отнюдь не в обычном евклидовом трёхмерном пространстве. Да и вообще, многообразие Калаби-Яу и этим всё сказано.

[править] Per aspera ad astra

Ну и не только математика, конечно. Сам Лобачевский, хорошо понимая необходимость найти модель своей геометрии, пытался разглядеть эту модель в небе. Он считал расстояния и угол между звёздами, надеясь, что они будут описываться в терминах геометрии Лобачевского лучше, чем в евклидовой. Увы, но про релятивистские поправки и прочий необходимый матан тогда ещё известно не было. Но, как выяснится позже, он был не так уж и далёк от истины. Пространство Минковского как раз-таки близко к гиперболическому. И вообще, в современной астрофизике, в частности, при изучении чёрных дыр гиперболическая геометрия часто оказывается именно тем языком, на котором удобно решать многие задачи.

[править] Искусство

Ну и, конечно, сабж послужил источником вдохновения для многих художественных деятелей, начиная с писателей руками и кончая художниками. Немного спискоты, куда без неё.

• Эшер — во многих его произведениях используется тема замощений плоскости Лобачевского (в модели Клейна, например).
• Опрокинутый мир — годная книжка про то, каково жить в мире, который воспринимается как неевклидов.
• Песня из творчества Тома Лерера. Ознакомиться можно здесь.

Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

[править] Сабж сегодня

Сослужив службу высокой науке, геометрия Лобачевского нынче находится примерно в том же состоянии, что и евклидова геометрия, тригонометрия и прочие почтенные, заслуженные и полезные, но «закрытые» области математики.

При этом сабж находит применение как полигон для демонстрации разных математических теорем. В таком виде (и с этой целью) гиперболическая геометрия представлена в некоторых курсах этой вашей высшей математики. Сами по себе геометрические свойства в высокой науке™ всем уже похуй.

Впрочем, отдельные одаренные школьники для всяких юношеских научных конференций лабают разные теоремы в сабже, чаще всего являющиеся аналогами разных теорем из евклидовой геометрии. Эта деятельность является вполне годной как способ занять школиё полезным делом, но для современной фундаментальной науки эти результаты особого смысла не имеют. Но, опять же, если ты, мой юный друг, откроешь не баночку яги, а какое-нибудь новое свойство геометрии Лобачевского, это будет гораздо более полезно для твоего мозга.

Конечно, геометрия Лобачевского, как и любая не вполне очевидная теория, привлекает к себе внимание разных фриков, которые считают, что жидо математики дурят людям голову и скрывают истину. Другие обвиняют геометрию Лобачевского в бездуховности и осквернении наследия предков (древних греков). Особенно тут отличаются, к сожалению, фрики, которые считают себя носителями ГСМ. Впрочем, отсутствие естественно-научного склада мозга отнюдь не обозначает присутствие какого-либо мозга. Примеров фрик-шоу в интернетах вполне достаточно.

Видео:Коллеги думали, что у ученого "поехала крыша". Но он оказался УМНЕЕ | ГЕОМЕТРИЯ ЛОБАЧЕВСКОГОСкачать

[править] Небольшое послесловие

В принципе, геометрия Лобачевского вполне доступна для понимания даже рядового школьника. И вообще, идея отказаться от одной аксиомы в пользу другой не кажется такой уж сложной. Почему же джве тысячи лет отнюдь не глупые дяденьки так безнадёжно фейлили? Почему Николай Иваныч (а также Гаусс и Бойяи) такой молодец? Дело в том, что оказалось неимоверно сложным отнестись к аксиомам не как к заповедям, а как к вполне подвижной и изменчивой при необходимости штуке. Для тогдашних математиков заменить одну аксиому на другую было чем-то сродни замены одной заповеди на другую. Ты подумай, анон, что сделали бы с тем, кто предложил бы заменить «не укради» на «укради немедленно»?

Это сейчас мы понимаем, что математика сама по себе, а философия сама по себе, но в те времена это было смело, очень смело. Если сильно заинтересоваться вопросом, то окажется, что, например, церковникам от смелых опытов Лобачевского сильно припекло. И вообще, зачастую Николай Иваныча обвиняли не столько в формальных математических ошибках, сколько в бездуховности. Не зря гневные отзывы писали в весьма поцреотическом «Сыне отечества».

Вторая причина, на которой и стояла первая, была в том, что, начиная с Римской империи и особенно после темных веков средневековья, учёные, в том числе и математики, считали кошерным заниматься только (!) изучением наследия великих древнегреческих предков, альтернативой которому был мракобесный астрал. А значит, всё, чем они занимались, это развитием и расширением классических областей. Даже матан воспринимался и преподносился как развитие идей Архимеда, например. А за всякую самодеятельность современники могли на новатора весьма косо посмотреть. В XIX веке, конечно, было полиберальнее, но дух старой школы был ещё жив.

Была и третья причина, как Тарас Бульба и породившая, и убившая вторую. Математика до середины XIX века была наукой скорее описательной. Если есть задача, желательно восходящая к какому-нибудь Аристотелю с Пифагором, значит, есть смысл решать эту задачу и разрабатывать соответствующий научный аппарат. А отвечать на вопросы чисто математического содержания, появившиеся из других математических задач, считалось блажью, недостойной серьёзных людей. Это уже позже, к концу XIX века математика начнёт развиваться как самостоятельная наука в прямой связи с другими, «промышленными» задачами, и выяснится, что содержательные математические вопросы часто находят себе благодарных слушателей в практических областях, только вот почему-то никем не разработаны. Геометрия Лобачевского сыскалась в теории относительности, например. Так что достаточно условное разделение математической науки на фундаментальную и прикладную началось, в каком-то смысле, с работ Лобачевского.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

[править] Расстрельный математический список

Есть и такой. И многое в нём связано со смутными представлениями быдла о геометрии Лобачевского.

• Параллельные прямые пересекаются. Параллельные прямые не могут пересечься по определению. Хуита, которая пошла в массы из рекламы стиральных, сука, машин Zanussi. Из какого места высрался этот мем, науке неизвестно. Алсо, в геометрии Лобачевского некоторые (!) параллельные прямые пересекаются на абсолюте (то есть как бы в бесконечности), но в самой плоскости Лобачевского они не пересекаются. Потому что параллельные.

• Лобачевский опроверг геометрию Евклида. А Эйнштейн, видимо, отменил механику Ньютона. Тащемта, не опроверг, а продемонстрировал, что аксиоматика Евклида не единственная.

• Геометрия Лобачевского не имеет отношения к реальному миру. Бред, демонстрирующий тупость изрекающего. Модель геометрии Лобачевского ничем не хуже модели Евклида, и они обе применимы к соответствующим задачам. Идеальных евклидовых прямых и плоскостей в природе тоже как бы не существует, но в терминах что одной, что другой модели удобно работать во многих вполне прикладных задачах.

• Евклидова геометрия — это предельный случай геометрии Лобачевского. Формально фраза верная, но изрекающие не всегда понимают смысл оной. Технически имеется в виду следующее. Если в аналоге теоремы Пифагора для геометрии Лобачевского раскрыть гиперболические косинусы по формуле Тейлора, то первые слагаемые как бы дадут обычную теорему Пифагора. То есть при стремлении соответствующих величин к нулю формулы геометрии Лобачевского как бы превращаются (вырождаются) в формулы из геометрии Евклида. Отака хуйня, малята.

Однако подразумевают зачастую другой (бредовый) смысл. Если в модели Пуанкаре взять о-о-очень маленький кусок «плоскости» и там посмотреть на прямые, параллельные данной, проходящие через данную точку, то они будут все очень друг на друга похожи. А значит, если взять бесконечно малый кусок плоскости, то вроде как треугольники и прямые будут неотличимы от своих евклидовых аналогов.

📸 Видео

2. Пятый постулат геометрииСкачать

ГАЛИЯ ШАРАФЕТДИНОВА!!!!! 42 из 42 НА МЕЖНАРЕ-2022!! РАЗБОР ЗАДАЧ МЕЖНАРА С АБСОЛЮТНОЙ ЧЕМПИОНКОЙ!Скачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

#177. ГЕОМЕТРИЯ ЛОБАЧЕВСКОГО (советский диафильм)Скачать

#223. МИФЫ И ЛЕГЕНДЫ школьной математикиСкачать

7 класс, 28 урок, Аксиома параллельных прямыхСкачать