Доказать свойство медиан треугольника билет

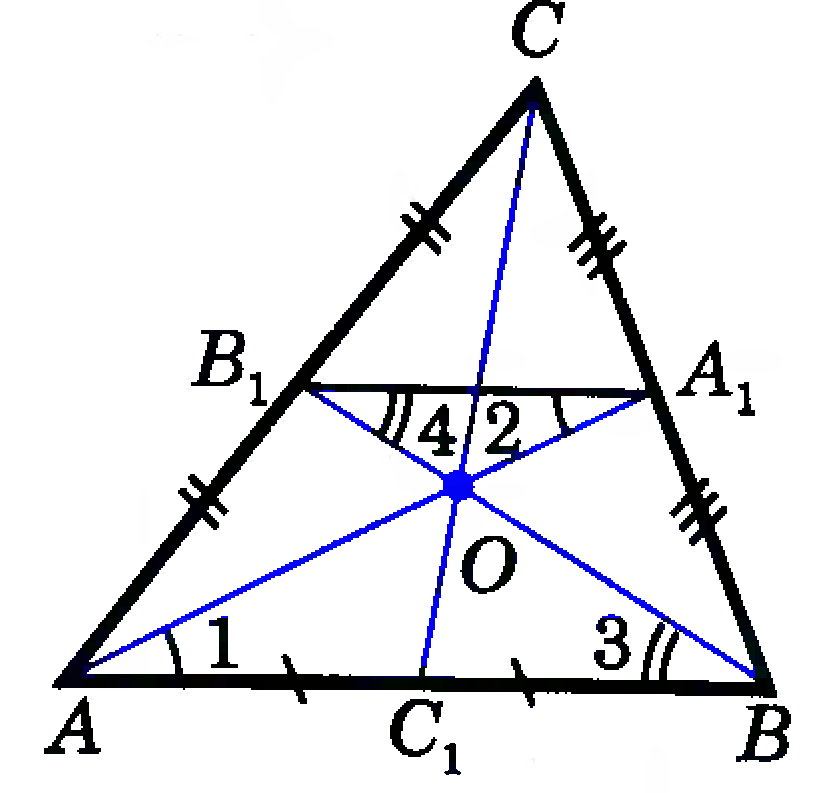
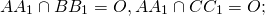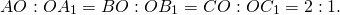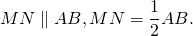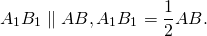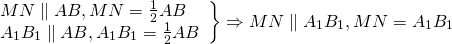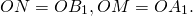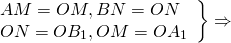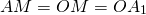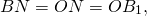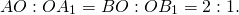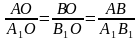Свойство медиан треугольника может быть доказано многими способами. Доказательство, опирающееся на свойства параллелограмма и средней линии треугольника, может быть проведено сразу же после изучения соответствующих тем, что позволяет начать использовать свойство медиан треугольника уже с начала 8 класса.

(Свойство медиан треугольника)

Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.

Дано : ABC, AA1, BB1, CC1 — медианы

1) Пусть M — середина отрезка AO, N — середина BO

(то есть AM=OM, BN=ON).

2) Соединим точки M, N, A1 и B1 отрезками.

3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.

Следовательно, A1B1 — средняя линия треугольника ABC и

Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).

По свойству диагоналей параллелограмма

из чего следует, что

5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.

Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.

Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.

Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:

Что и требовалось доказать .

Видео:8. Медиана треугольника и её свойства.Скачать

7 Comments

Промогите пожалуйста:
В прямоугольном треугольнике из вершины прямого угла до гипотенузы провели медиану длинной 50см и перпендикуляр 48см. Вычислить периметр.

Медиана, проведённая к гипотенузе, равна её половине. Следовательно, гипотенуза 100 см. Пусть катеты равны x см и y см. По теореме Пифагора x²+y²=100². Площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне S=0,5∙100∙48 см², либо половине произведения катетов S=0,5∙x∙y. Отсюда xy=4800.
Решаем систему уравнений: x²+y²=100²; xy=4800. Решения (60;80) (80;60). То есть катеты 60 см и 80 см. Периметр P=60+80+100=240 см.
(Не обязательно доводить решение системы до конца. Достаточно найти x+y. Для этого к 1-му уравнению прибавим удвоенное 2-е, получим
x²+2xy+y²=19600; x+y=140).

Прошу помощи в решении задачи: на стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.

Во-первых, большое спасибо за решение, даже не ожидала ответа, но, по счастью, ошиблась! Но я к этому времени уже решила так:провела ВМ, которая в равностороннем треугольнике является также высотой.
Рассмотрим четырехугольник ОВМС: угол ВОС =углу ВМС=90 градусов (диагонали ромба взаимно перпендикулярны),отсюда, ВМ параллельна ОС, тогда угол МОС=20 градусам. Рассм. треугольник ОМС: угол МСО= 180-20-70=90 градусов, и одновременно= 60+x, т.о., угол х=30 градусам, и искомый острый угол ромба=60 градусам. Мы получили разные ответы, в чем может быть дело (окружности мы еще не проходили).

Наталия углы BOC и BMC не накрест лежащие и не внутренние односторонние, поэтому BM не параллельна OC. Но вариант решения без окружности возможен, добавила второй способ.

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Билет 1, 2 изученое

Просмотр содержимого документа
«Билет 1, 2 изученое»

1 вопрос: дайте определение многоугольника, вершины, стороны, диагонали и периметра многоугольника. Запишите формулу суммы углов выпуклого многоугольника.

Определение. Многоугольником называют фигуру, составленную из отрезков так, что:

смежные отрезки не лежат на одной прямой

несмежные не имеют общих точек

Вершинами называются точки: А, В, С, D, E, F.

Сторонами многоугольника называются отрезки: AB, BC, CD, DE, ЕF, FA.

Диагональю многоугольника называется отрезок, соединяющий две любые не соседние вершины.

Периметром многоугольника называется сумма длин всех сторон.

Сумма углов выпуклого многоугольника равна (n-2) 180°

2 вопрос: докажите теорему о средней линни

4 вопрос: периметр прямоугольника равен 56, а диагональ равна 20. Найдите площадь этого прямоугольника.

1 вопрос: дайте определение и свойства параллелограмма.

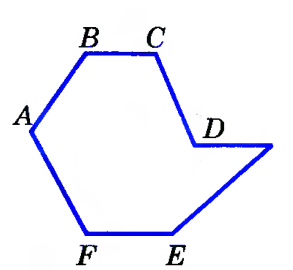
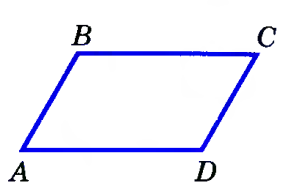
Определение. Параллелограмм – это четырехугольник, у которого противоположные стороны попарно – параллельны.

1° В параллелограмме противоположные углы равны. В параллелограмме противоположные стороны равны.

2° Диагонали параллелограмма точкой пересечения делится пополам.

3° В параллелограмме сумма углов прилежащих к одной стороне равна 180°.

4° Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

2 вопрос: доказать свойство медиан треугольника

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины

Дано: ∆АВС, О — точка пересечения медиан АА₁ и ВВ₁; А₁В₁ — средняя линия ∆АВС.

Доказать: точка О пересечение медиан АА₁ и ВВ₁ делит каждую из них в отношении 2:1, считая от вершины.

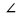
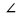
Отрезок А₁В₁ параллелен стороне АВ, поэтому 1 = 2 ; 3 = 4 (как накрест лежащие углы при пересечении параллельных прямых АВ и А₁В₁.).

Следовательно, треугольники АОВ и А₁ОВ₁ подобны по двум углам, и, значит, их стороны пропорциональны:

Но АВ=2 А₁В₁, поэтому АО=2 А₁О и ВО= 2 В₁О.

Таким образом, точка О пересечение медиан АА₁ и ВВ₁ делит каждую из них в отношении 2:1, считая от вершины.

Аналогично доказывается, что точка пересечения медиан ВВ₁ и СС₁ делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О.

Итак, все три медианы треугольника АВС пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.

Видео:🔥 Свойства МЕДИАНЫ #shortsСкачать

Материалы для подготовки к зачету по геометрии 8 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Материалы для подготовки к региональному зачету по геометрии для обучающихся 8 классов

Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Билет № 1

1)Определение многоугольника. Вершины, стороны, диагонали и периметр многоугольника. Формула суммы углов выпуклого многоугольника 2)Доказать теорему о средней линии треугольника.

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Билет №2

1)Определение и свойства параллелограмма.

2)Доказать свойство медиан треугольника

Видео:Теорема о трёх медианахСкачать

Билет №3

1) Определение и свойства прямоугольника 2) Доказать теорему Пифагора.

Видео:№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Билет №4

1) Определение и свойства ромба

2) Доказать теорему о вписанном угле (любой частный случай)

Видео:ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Билет №5

1) Определение трапеции. Виды трапеций.

2) Доказать свойство отрезков касательных, проведенных к окружности из одной точки.

Видео:Теорема о свойстве медианы равнобедренного треугольникаСкачать

Билет №6

1) Определение подобных треугольников. Признаки подобия треугольников 2) Доказать признак параллелограмма (по точке пересечения диагоналей). Билет №7

1) Синус, косинус и тангенс острого угла прямоугольного треугольника.

2) Доказать свойство диагоналей параллелограмма.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Билет №8

1) Значение синуса, косинуса и тангенса углов 30,45,60.

2) Доказать свойства противоположных сторон и углов параллелограмма.

Видео:Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

Билет №9

1)Определение секущей и касательной к окружности.

2)Доказать свойство диагоналей прямоугольника.

Видео:Длина медианы треугольникаСкачать

Билет №10

1) Определение вписанного и центрального углов окружности.

2) Доказать признак параллелограмма через равенство и параллельность двух противоположных сторон.

Видео:Урок 33. Свойство медиан треугольника (8 класс)Скачать

Билет №11

1)Определение серединного перпендикуляра к отрезку. Свойство серединного перпендикуляра.

2)Вывод формулы площади треугольника. Следствия. Формула Герона (без доказательства).

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Билет №12

1)Определение окружности, вписанной в многоугольник. Многоугольник, описанный около окружности.

Свойство описанного четырехугольника.

2)Доказать свойства диагоналей ромба.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Билет №13

1)Определение окружности, описанной около многоугольника. Многоугольник, вписанный в окружность. Свойства четырехугольника, вписанного в окружность.

2) Доказать свойство биссектрисы угла.

Видео:№366. Докажите, что если М — точка пересечения медиан треугольника ABC, а О — произвольная точкаСкачать

Билет №14

1)Окружность вписанная в треугольник. Окружность описанная около треугольника. Нахождение центров этих окружностей.

2) Свойство углов при основании равнобедренной трапеции.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Билет №15

2) Свойство отрезков пересекающихся хорд.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Билет 1

Вопрос 1: Определение многоугольника. Вершины, стороны, диагонали и периметр многоугольника. Формула суммы углов выпуклого многоугольника

Многоугольник – это геометрическая фигура, у которой смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.

Многоугольник с n вершинами называется n-угольником; он имеет n сторон. Примером многоугольника является треугольник (n=3), четырехугольник (n=4), шестиугольник (n=6), и. т. д.

Вершина многоугольника – это точка пересечения двух соседних сторон многоугольника.

Сторона многоугольника – это отрезок соединяющий две соседние вершины многоугольника.

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника ABCDE равен: Р=AB + BC+ CD + DE + EA

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ многоугольника – это отрезок, соединяющий две любые не соседние вершины многоугольника. Например, отрезок AD является диагональю:

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Сумма углов выпуклого n-угольника равна (n-2)∙ 180 .̊

Сумма углов выпуклого четырехугольника равна 360 .̊

Вопрос 2: Доказать теорему о средней линии треугольника.

Средняя линия треугольника это отрезок соединяющий середины двух сторон треугольника.

В треугольнике можно провести три средних линии.

Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

1. МN- средняя линия треугольника АВС  BM=MA, BN=NC.

2. Рассмотрим треугольники BMN и BAC.

Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Отсюда следует, что

По признаку параллельности прямых MN||AC.

2. Также из подобия треугольников следует, что

 MN= AC

Что и требовалось доказать.

Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Билет №2

Вопрос 1: Определение и свойства параллелограмма.

Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.

1. В параллелограмме противоположные стороны равны и противоположные углы равны.

2. Диагонали параллелограмма пересекаются и точкой пересечения делятся

Вопрос 2: Доказать свойство медиан треугольника.

Свойство медиан треугольника: Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины. Дано:  АВС

AM, BD и CN – медианы,

Доказать, что: СР=2РN, АР=2МР, ВР=2РD/

Пусть в треугольнике АВС AM, BD и CN – медианы,

Р – точка их пересечения. Тогда МN – средняя линия треугольника АВС, поэтому MN параллельна стороне АС и равна ее половине. Треугольники АСР и MNP подобны (по двум углам)

можно доказать, что . Так как попарно точкой пересечения медианы

делятся в одном и том же отношении, то они пересекаются в одной точке.

Что и требовалось доказать.

Вопрос 1: Определение и свойства прямоугольника.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма.

1. Противоположные стороны прямоугольника равны: AB=CD, BC=AD.

2. Каждый угол прямоугольника равен 90°.

Это значит, что противоположные углы равны и сумма углов, прилежащих к одной стороне, равна 180°.

3. Диагонали прямоугольника точкой пересечения делятся пополам: BO=OD, AO=OC.

4. Диагонали прямоугольника равны: BD=AC.

А также BO=OD=AO=OC

Вопрос 2: Доказать теорему Пифагора.

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: с 2  а 2  b 2 .

Дано: треугольник АВС- прямоугольный, АВ = с, ВС= b, АС = а, угол С =90°.

Доказать: с 2 = а 2 + b 2 .

а) Построим прямоугольный треугольник АВС;

б) Достроим треугольник АВС до квадрата СKPD со стороной (а+b );

S_CKPD = (a+b) 2 = a 2 + 2ab + b 2 .

в) Рассмотрим треугольники: BCА, AKE, EPM и MDB, они равны по двум катетам, а у равных фигур — равные площади, т.е.

S BCA = S AKE = S EPM = S MDB = ab/2.

г) ВАЕМ – квадрат, S_BAEM = с 2 .

д) S_CKPD = S_BCA + S_AKE + S_EPM + S_MDB+ S_BAEM = 4•ab/2 + с 2 = 2ab + с 2 . а 2 + 2ab + b 2 = 2ab + с 2 ; с 2 = а 2 + b 2 .

Что и требовалось доказать.

Вопрос 1: Определение и свойства ромба.

Ромбом называется параллелограмм, у которого все стороны равны.

Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма

1. Противоположные стороны ромба равны: AB=BC=CD=AD (т. к. все стороны равны).

2. Противоположные углы ромба равны: p А  p С , p В  p D .

3. Диагонали ромба точкой пересечения делятся пополам: BO=OD; AO=OC.

4. Диагонали ромба взаимно перпендикулярны: AC BD.

5. Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).

Вопрос 2: Доказать теорему о вписанном угле (любой частный случай).

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается:

p ACB   AB .

При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.

Первый случай. Сторона вписанного угла проходит через центр окружности.

Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, A = B, как углы при основании равнобедренного треугольника.

Так как AOC – внешний угол равнобедренного треугольника, то: AOC = A + B,

а так как углы A и B равны, то  В   _АОС . Но AOC – центральный угол, значит AOC = AC, следовательно B измеряется половиной дуги AC:

ABC AC

Второй случай. Центр окружности лежит между сторонами вписанного угла.

Проведём диаметр BD. Угол ABC разбился на два угла: 1 и 2.

Точка D разделяет дугу AC на две дуги: AD и DC. По доказательству, рассмотренному в первом случае:

1 = AD и 2 = DC

Следовательно, весь угол ABC будет измеряться половиной дуги AC:

1 + 2 = AD + DC

ABC = AC.

Третий случай. Центр окружности лежит вне вписанного угла.

Проведём диаметр BD.

ABC = ABD — CBD. Но ABD измеряется половиной дуги AD , а CBD измеряется половиной дуги CD. Следовательно,  АВС  (  АD   СD ), то есть  ABC  AC .

Что и требовалось доказать.

Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Следствие 2. Вписанный угол, опирающийся на полуокружность- прямой.

Видео:Все свойства медианы в одной задаче.Скачать

Билет 5

Вопрос 1. Определение трапеции. Виды трапеций.

Трапеция — это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.

AD, ВС — основания; AB, CD — боковые стороны.

1. Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.

Также встречаются такие названия, как равнобокая или равнобочная.

2. Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.

Вопрос 2. Доказать свойство отрезков касательных, проведенных к окружности из одной точки.

Теорема: Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

АВ=АС, BAO= CAO

Дано: окружность (O;R),

АВ и АС- касательные к окружности (O;R),

В,С- точки касания

Доказать, что AB=AC, BAO=CAO.

(как радиусы, проведенные в точку касания ) .

Следовательно, треугольники ABO и ACO — прямоугольные. У них

1) катеты OB=OC (как радиусы)

2) гипотенуза OA — общая сторона.

Из равенства треугольников следует равенство соответствующих сторон:

AB=AC и соответствующих углов: ∠ BAO= ∠ CAO.

Что и требовалось доказать.

Билет №6

Вопрос 1. Определение подобных треугольников. Признаки подобия треугольников.

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Даны треугольники ABC и DEF.

АВ BC AC , p A  p D , p B  p E , p C  p F , то можно

Если известно, что    k

сделать вывод, что ΔABC ∼ ΔDEF .

Число k, которое равно отношению соответствующих сторон треугольников, называется коэффициентом подобия треугольников.

Первый признак подобия треугольников

Теорема: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

p А  p А ₁ , p С  p С ₁  АВС _{ А 1} B ₁ C ₁ .

Второй признак подобия треугольников

Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

 , p A  p A ₁

Третий признак подобия треугольников

Теорема: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

 

Вопрос 2: Доказать признак параллелограмма (по точке пересечения диагоналей).

ТЕОРЕМА (III признак параллелограмма). Если в четырехугольнике диагонали

пересекаются и точкой пересечения делятся пополам, то этот четырехугольник-

Дано: ABCD – четырёхугольник,

AC и BD – диагонали,

Доказать: ABCD – параллелограмм.

Рассмотрим ∆AOB и ∆COD .

AO = OC (по условию)

BO = OD (по условию) | ⟹ ∆AOB = ∆COD по I признаку

∠AOB = ∠COD (как вертикальные) равенства треугольников ⟹ AB = CD и ∠ABO = ∠CDO . А эти углы являются внутренними накрест лежащими при прямых AB и CD , значит, AB ∥ CD .

Мы доказали, что в четырёхугольнике ABCD две стороны параллельны и равны ( AB = CD, AB ∥ CD ), значит, по I признаку, этот четырёхугольник является параллелограммом,

Что и требовалось доказать.

Билет №7

Вопрос 1: Синус, косинус и тангенс острого угла прямоугольного треугольника.

В прямоугольном треугольнике тригонометрические функции используются для вычисления сторон и острых углов треугольника.

а и b- катеты, c- гипотенуза.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе.

.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.

.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к прилежащему катету.

.

Вопрос 2: Доказать свойство диагоналей параллелограмма.

Теорема: Диагонали параллелограмма точкой пересечения делятся пополам.

Дано: ABCD – параллелограмм

AC и BD – диагонали

Доказать: BO = OD, AO = OC.

1. Рассмотрим ∆AOD и ∆COB .

AD = BC (по свойству сторон параллелограмма)

∠OAD = ∠OCB (как внутренние накрест лежащие при ∥ прямых)| ⟹

∠ODA = ∠OBC (как внутренние накрест лежащие при ∥ прямых)

∆AOD = ∆COB по II признаку равенства треугольников ⟹ AO = OC, OD = BO .

Что и требовалось доказать.

Билет №8

Вопрос 1: Значение синуса, косинуса и тангенса углов 30 ° ,45 ° ,60 ° .

Таблица значений синуса, косинуса и тангенса углов 30 ° ,45 ° ,60 ° .

2

3

3

2

3

3

Вопрос 2: Доказать свойства противоположных сторон и углов параллелограмма.

Свойство параллелограмма: В параллелограмме противоположные стороны равны и противоположные углы равны.

ABCD – параллелограмм Доказать: AB = CD, BC = AD, ∠A = ∠C, ∠B = ∠D.

1. Проведём диагональ BD . Рассмотрим ∆ABD и ∆CDB .

∠ABD = ∠CDB (как внутренние накрест лежащие при ∥ прямых)| ⟹ ∠ADB = ∠CBD (как внутренние накрест лежащие при ∥ прямых)

⟹ ∆ABD = ∆CDB по II признаку равенства ∆ ⟹ AB = CD, BC = AD, ∠A =

2. ∠B и ∠A ; ∠D и ∠A – внутренние односторонние при параллельных прямых, значит,

.

3. Итак, AB = CD, BC = AD, ∠A = ∠C, ∠B = ∠D .

Что и требовалось доказать.

Билет №9

Вопрос 1: Определение секущей и касательной к окружности.

В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь одну или две общие точки.

1. Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет.

2. Если расстояние от центра окружности до прямой меньше радиуса, то у прямой и окружности две общие точки.

В этом случае прямую называют секущей окружности.

Если прямая имеет две общие точки с окружностью, то она называется секущей.

3. Если расстояние от центра окружности до прямой равно радиусу, то у прямой и окружности одна общая точка.

В этом случая прямую называют касательной к окружности.

Касательной к окружности называется прямая, имеющая с окружностью одну общую точку .

Теорема : Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Вопрос 2: Доказать свойство диагоналей прямоугольника.

Свойство прямоугольника: Диагонали прямоугольника равны.

Дано: ABCD — прямоугольник, AC и BD — диагонали.

Рассмотрим прямоугольные треугольники ABD и DCA.

BAD=CDA=90º (по определению прямоугольника).

1) Катеты AB=DC (как противолежащие стороны прямоугольника).

2) Катет AD — общий.

Следовательно, треугольники ABD и DCA равны (по двум катетам ) .

Из равенства треугольников следует равенство соответствующих сторон: AC=BD.

Что и требовалось доказать.

Билет №10

Вопрос 1: Определение вписанного и центрального углов окружности.

Центральный угол — это угол с вершиной в центре окружности.

∠ AOВ — центральный. точка O – вершина, центр окружности. лучи OA и OВ- стороны, пересекают окружность.

Градусная мера центрального угла равна градусной мере соответствующей дуги окружности: ∠ AOВ = ∪ AB.

Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ AСВ – вписанный.

Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается:

∠ AСВ=  АВ .

Вопрос 1: Доказать признак параллелограмма через равенство и параллельность двух противоположных сторон.

ТЕОРЕМА (I признак параллелограмма). Если в четырёхугольнике две стороны равны и параллельны, то такой четырёхугольник является параллелограммом.

Дано: ABCD – четырёхугольник BC ∥ AD, BC = AD

Доказать: ABCD – параллелограмм.

Проведём диагональ BD и рассмотрим ∆ABD и ∆CDB .

⟹ ∆ABD = ∆CDB по I признаку равенства треугольников ⟹

⟹ ∠ABD = ∠CDB (по определению равных треугольников) . Эти углы являются внутренними накрест лежащими при прямых AB и CD , значит, по признаку параллельности прямых, AB ∥ CD .

Итак, в четырёхугольнике ABCD AB ∥ CD, BC ∥ AD , т.е. стороны попарно параллельны, значит, ABCD – параллелограмм (по определению).

Что и требовалось доказать.

Билет №11

Вопрос 1: Определение серединного перпендикуляра к отрезку. Свойство серединного перпендикуляра.

— серединный перпендикуляр к отрезку АВ.

Теорема: Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.

m — серединный перпендикуляр отрезка АВ, О — середина АВ, АМ=МВ.

Следствие: Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Вопрос 2: Вывод формулы площади треугольника. Следствия. Формула Герона (без доказательства).

Одну из сторон треугольника часто называют его основанием . Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведённую к основанию.

Теорема: Площадь треугольника равна половине произведения его

основания на высоту:

АВ-основание СН- высота.

Доказать, что

1.Достроим треугольник АВС до параллелограмма ABDC так, как показано на рисунке.

2. Рассмотрим  АВС и  DCB

АВ = CD и АС = BD как противоположные стороны параллелограмма ABDC

Следовательно,  АВС =  DCB ( по III признаку)  S _{ABC } 1 S _ABCD

 S _{ ABC}  AB  CH .

Что и требовалось доказать.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов.

S  а  b .

Следствие 2. Если высоты двух треугольников равны, то и площади относятся как основания.

Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.

Формула Герона: где – полупериметр:

Билет №12

Вопрос 1: Определение окружности, вписанной в многоугольник. Многоугольник, описанный около окружности. Свойство описанного четырехугольника.

Окружность вписанная в многоугольник — это окружность , которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана.

Описанный около окружности многоугольник — это многоугольник, в который вписана окружность. На рисунке

1 четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

Замечание 1: В треугольник можно вписать только одну окружность .

Замечание 2: Не во всякий четырехугольник можно вписать окружность .

Замечательное свойство: В любом описанном четырехугольнике суммы противоположных сторон равны: a + c= b + d.

Верно и обратное утверждение: Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность .

Вопрос 2: Доказать свойства диагоналей ромба.

Свойство ромба: Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Дано: ABCD – ромб

AC и BD диагонали.

Доказать: AC ⊥ BD , p BAC  p DAC

1.По определению ромба АВ=АD  BAD  равнобедренный.

2. Так как ромб – параллелограмм, то его диагонали точкой O пересечения делятся пополам  АО-медиана  BAD , а значит высота и биссектриса этого треугольника. Поэтому AC ⊥ BD и p BAC  p DAC .

Что и требовалось доказать.

Билет 13

Вопрос 1: Определение окружности, описанной около многоугольника. Многоугольник, вписанный в окружность. Свойства четырехугольника, вписанного в окружность.

Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности.

На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема: Около любого треугольника можно описать окружность .

Замечание 1: Около треугольника можно описать только одну окружность .

Замечание 2: Около четырехугольника не всегда можно описать окружность .

Замечательное свойство: В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 : p ABC  p ADC .

Верно и обратное утверждение: Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность .

Вопрос 2: Доказать свойство биссектрисы угла.

Свойство биссектрисы угла: Каждая точка биссектрисы неразвернутого угла равноудалена от сторон этого угла.

Обратно : каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Дано: BD — биссектриса ∠ ABC, F ∈ BD,

Рассмотрим треугольники BFK и BFP.

∠ BKF= ∠ BPF=90º, ∠ KBF= ∠ PBF (так как по условию BD — биссектриса ∠ ABC).

BF — общая сторона.

Что и требовалось доказать.

Обратно : каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Треугольники BFK и BFP в этом случае равны по катету и гипотенузе (FK=FP по условию, BF — общая сторона). Из равенства треугольников следует равенство соответствующих углов: ∠ KBF= ∠ PBF, а значит, BD — биссектриса ∠ ABC.

Что и требовалось доказать.

Билет №14

Вопрос 1: Окружность вписанная в треугольник. Окружность описанная около треугольника. Нахождение центров этих окружностей.

Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности.

Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника. Следовательно, около любого треугольника можно описать окружность, так как серединные перпендикуляры к сторонам пересекаются в одной точке.

Для остроугольного треугольника центр окружности находится в треугольнике.

Другая ситуация с прямоугольным и тупоугольным треугольниками.

Окружность называют вписанной в треугольник, если все стороны треугольника касаются окружности.

Её центр равноудалён от всех сторон, то есть должен находиться в точке пересечения биссектрис треугольника.

Следовательно, в любой треугольник можно вписать окружность, так как биссектрисы треугольника пересекаются в одной точке.

Так как биссектрисы углов треугольника всегда пересекаются внутри треугольника, то для всех треугольников центр вписанной окружности находится в треугольниках.

Вопрос 2: Свойство углов при основании равнобедренной трапеции.

Свойство равнобедренной трапеции: Углы при основании равнобедренной трапеции равны.

Дано: ABCD — трапеция,

Доказать: ∠ A= ∠ D, ∠ B= ∠ C.

1) Проведем из вершин тупых углов высоты BМ и CN:

2) Рассмотрим треугольники ABM и CND.

∠ AMB=90º, ∠ CND=90º (так как BM и CN— высоты трапеции).

AB=CD (по условию),

BM=CN (как высоты трапеции).

Отсюда следует, что треугольники ABM и CND равны ( по катету и гипотенузе )  ∠ A= ∠ D.

3) ∠ A+ ∠ ABC=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Отсюда, ∠ ABC=180º- ∠ A.

Аналогично, ∠ D+ ∠ DCB — внутренние односторонние при AD ∥ BC и секущей CD, и ∠ DCB=180º- ∠ D.

Так как ∠ A= ∠ D, то и ∠ ABC= ∠ DCB.

Что и требовалось доказать.

Билет №15

Вопрос 1: Теорема Фалеса.

Теорема Фалеса: Если параллельные прямые, пересекающие стороны угла, отсекают на одной из его сторон равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Теорему Фалеса используют, чтобы разделить отрезок на несколько равных частей.

Необходимо разделить отрезок AB на 7 равных частей.

Нарисуем угол, на одной стороне которого лежит отрезок AB. Сторону угла BC нарисуем по клеточкам и используем клеточки для деления стороны на 7 равных частей:

BD=DE=EF=FG=GH=HJ=JC. Концы обоих отрезков соединяем, получаем AC.

Проводим прямые, параллельные AC, начинающиеся в точках J,H,G,F,E,D, получаем 7 параллельных прямых (опять используем клеточки).

Если BD=DE=EF=FG=GH=HJ=JC и ACJKHLGMFNEPDR, то по теореме Фалеса BR=RP=PN=NM=ML=LK=KA.

Вопрос 2: Свойство отрезков пересекающихся хорд.

Теорема: Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды:

.

Докажем, что

Рассмотрим треугольники AOC и DOB.

(вертикальные)

(как опирающиеся на дугу BC).

(по двум углам).

Отсюда .