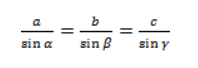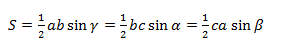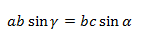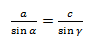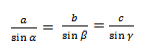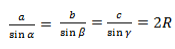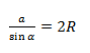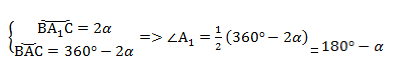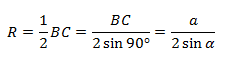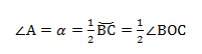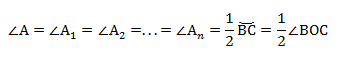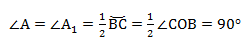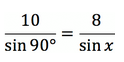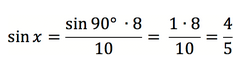Треугольник авс вписан в окружность угол а равен 60

Видео:Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

Треугольник вписанный в окружность

Видео:Геометрия В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касаетсяСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = frac ab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Треугольник ABC вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Геометрия ОГЭ задача Теорема синусовСкачать

В треугольнике ABC ∠A = 60°. Радиус окружности, вписанной в этот треугольник, равен 1 см. Найдите расстояние от точки касания окружности

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Ваш ответ

Видео:В треугольнике ABC углы A и C равны 20° и 60° ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

решение вопроса

Видео:В треугольнике АВС углы А и С равны 40 и 60 градусовСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,006
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№223. Найдите угол С треугольника ABC, если: a) ∠A=65°, ∠B = 57°; б) ∠A = 24°, ∠B= 130Скачать

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

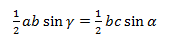
На b сокращаем, синусы переносим в знаменатели:

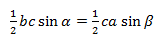
bc sinα = ca sinβ

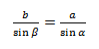
Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Видео:ОГЭ. Геометрия. 1 часть. Теорема синусов.Скачать

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

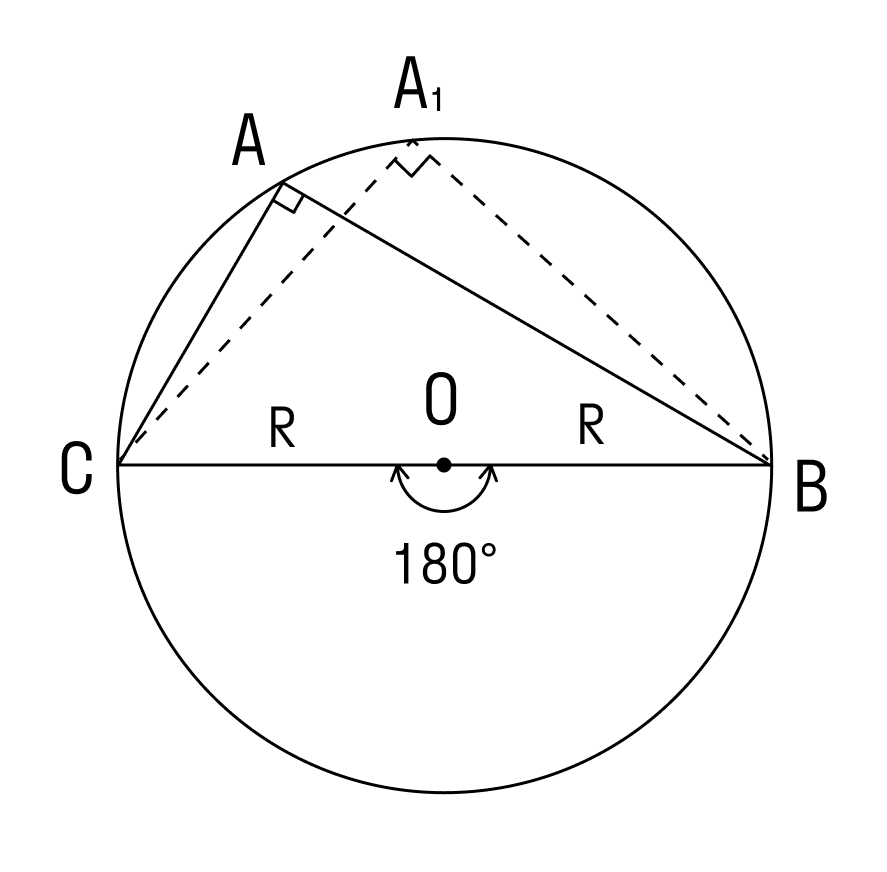
3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

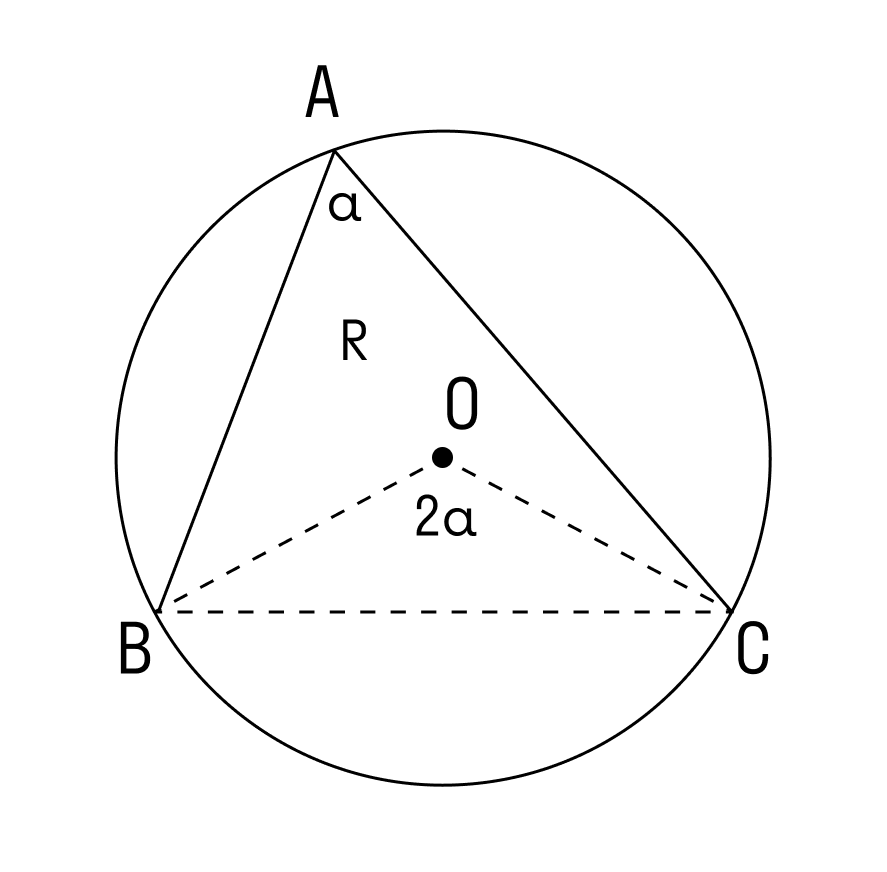
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

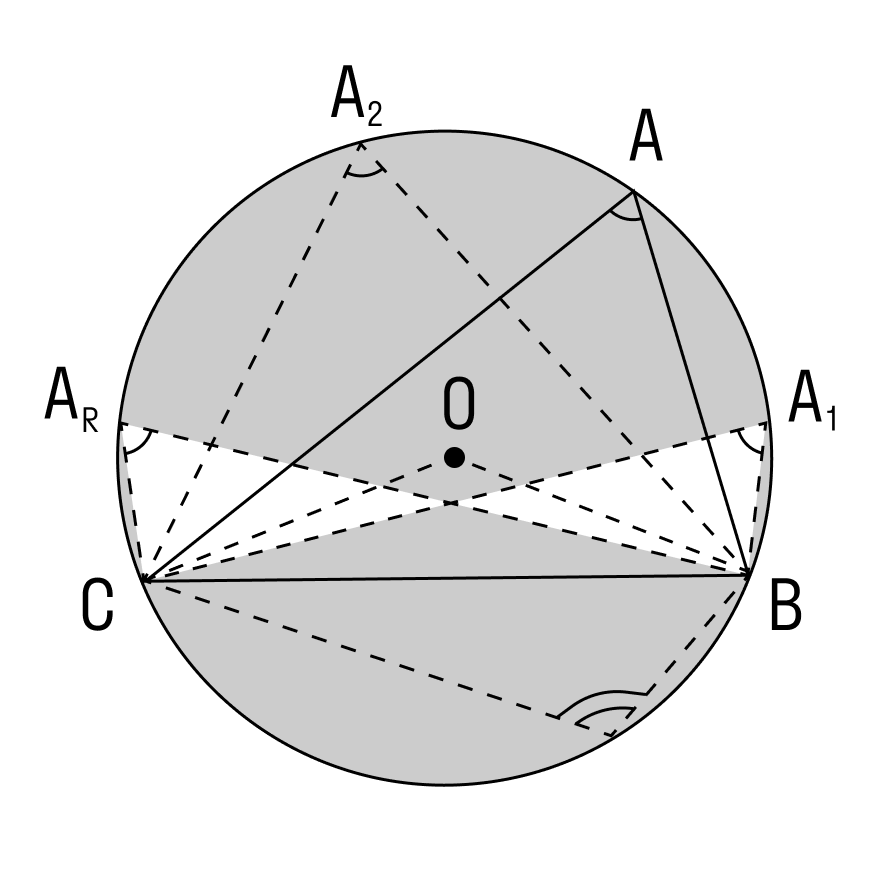
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Видео:Диагностическая работа-1 в формате ОГЭ. Задача-25Скачать

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

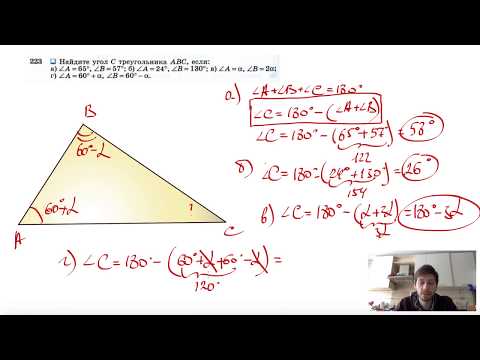
Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

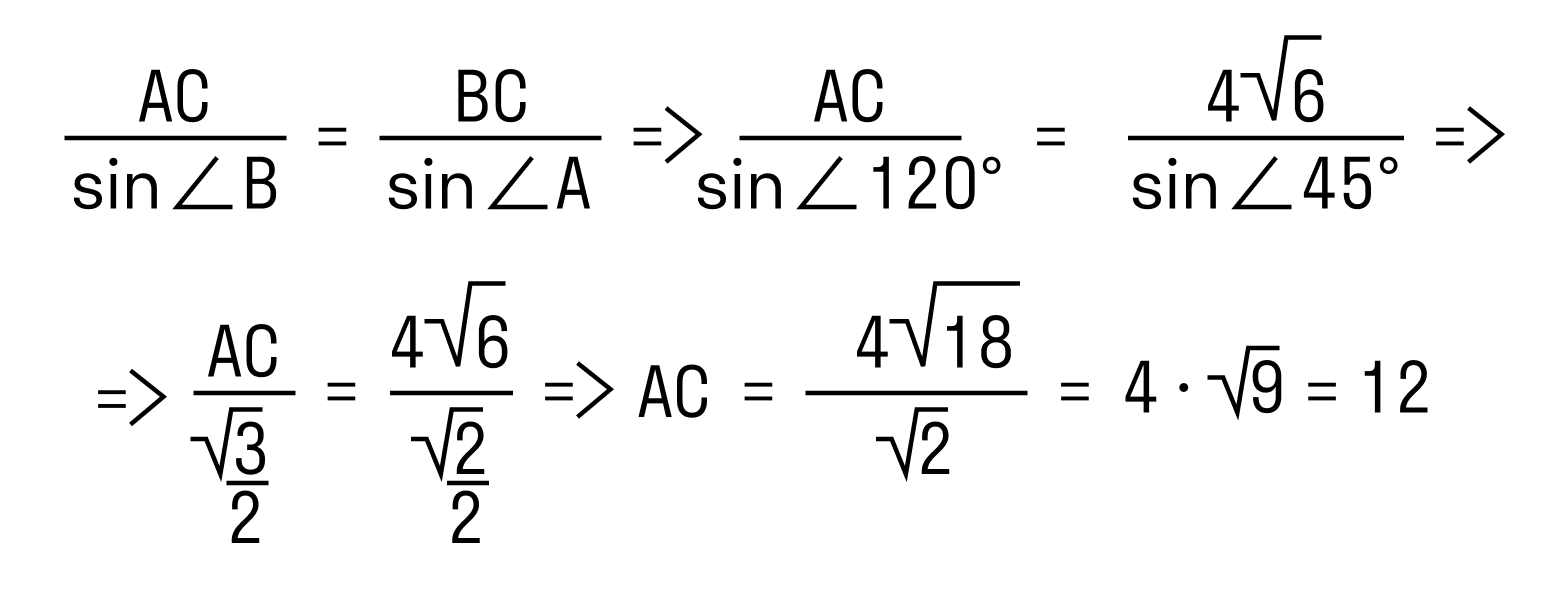
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Видео:№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

В треугольнике ABC ∠A = 60°. Радиус окружности, вписанной в этот треугольник, равен 1 см. Найдите расстояние от точки касания окружности

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Ваш ответ

Видео:№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

решение вопроса

Видео:ОГЭ математика +21,22,24 #8.18 Задача 17🔴Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,044
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Построить угол 60°Скачать

Треугольник АВС вписан в окружность, угол АВС равен 60 градусов?

Геометрия | 10 — 11 классы

Треугольник АВС вписан в окружность, угол АВС равен 60 градусов.

Найдите величину дуги АВ, если дуга АВ равна двум дугам ВС.

Обозначит дугу АВ за 2х, а ВС за х

К. угол В вписанный дуга АС = 120

2х + х + 120 = 360

дуга АВ = 80 * 2 = 160.

ПОМОГИИИТЕЕ?

В окружность вписан треугольник АВС так, что сторона АС является диаметром этой окружности.

Найдите углы треугольника АВС, если дуга ВС = 108 градусов.

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2?

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2.

Найди углы треугольника ОАВ.

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2?

Вершины треугольника АВС лежат на окружности с центром О, угол АВС = 80 грудусов, дуга ВС : на дугу АВ = 3 : 2.

Найди углы треугольника ОАВ.

Угол АКВ вписан в окружность и равен 45 градусов?

Угол АКВ вписан в окружность и равен 45 градусов.

Найдите дугу АВ, если R = 4.

Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно?

Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно.

Найдите дугу MK, дугу MN, дугу NK, если угол АВС = 62 градусам, угол АСВ = 68 градусам.

Точки А, В, С лежат на окружности с центром О?

Точки А, В, С лежат на окружности с центром О.

Угол АОВ = 80 градусов, дуга АС : на дугу ВС — 2 : 3.

Найдите углы треугольника АВС.

В окружность вписан треугольник АВС так, что АВ — диаметр окружности?

В окружность вписан треугольник АВС так, что АВ — диаметр окружности.

Найдите углы треугольника, если дуга АС = 70 градусов (Помогите пжл : * ).

Треугольник АВС, у которого АС = 6, угол А = 75 градусов , угол В = 30 градусов, вписан в окружность?

Треугольник АВС, у которого АС = 6, угол А = 75 градусов , угол В = 30 градусов, вписан в окружность.

Найдите длины дуг окружности, концами которых являются вершины треугольника.

Точки А, В, С лежат на окружности с центром О, угол АОВ равен 80 градусов, дуга АВ относится к дуге ВС, как 2 относится к 3, Найдите углы треугольника АВС?

Точки А, В, С лежат на окружности с центром О, угол АОВ равен 80 градусов, дуга АВ относится к дуге ВС, как 2 относится к 3, Найдите углы треугольника АВС.

В окружность вписан треугольник АВС так, что АВ – диаметр окружности?

В окружность вписан треугольник АВС так, что АВ – диаметр окружности.

Найдите углы треугольника, если дуга ВС = 134°.

Вы открыли страницу вопроса Треугольник АВС вписан в окружность, угол АВС равен 60 градусов?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Возможно, кому — то пригодится решение — привожу своё : Пусть BC = AD = aBC = AD = a, тогда из условия BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5. MOMO и ONON найдём как средние линии трапеций ..

Решение 22см — одна из сторон, т. К. сумма от точки пересекч к соседним сторонам равна одной стороне. 22 — 6 = 16см — вторая сторона.

Х + х — 6 = 22 2х — 6 = 22 2х = 22 + 6 2х = 28 х = 28 / 2 х = 14 одна сторона это Х то есть 14 а вторая х — 6 то есть 14 — 6 = 8.

1) вектор а = 2i — j 2) координаты вектора c .

Вот, пожалуйста✩ ^ _ ^ Все очень просто решается по теореме Пифагора.

Решение задания приложено.

ВС = MB — MC = 18, 2 — 9, 4 = 8, 8 Ответ : 1.

1). треугольники КВА = КАD по 2 — ум сторонам и углу между ними, т. К. АD = АВ (ABCD ромб), КА — общая, углы КАВ = КАD. 2) Из равенства треугольников следует что КВ = КD.

3 и 4 не могут существовать, т. К у треугольника сумма любых двух сторон должна быть больше третьей.

Примем коэффициент подобия стороны треугольника за — х, значит : ▪одна сторона — 4х ▪ вторая сторона — 6х ▪ третья сторона — 7х ▪периметр треугольника это сумма всех его сторон, а т. К. тругольники подобные, значит стороны одного треуг. Соответстве..