Сколько точек может оказаться в пересечении отрезка и окружности (5 видео)

Школе NET

Содержание

Register
Login
Newsletter
Главный Попко
Сколько точек может оказаться в пересечении 1)прямой и окружности 2)двух окружностей
Всё про окружность и круг
Пересечение Окружности Отрезка Линии
5 ответов
🎦 Видео

Register

Do you already have an account? Login

Don’t you have an account yet? Register

Submit to our newsletter to receive exclusive stories delivered to you inbox!

Главная 
Вопросы & Ответы 
Вопрос 5905369

Главный Попко

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сколько точек может оказаться в пересечении 1)прямой и окружности 2)двух окружностей

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Пересечение Окружности Отрезка Линии

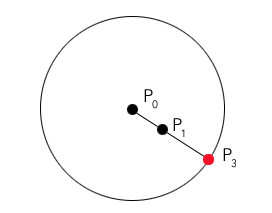
Я пытаюсь определить точку, в которой отрезок линии пересекаются окружности. Например, учитывая любую точку между P0 и P3 (а также предполагая, что вы знаете радиус), какой самый простой способ определить P3?

Видео:Определение точки пересечения окружности с прямойСкачать

5 ответов

у вас есть система уравнений. Круг определяется: x^2 + y^2 = r^2 . Линии определяется y = y0 + [(y1 — y0) / (x1 — x0)]·(x — x0) . Подставьте вторую в первую, вы получите x^2 + (y0 + [(y1 — y0) / (x1 — x0)]·(x — x0))^2 = r^2 . Решите это, и вы получите значения 0-2 для x. Подключите их обратно в любое уравнение, чтобы получить ваши значения для y.

найти угол между P0 и P1
нарисуйте линию под этим углом от P0 на расстоянии r, что даст вам P3

из центра круга и радиуса вы можете написать уравнение, описывающее круг. Из двух точек P0 и P1 можно написать уравнение, описывающее линию.

таким образом, у вас есть 2 уравнения в 2 неизвестных, которые вы можете решить путем замены.

и (x1,y1) = координаты точки P1

уравнение для круга:

уравнение для строка:

подключение 2-го уравнения в первое, получим:

аналогично вы можете найти, что

точка (x,y) — это точка пересечения между линией и кругом, (x,y) — ваш ответ.

перейти к этому коду..его сэкономить время

КОД MATLAB

функция [ флаг] = circleLineSegmentIntersection2 (Ax, Ay, Bx, By, Cx, Cy, R)

% A и B — две конечные точки отрезка линии, а C-центр окружность, % R-радиус окружности. Эта вычислительная функция ближайшая точка fron C к сегменту %, если расстояние до ближайшая точка > R возврат 0 else 1