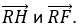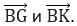Тренажер угол между векторами (6 видео) | Курс школьной геометрии

Тренажер угол между векторами

Тесты по геометрии 9 класс. Тема: «Угол между векторами. Скалярное произведение векторов»

Правильный вариант ответа отмечен знаком +

1. Дайте определение понятию «вектор»:

— отрезок, соединяющий две точки, расположенные в разных четвертях векторной плоскости

— прямая, проходящая через три равноудаленные точки

+ направленный отрезок, для которого указано, какая из точек является началом, а какая концом

— любая скалярная величина, выраженная положительным числом

2. Два вектора, которые … либо лежат на одной прямой, называются коллинеарными. Вставьте пропущенную фразу.

— перпендикулярны друг другу

— выходят из одной точки

— равны друг другу

+ параллельны одной прямой

3. Как называются векторы, которые являются противоположными противоположно направленным векторам?

— направленные в одну сторону

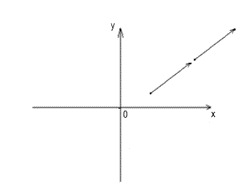
4. Какими являются векторы, изображенные на рисунке:

+ коллинеарными и сонаправленными

— коллинеарными и противоположно направленными

— неколлинеарными и равными

— равными и противоположно направленными

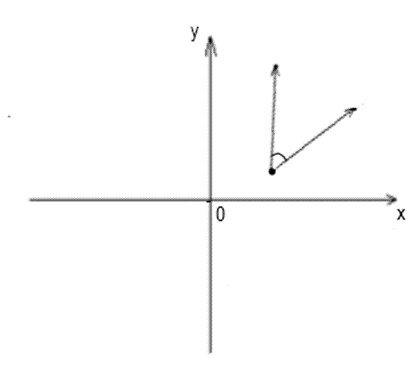
5. Кратчайший угол, на который нужно повернуть один вектор вокруг своего начала до положения сонаправленности с другим вектором называется:

-углом между векторами, выходящими из разных точек

+ углом между векторами, выходящими из одной точки

— углом между коллинеарными векторами

— углом между противоположно направленными векторами

6. Если угол между векторами равен 0 o , следовательно, векторы:

— выходят из начала координат

7. Угол между противоположно направленными векторами равен:

8. Как называются векторы, угол между которыми прямой?

9. Дан ромб RHKF. Известно, что RH=RK. Найдите угол между векторами

тест 10. Как иначе называется длина вектора?

11. Как вычислить длину вектора, если известны его координаты?

+ она равна квадратному корню из суммы квадратов координат

— она равна произведению квадратов координат

— она равна отношению произведения координат к сумме их квадратов

— она равна сумме квадратов координат

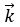
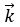
12. Известно, что координаты вектора равны . Найдите модуль вектора .

13. Что такое скалярное произведение двух векторов?

— произведение координат векторов

— произведение квадратов длин этих векторов

— произведение квадратов модулей этих векторов на синус угла между ними

+ произведение модулей этих векторов на косинус угла между ними

14. В каком случае скалярное произведение ненулевых векторов равно нулю?

— если они коллинеарны

+ если они перпендикулярны друг другу

— если они сонаправлены

— если они противоположно направлены

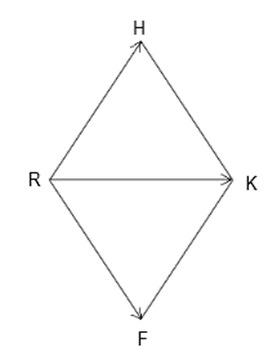
15. Скалярное произведение векторов, изображенных на рисунке, будет:

16. Может ли скалярное произведение векторов быть отрицательным числом?

— может, если один из векторов имеет отрицательные координаты

+ может, если угол между векторами тупой

— может, если вектора расположены в разных координатных четвертях

17. Чему равен косинус угла между векторами?

— сумме модулей векторов и их скалярного произведения

+ отношению скалярного произведения векторов к произведению их длин

— квадратному корню из скалярного произведения векторов

— произведению модулей векторов

18. Координаты двух векторов равны и . Необходимо найти косинус угла между этими векторами.

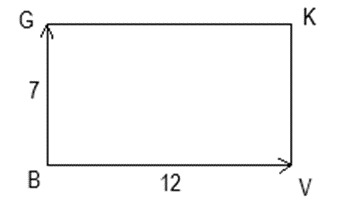
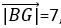
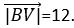
19. Дан прямоугольник GKVB. Известно, что длина вектора , а длина вектора Найдите скалярное произведение этих векторов.

тест-20. В треугольнике GBK стороны GB и BK равны, угол BGK=60 o , а сторона GK=6 см. Найдите скалярное произведение векторов

21. Скалярное произведение векторов, выраженных своими координатами, вычисляется как:

— произведение всех координат на синус угла между векторами

— произведение квадратов всех координат

— квадратный корень из произведения их координат

+ сумма попарного произведения их координат

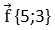
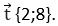
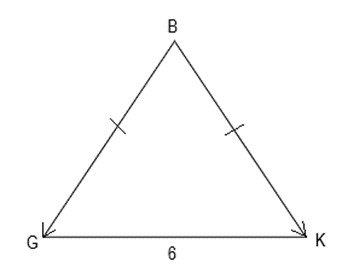
22. Даны два вектора с координатами. Вектор и вектор Найдите скалярное произведение этих векторов.

23. Даны три точки F, K и G с их координатами. По данным рисунка найдите косинус угла K.

24. Скалярный квадрат вектора равен… Закончите утверждение:

— произведению его координат

+ квадрату его длины

— квадратному корню из его модуля

— половине его длины, возведенной в квадрат

25. Выберите верное утверждение:

— скалярное произведение вектора самого на себя может быть отрицательным

— скалярное произведение вектора на самого себя не может быть равно нулю

+ скалярное произведение вектора самого на себя всегда больше или равно нуля

— все утверждения неверны

26. Найдите скалярный квадрат вектора с модулем 6 и координатами .

Содержание

Геометрия. 9 класс
Нахождение угла между векторами
Нахождение угла между векторами
📺 Видео

Видео:Как находить угол между векторамиСкачать

Геометрия. 9 класс

Выберите верные утверждения.

Скалярный квадрат вектора равен квадрату его длины.

Скалярным произведением двух векторов называется произведение длин двух векторов на косинус угла между ними.

Векторы перпендикулярны, если их скалярное произведение равно 0.

Скалярный квадрат вектора равен его длине.

Скалярным произведением двух векторов называется произведение длин двух векторов на синус угла между ними.

Если скалярное произведение векторов равно 0, то векторы перпендикулярны.

Выберите правильный ответ.

Найдите угол между векторами .

Выберите правильный ответ.

Угол между векторами равен 110°. Найдите угол между векторами .

Впишите верный ответ.

Чему равно скалярное произведение векторов , если , , угол между ними 60°?

Выберите правильный ответ.

Чему равно скалярное произведение векторов ?

Выберите правильный ответ.

Чему равен угол между векторами , если , , а ?

Впишите верный ответ.

В равностороннем треугольнике АВС сторона равна 6 см. Найдите .

Выберите верные утверждения.

Сторона квадрата АВСD равна 4.

Видео:Угол между векторами. 9 класс.Скачать

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Видео:Угол между векторами | МатематикаСкачать

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу: