3 д модель треугольника (3 видео) | Курс школьной геометрии

3D своими руками. Часть 4: треугольник невидимка

Содержание

Все части
Почему 3D-движки в основном используют треугольники для рисования поверхностей?
3 ответов
Руководства по топологии
6 советов моделирования с подразделением меша
📸 Видео

Видео:оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How to make Paper PyramidСкачать

Все части

Часть 2: оно трехмерное
( система координат, точка, вектор, матрица, вершина, индекс, конвейер визуализации )

Часть 4: треугольник невидимка
( треугольный полигон, нормаль )

В этой части мы разберем как и зачем строить модель при помощи треугольников. А также научимся не рисовать те части модели, которые не смотрят в камеру и не должны быть видны.

Для начала возьмите код с усеченной пирамидой из прошлой части бонусного раздела ( 25.01.22 в прошлую часть я внес исправления ошибок в код и текст, и если вы скачивали код раньше, нужно его сказать заново, какие именно правки указаны в конце прошлой части ). Всю пирамиду мы построили при помощи вершин ( массив vertices ) и ребер ( массив edges ). У этого подхода есть минус, у нас в коде у фигуры нету граней, т.е., у пирамиды неясно какие ребра ( или просто линии ) нужно соединить, чтобы в коде стало понятно что это грань, давайте посмотрим на такой пример

Индексы вершин усеченной пирамиды

По картинке видно что верхняя грань пирамиды это 0, 1, 2, 3 , лицевая грань: 3, 2, 6, 7 и т.д. Т.е. визуально мы эти грани различаем, но в коде у нас это никак не определено, т.к. мы рисуем фигуру линиями ( ребра ). Вы можете подумать, зачем нам вообще нужны грани, ведь и так красиво. Вопрос хороший и тут есть много причин, мы разберем некоторые из них.

Нам нужно знать грани, чтобы закрашивать модель в цвет, освещать её, или накладывать текстуры ( это будет в след. частях ). Ведь мы сейчас можем поменять цвет линии которой рисуем. А для того чтобы что-то закрасить, у нас должна быть замкнутая фигура в коде, которую будем заливать цветом.

Также грани нужны чтобы удалять невидимые части фигуры и немного оптимизировать скорость вывода и модель на экране была более реалистична ( посмотрим в этой части ).

Многие из моделей которые делают в других редакторах, состоят не просто из линий как наша текущая пирамида, а из множества граней ( полигонов ), которые стоят рядом и создают фигуру. Умение работать с такими моделями позволит нам в коде не создавать модели вручную ( их вершины и полигоны ), а загружать их из файлов, который были экспортированы из 3D-редакторов или скачаны из сайтов с 3D-моделями.

Давайте разберемся как нашу текущую модель и код переписать так, чтобы она имела понятия полигона. Первое что нам нужно это придумать систему, по которой мы будем выводить любую другую фигуру, а не только пирамиду. Ведь мы же не будем писать отдельную программу для пирамиды, сферы, или игрового персонажа… Например, смотря на пирамиду, мы видим что она состоит из 6 четырехугольных граней, у которых есть общие вершины. Все эти четырехугольники мы видим на картинке выше, там где пронумерованы вершины. Эти четырехугольники можно еще назвать четырехугольными полигонами. Но в 3D программировании на первых этапах нам проще использовать треугольные полигоны ( треугольники ), потому что такие полигоны будут в моделях, которые мы будем загружать из файлов. Плюс треугольники создают одну плоскость, в отличии от четырехугольника, и нам по треугольнику будет проще считать нормали ( узнаем что это в этой части ) и проще текстурировать ( разберем в следующих частях ). Вот пример треугольного и четырехугольного полигона:

Слева — треугольный полигон, справа — четырехугольный.

Из картинки можно увидеть что четырехугольный полигон, может создавать 2 плоскости. С треугольником такого не произойдет.

Для того чтобы начать использовать треугольники, нам много менять в уже имеющемся коде не придется.

Первое что нужно понять, что вершины никуда не деваются, все те же 8 штук, только теперь мы их соединим не просто линиями независимыми друг от друга, а каждую линию будем объединять в треугольник, так, чтобы получилась желаемая нам фигура. Принцип объединения такой-же как и был в массиве edges , т.е. при помощи индексов вершин, только теперь в массиве у нас будут не пары вершин ( пара т.к. у каждой линии есть начала и конец ), а по 3 вершины, например, чтобы описать 1 треугольник нам нужно указать 3 вершины, соединив которые мы получим треугольник. Мы уже упоминали что для построения усеченной пирамиды нам нужно 6 четырехугольников, а вот треугольников нам нужно в 2 раза больше, т.к. для вывода одного четырехугольника ( четырехугольного полигона ) нужно 2 треугольника. На картинке ниже в верхней части мы выводим 1 сторону пирамиды при помощи линий ( как у нас сейчас ), а ниже при помощи треугольников ( так сделаем ). В результате и там и там у нас визуально получился четырехугольник ( например, грань пирамиды ). Но в случае треугольников, у нас еще есть линия по диагонали, т.к. по сути это 2 приставленных к друг другу треугольника. Эта линия видна только потому что мы рисуем линиями. Когда мы научимся закрашивать в цвет, а потом и текстурировать фигуры и отключим линии, их не будет видно, и все будет выглядеть красиво, без ненужных стыков:

Сверху прямоугольник из линий, снизу — из треугольников.

Кажется что использование треугольников – избыточно. Конкретно в этом случае так и есть, т.к. пирамида состоит из четырехугольников и тут они конечно больше подходят. Но вспомните о преимуществах, которые описаны выше. А также о том, что мы не будем все время выводить одни пирамиды, будут другие, более сложные фигуры, где треугольники уже покажутся лучшим выбором и чтобы в коде все было просто и все фигуры выводились одинаково, мы все их будем выводить при помощи треугольников, хоть это и будет иногда не самым идеальным вариантом.

Давайте закомментируем массив edges и заменим его на массив indices , в котором будут подмассивы по 3 индекса:

В этом массиве каждая строчка ( подмассив из 3х элементов ) – это 3 индекса из массива вершин ( vertices ) которые если мы соединим линиями между собой – получим треугольник. Таким образом мы описали все стороны усеченной пирамиды, их у нее 6, но они прямоугольные, и для каждого прямоугольника приходится использовать по 2 треугольника.

Теперь нужно переписать код отрисовки линий, т.к. теперь мы рисуем не по одной линии используя массив edges , а сразу будем выводить по треугольнику ( массив indices ).

Давайте закомментируем целиком цикл работы с edges :

И вместо него будем перебирать массив indices :

Внутри этого цикла при помощи записи indices[i] мы можем достать строчку с 3мя индексами конкретного выводимого треугольника, эти индексы указывают на вершины в массиве sceneVertices ( т.к. мы сохранили порядок вершин из оригинального массива indices ). Поэтому при помощи такой записи мы можем достать координаты всех вершин:

И последним шагом перехода на треугольники — отрисовка 3х линий по 3м точкам:

В каком порядке рисовать линии не имеет значения, главное чтобы все 3 точки были соединены между собой и на экране получился треугольник.

Для того чтобы видеть пирамиду в динамике, давайте вернем ей вращение по оси Y , сразу после вращени по X ( хоть там сейчас и 0 стоит для X ):

Если все сделали правильно, то у вас должна быть на экране вращающаяся пирамида состоящая из треугольников:

Модель усеченной пирамиды из треугольников

Как видите, она отличается от предыдущей наличием диагональных линий, как я уже упоминал ранее это потому что каждый четырехугольник в пирамиде состоит из рядом стоящих 2 треугольников. Такой артефакт мы позднее уберем, в следующих частях.

Теперь давайте посмотрим еще раз что не так. У пирамиды которая получилась как и всех моделей выводимых ранее видны сразу все её грани ( технически мы видим линии ребер, т.к. их рисуем ), ранее это нас устраивало, т.к. нужно было видеть что происходит с каждой стороны, настраивать перспективу и т.д.

Предлагаю сделать оптимизацию и скрыть те грани фигуры, которые нам не должны быть видны. Это даст более реалистичную картинку ( сделает пирамиду непрозрачной ), также мы немного ускорим приложение, т.к. не будем рисовать линии тех треугольников, что сейчас не должны быть видны.

Для того чтобы эти треугольники скрыть, давайте подумаем как вообще это можно сделать. Сейчас когда мы используем треугольники, мы знаем что у него есть одна плоскость с 2мя сторонами, если бы мы вырезали треугольник из бумаги, то можно было бы его покрутить то одно стороной то другой. В жизни мы конечно видим треугольник независимо от того какой стороной он к нам повернут, но в 3D графике мы можем настроить так, чтобы была видна только одна сторона. Как определить какая сторона должна быть лицевой и видимой? Вообще обе стороны имеют право на звание лицевой и тут свобода выбора, поэтому мы как разработчики этой модели сами должны решить, какая сторона какой будет. Сейчас мы не оперируем понятием сторона в коде, у нас есть только индексы 3х вершин, по которым мы рисуем линии. Для того чтобы это понятие появилось нам поможет очень полезная штука — нормаль. Нормаль это вектор перпендикулярный треугольнику и откуда исходит нормаль, та сторона и считается лицевой:

Нормаль видимой грани.

Синяя стрелка это вектор нормали для какого-то треугольника. Поскольку выше упоминалось что сторон у треугольника 2, то и нормали тоже может быть 2, но нам нужна только 1 нормаль, та которая будет исходить из видимой стороны треугольника. когда мы будем считать нормаль ( ниже покажу как это делать ) то мы будем считать ее при помощи уже имеющихся у нас 3х вершин треугольника и порядок расстановки вершин будет влиять на то в какую сторону указывает нормаль. Например, если бы точки a, b, c дали бы нам одну нормаль, то c, b, a дали бы уже другую, возможно, в противоположную сторону. Следить за массивом indices вручную очень сложно, ведь у нас очень простая фигура и там уже 12 записей по 3 индекса. Поэтому все это за нас уже давно делают 3D редакторы, когда мы экспортируем модели из них, они уже расставляют вершины в правильном всегда одинаковом порядке, так что мы сможем по ним посчитать правильные нормали. Но пока мы с 3D-редакторов еще не умеем что либо загружать, я правильную расстановку вершин в массиве indices уже сделал заранее, тот массив что мы использовали выше расставлен так, что все индексы вершин в нем дают нам правильные нормали.

Для того чтобы посчитать сами нормали нам никаких новых методов добавлять не придется, более того, мы уже делали их в прошлой части в секции бонуса, когда считали вектор для движения в сторону по отношению к положению к камере.

Для того чтобы посчитать нормаль. нам нужно получить 2 вектора треугольника, именно эти вектора образуют плоскость, перпендикуляр к которой мы хотим получить — это и будет нормалью, чтобы получить из 3х точек 2 вектора, нам нужно применить уже известную функцию substruct , ведь если вычесть одну точку из другой, мы получим вектор направления от одной точки к другой. Добавьте следующий код ниже получения v1, v2, v3 в цикле перебора indices :

И теперь вектора t1 и t2 образуют плоскость, если мы перемножим их при помощи векторного произведения векторов, то получим вектор перпендикулярный обоим векторам — это и будет нашей нормалью:

Порядок вычитания точек играет роль, в примере выше если бы я отнимал v2 и v1 ( вот так: let t1 = Vector.substruct(v2, v1); ) то вектор был бы у меня в другом направлении, и это могло бы дать нормаль в другом направлении, в таком случае я увижу внутреннюю часть пирамиды. Вообще тут строго запоминать какие вектора от каких отнимать и не нужно, вы всегда можете подобрать порядок вычитания так — как вам нужно. Получили не тот результат и фигура наизнанку, поменяйте вектора местами и получить то что вам нужно. Ведь тут нельзя говорить что если нормаль повернута в другую сторону то это неправильно, т.к. вполне может быть что мы хотим такое отображение для игры, например, если нам нужно сделать простенький горизонт в игре, для этого мы можем поместить сферу вокруг нашей камеры и наложить текстуру на внутреннюю сторону сферы, т.к. мы видим её изнутри, и тут нормали, возможно, нам придется направить в другую сторону переставив вектора местами или любым другим способом. В тоже время эту же модель сферы мы можем переиспользовать для других объектов в игре и там уже нам нужно отрисовывать наружную часть сферы, где нормали повернуты в противоположную сторону от тех что нужны были для горизонта. Таким образом для одной модели нам может понадобиться считать нормали направленные как в одну сторону, так и в другую, зависимо от того что мы хотим получить на экране. А может нам и вовсе не нужно делать какую-то часть треугольника невидимой, если мы хотим чтобы были видны обе его стороны.

Нормали нужны далеко не для того чтобы можно было посчитать какие полигоны ( треугольники ) модели видны, с помощью нормалей, например, можно освещать модели, но это мы сделаем в следующих частях.

Теперь, когда у нас есть нормаль треугольника, нужно посчитать должен ли этот треугольник быть видимым по отношению к камере ( с нашего ракурса ). Для этого мы можем воспользоваться новой операцией над векторами: скалярным произведением векторов. Для этой операции нам нужно 2 вектора и в результате этой операции мы получим число, которое на первый взгляд не понятно как применить к нашей задаче. Определение результата скалярного произведения векторов звучит так: результатом называется число, равное произведению длин этих векторов на косинус угла между ними. Что за длины, что за косинус и как нам все это поможет? Давайте разбираться, добавим код этого самого скалярного произведения в класс Vector :

Код не сложный, а вот определение результата так себе. На самом деле нам в результате этой операции само число и не нужно, нам нужен лишь знак этого числа. Ведь в формулировке говорится что результат это длины векторов и косинус угла между ними перемноженные между собой, вот длины векторов нам не особо нужны, они всегда положительные, а вот косинус угла как раз интересный, т.к. если вспомним чуть математику или просто брутфорсом начнем подставлять углы в косинус, то увидим, что косинус угла 90 градусов = 0 , а косинус 89 градусов равен примерно 0.017 , а косинус 91 градуса -0.017 . Т.е. если угол который мы передадим в косинус более 90 градусов то мы будем получать отрицательные числа, а если менее — положительные. Таким образом, если результат скалярного произведения векторов окажется положительным, то значит что угол между ними ( в нашем случае между вектором камеры и нормалью треугольника ) менее 90 градусов и такой треугольник нам нужно рисовать, а если отрицательный — не нужно. Т.е. мы не зная углов между камерой и нормалью все равно можем принимать решения по отрисовке, т.к. в результате хоть и нету угла, но есть косинус угла, который даст нам правильный знак в результате скалярного произведения. Давайте попробуем это теперь применить в коде, ниже строчки в которой мы посчитали нормаль, добавим скалярное произведения вектора камеры на нормаль:

И следующей строчкой, поместим всю отрисовку пирамиды в проверку:

Если все сделали правильно, у Вас должна получиться пирамида, у которой видна только часть смотрящая в камеру, а остальные грани отброшены условием.:

Такое отсечение невидимых граней еще называют отбраковкой обратной стороны ( или backface culling ). Для теста, можете заменить в условии res > 0 на res и увидите внутреннюю часть пирамиды, т.к. теперь мы рисуем отвернутые от камеры треугольники.

На этом часть заканчивается, но приключение продолжается! В этот раз мы научились выводить модель при помощи треугольников. Посмотрели как считать нормали и как при помощи этих нормалей скрывать невидимую часть фигуры, воспользовавшись новой операцией, скалярным произведением векторов.

В следующей части мы посмотрим как можно закрашивать треугольники в интересующий нас цвет, научимся отсекать слишком близкие и далекие пиксели ( используем near / far параметры матрицы перспективы ) а также познакомимся с z-буфером, при помощи которого будем рисовать пиксели нескольких моделей на экране так, чтобы они правильно перекрывали друг друга. И даже сделаем первую игру, используя уже имеющиеся знания и наработки.

Видео:КАК СДЕЛАТЬ ТРЕУГОЛЬНИК 3D ОРИГАМИ | ОБЪЕМНЫЙ ТРЕУГОЛЬНИК | КОРОБОЧКА ОРИГАМИСкачать

Почему 3D-движки в основном используют треугольники для рисования поверхностей?

Почему треугольники всегда используются для рисования поверхностей в 3D? Почему не квадрат или какую-нибудь другую форму?

Видео:Пирамида из бумаги/Paper pyramid/DIYСкачать

3 ответов

треугольники никогда не могут быть неплоскими; все, что имеет более 3 точек, может быть неплоским и, следовательно, не может быть отображено, если не преобразовано в треугольники.

например: квадрат-это два треугольника, которые находятся на одной плоскости, если все точки, составляющие квадрат, являются планарными. Требуется много вычислений, чтобы убедиться, что все точки являются со-планарными, поэтому все полигоны, которые больше 3 точек, предварительно вычисляются путем их прореживания в треугольники и проверяются, чтобы убедиться, что все точки являются планарными один раз, а не на каждом кадре, который получает визуализацию.

Плоская Сетка

Неплоская Сетка

и еще один пример, что может сделать это яснее!—1—>

неплоская сетка вырождается и не может быть отсортирована или отображена правильно в любом здравом уме. Треугольники не имеют этой проблемы.

эффективность

треугольники также очень эффективны в памяти и могут быть отсортированы и визуализированы очень быстро при использовании треугольник Полоски которому нужно только 1 пункт, который нужно сохранить для каждого дополнительного треугольника после первого.

и Фанаты Треугольник что является частным случаем треугольной полосы.

поскольку 3 точки являются минимальными, необходимыми для определения плоской поверхности, любая форма может быть смоделирована с использованием многих треугольников, и существуют эффективные алгоритмы для быстрого рисования треугольников на экране.

в основном любая сложная (поверхностная) структура может быть представлена в виде пучка треугольников. Треугольник — это самая атомарная и примитивная геометрия. Поэтому он используется как основа почти для чего угодно. Тем не менее, большинство 3D-двигателей предоставляют вам более сложные примитивы, такие как сферы, конусы, цилиндры, пончики, что угодно. Проверьте документацию библиотек.

Видео:Как сделать ромб из бумаги. Оригами ромб из бумагиСкачать

Руководства по топологии

6 советов моделирования с подразделением меша

Вот несколько советов по моделированию объектов с помощью модификатора Subdivision Surface:

1. Всегда начинайте с построения блочной модели

Создание блочной модели является одним из наиболее важных этапов моделирования. На этом этапе вы определяете масштаб, стиль и внешний вид вашей модели. Вот почему вы должны всегда начинать с базовой формы. Если же вы начинаете добавлять много деталей, то изменить дальнейшую форму меша будет достаточно проблематично.

2. Используйте настолько мало полигонов, насколько это возможно

Когда вы подразделяете меш с помощью модификатора Subdivision Surface вам не стоит больше беспокоится об острых углах вашего объекта, потому как все они будут сглажены. В итоге никто не увидит изначальную «low-poly» модель. Вам действительно нужно использовать цилиндр с 32-я ребрами или можно обойтись и 6-ю добавив модификатор Subdivision Surface в уровень 2? Создавайте ваши модели как можно более простыми. Если полигоны не выполняют конкретную задачу, то, скорее всего, они должны быть удалены.

3. Треугольники (tris) и многоугольники (N-gons) не всегда плохо

Треугольники и многоугольники имеют довольно отвратительную репутацию, потому как во многих случаях портят топологию объекта, но если их использовать в правильных обстоятельствах, они могут быть полезны. В итоге они все равно будут преобразованы в четырехугольники. Только не воспринимайте данные слова как разрешение на использование треугольников и многоугольников где угодно, потому как плохая репутация у них возникла не на пустом месте, но в некоторых случаях их применение может быть более предпочтительным, нежели четырехугольников.

4. Сохраняйте квадратную форму четырехугольников

Вы вероятно слышали это правило уже много раз, но до сих пор встречается огромное количество моделей, в которых четырехугольники имеют прямоугольную форму. Это одно из фундаментальных правил, которое должно соблюдаться при моделировании. Соблюдение этого правила позволит сделать вашу модель более гладкой, а также избежать различных проблем при создании UV-развертки.

5. Моделируйте с использованием модификаторов

Модификаторы не изменяют топологию ваших объектов. Вы можете включать/выключать их в любой момент без каких-либо последствий для исходного меша. Использование модификаторов вместо прямого изменения топологии значительно предпочтительнее и сэкономит вам не один час времени.

6. Используйте складки (Creases) на небольших или удаленных объектах

Вместо того, чтобы добавлять дополнительные ребра для придания жесткости тем или иным частям меша используйте инструмент Crease. Это позволит сохранить небольшое количество полигонов на вашем объекте и его простоту. Как сказано в заголовке, используйте этот прием на маленьких объектах, либо тех, что находятся далеко от камеры.

Быстрый метод создания квадратных панелей: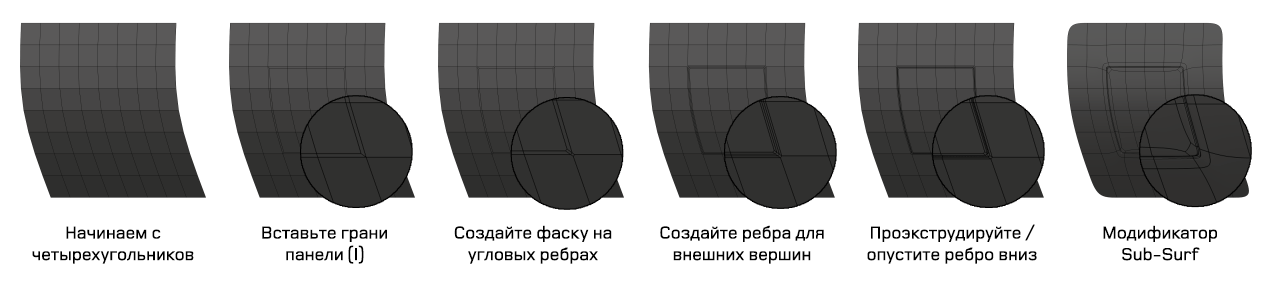

Изменение направления ребра (loop cut) меша: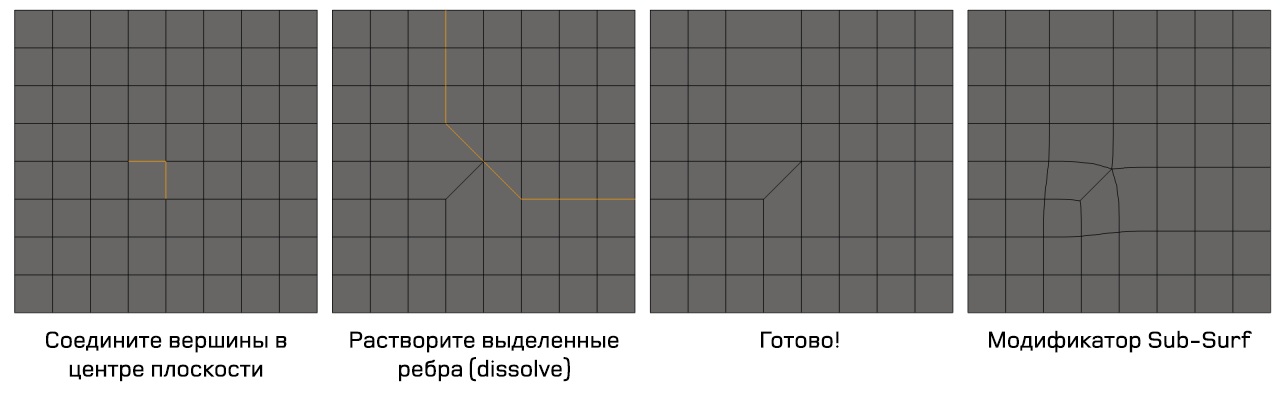

Различные типы углов:

Короткий урок по созданию микрометрического винта. Прошу прощения у пользователей Autodesk, этот метод работает только в Blender 🙂

Создание T-образного соединения труб:

Создание изогнутых углов:

Различные типы создания фасок:

Еще один короткий урок. Не знаю, как назвать эту форму, но я видел ее на множестве объектов:

Три типа закругленных цилиндров: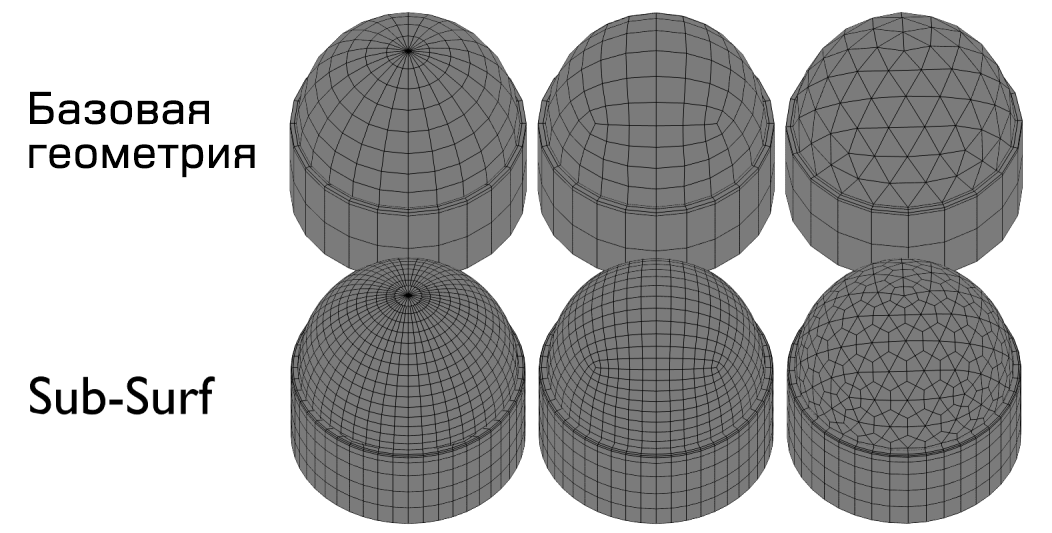

Пять типов крышек цилиндров. Нижняя строка модификатор Subdivision Surface с уровнем 1: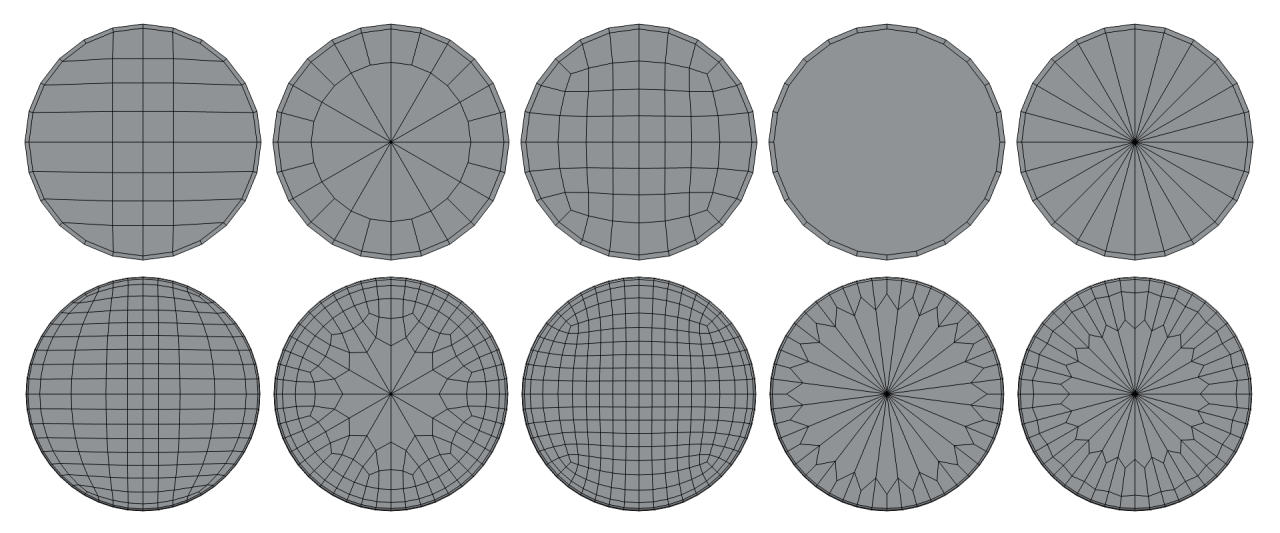

Добавление отверстий на плоской поверхности: