Контрольная работа # 2 по геометрии в 10 классе (базовый уровень) «Параллельность в пространстве» для УМК Мерзляк, Номировский, Поляков, под ред. В. Е. Подольского в 4-х вариантов. Геометрия 10 Контрольная 2 Мерзляк. Ответов нет.
- Геометрия 10 класс (УМК Мерзляк) Контрольная работа № 2
- Вариант 1
- Вариант 2
- Вариант 3
- Вариант 4
- Добавить комментарий Отменить ответ
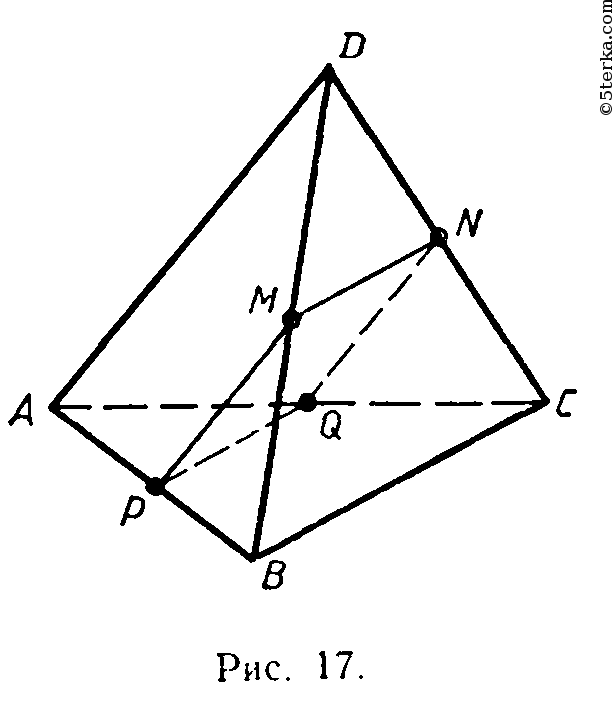
- 17. На рисунке 17 точки М, N, Q и Р — середины отрезков DB, DC, АС и АВ. Найдите периметр четырехугольника MNQP, если AD= 12 см, ВС =14 см.
- Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB?
- В прямоугольном параллелепипеде ABCDA1B1C1D1 точки O и E — середины отрезков AB1 и AC соответственно?
- Диагонали квадрата ABCD пересекаются в точке O, точка F — середина стороны CD, а точка T лежит на стороне AD и TF / / AC?
- В ромбе ABCD диагонали пересекаются в точке О?
- В четырёхугольнике MNPQ точки А В С D, соответственно, середины сторон MN NP PQ QM?
- Дан квадрат ABCD?
- Отрезок AC в 3 раза больше отрезка CD?
- Отрезок AC в 3 раза больше отрезка CD найдите отношение BC : AD если точка B середина отрезка AD?
- В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и AD соответственно?
- Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB?
- Отрезки АВ и CD параллельны и равны?
- 🎦 Видео
Геометрия 10 класс (УМК Мерзляк)
Контрольная работа № 2
Параллельность в пространстве
Вариант 1
- Точки M, N, P и Q — середины отрезков BC, BD, AD и AC соответственно, AB = 14 см, CD = 18 см (рис. 9). Определите вид четырёхугольника MNPQ и вычислите его периметр.
- Плоскость а пересекает стороны AB и BC треугольника ABC в точках M и K соответственно и параллельна стороне AC, MK = 4 см, MB : MА = 2 : 3. Найдите сторону AC треугольника.
- Треугольник ABC является изображением правильного треугольника A1B1C1 (рис. 10). Постройте изображение высоты треугольника, опущенной на сторону AC1.
- Плоскости а и b параллельны. Из точки M, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости a и b в точках А1 и B1, а другой — в точках А2 и B2 соответственно. Найдите отрезок В1В2, если он на 2 см больше отрезка А1А2, МВ1 = 7 см, А1B1 = 4 см.
- Точки A, B, C, не лежащие на одной прямой, являются параллельными проекциями трёх последовательных вершин правильного шестиугольника. Постройте изображение этого шестиугольника.
Вариант 2
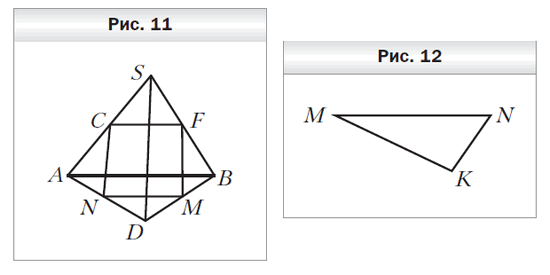
- Точки F, M, N и C — середины отрезков BS, DB, AD и AS соответственно, SD = 30 см, AB = 36 см (рис. 11). Определите вид четырёхугольника FMNC и вычислите его периметр.
- Плоскость b пересекает стороны AB и AC треугольника ABC в точках N и D соответственно и параллельна стороне BC, AD = 6 см, DN : CB = 3 : 4. Найдите сторону AC треугольника.
- Треугольник MNK является изображением правильного треугольника M1N1K1 (рис. 12). Постройте изображение биссектрисы треугольника, проведённой из вершины M1.
- Плоскости а и b параллельны. Через точку M, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости а и b в точках А1 и B1, а другая — в точках А2 и B2 соответственно. Найдите отрезок А1А2, если он на 1 см меньше отрезка B1B2, MA2 = 4 см, А2B2 = 10 см.
- Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин квадрата и его центра. Постройте изображение квадрата.
Вариант 3
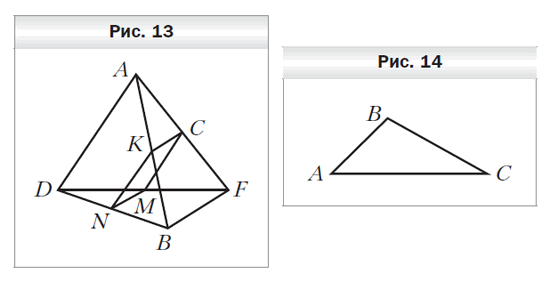
- Точки N, M, C и K — середины отрезков BD, DF, FA и AB соответственно, BF = 24 см, AD = 18 см (рис. 13). Определите вид четырёхугольника NMCK и вычислите его периметр.
- Плоскость а пересекает стороны MF и MK треугольника MFK в точках A и B соответственно и параллельна стороне FK, AB = 12 см, AM : AF = 3 : 5. Найдите сторону FK треугольника.
- Треугольник ABC является изображением правильного треугольника А1B1C1 (рис. 14). Постройте изображение центра вписанной окружности треугольника А1B1C1.
- Плоскости а и b параллельны. Из точки O, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости а и b в точках C1 и D1, а другой — в точках C2 и D2 соответственно. Найдите отрезок C1C2, если он на 5 см меньше отрезка D1D2, OC1 = 4 см, C1D1 = 10 см.
- Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин правильного треугольника и его центра. Постройте изображение этого треугольника.
Вариант 4
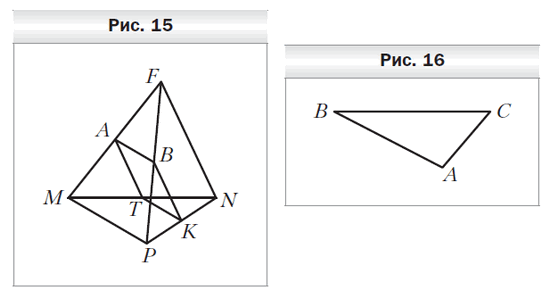
- Точки A, B, K и T — середины отрезков MF, PF, PN и MN соответственно, MP = 10 см, FN = 16 см (рис. 9). Определите вид четырёхугольника ABKT и вычислите его периметр.
- Плоскость b пересекает стороны CF и CD треугольника CDF в точках M и N соответственно и параллельна стороне FD, MN = 6 см, FD = 21 см, MC = 10 см. Найдите сторону FC треугольника.
- Треугольник ABC является изображением правильного треугольника А1B1C1 (рис. 16). Постройте изображение центра описанной окружности треугольника А1B1C1.
- Плоскости а и b параллельны. Через точку D, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости а и b в точках M1 и N1, а другая — в точках M2 и N2 соответственно. Найдите отрезок M1M2, если он на 8 см больше отрезка N1N2, N1M1 = 30 см, DN1 = 5 см.
- Точки A, B и M, не лежащие на одной прямой, являются соответственно параллельными проекциями двух соседних вершин параллелограмма и середины его противолежащей стороны. Постройте изображение этого параллелограмма.
Вы смотрели: Контрольная работа по геометрии в 10 классе (базовый уровень) «Параллельность в пространстве» для УМК Мерзляк, Номировский, Поляков, под ред. В. Е. Подольского в 4-х вариантов. Геометрия 10 Контрольная 2 Мерзляк. Ответов нет.
(с) Цитаты из пособия «Математика : алгебра и начала математического анализа, геометрия. Геометрия. Базовый уровень : 10 класс : методическое пособие / Е. В. Буцко, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. — М.: Вентана-Граф» использованы в учебных целях.
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Видео:№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
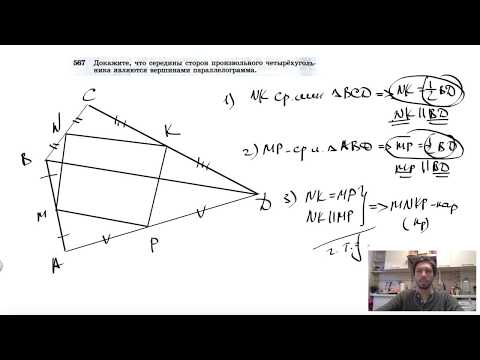
17. На рисунке 17 точки М, N, Q и Р — середины отрезков DB, DC, АС и АВ. Найдите периметр четырехугольника MNQP, если AD= 12 см, ВС =14 см.
по теореме п. 5 получим: PM || QN.
Отсюда следует, что P, Q, M и N лежат в 1 плоскости.
Получим, что MN и PQ — средние линии в ΔBDC и ΔABC, значит, MN || BC и PQ || BC. Имеем из теоремы п. 5 MN || PQ.
Значит, 4-угольник MNPQ — параллелограмм по определению (т.к. является плоским четырехугольником).

задача №17
к главе «Глава I Параллельность прямых и плоскостей. §1 Параллельность прямых, прямой и плоскости.».
Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB?
Геометрия | 10 — 11 классы
Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB.
Вычислите периметр четырёхугольника MNPQ, если AC = 11 см и BD = 18 см.
Ну тут не трудно заметить, что отрезки MQ, QP, NP и MP — средние линии треугольников.
MQ и NP — среднии линии треугольников ADB и BDC соотвественно, и BD — общее основание, значит MQ = NP, а MQ = 1 / 2 * BD, MQ = 9см = NP
Проворачиваем такие же махинации с треугольниками ABC и ADC, там будет сторона 5, 5, ну и периметр тогда = 2 * 9 + 5, 5 * 2 = 29см.
Видео:№166. Отрезки АВ и CD пересекаются в их общей середине О. Точки М и N — середины отрезков АС и BD.Скачать

В прямоугольном параллелепипеде ABCDA1B1C1D1 точки O и E — середины отрезков AB1 и AC соответственно?
В прямоугольном параллелепипеде ABCDA1B1C1D1 точки O и E — середины отрезков AB1 и AC соответственно.
Вычислите длину отрезка OE, если AD = 3 см, DD1 = 4 см.
Видео:№537. Отрезок AD является биссектрисой треугольника ABC. Найдите BD и DC, если АВ = 14 смСкачать

Диагонали квадрата ABCD пересекаются в точке O, точка F — середина стороны CD, а точка T лежит на стороне AD и TF / / AC?
Диагонали квадрата ABCD пересекаются в точке O, точка F — середина стороны CD, а точка T лежит на стороне AD и TF / / AC.
Вычислите площадь четырёхугольника AOFT, если AB = 6 см.
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

В ромбе ABCD диагонали пересекаются в точке О?
В ромбе ABCD диагонали пересекаются в точке О.
P. K — середины отрезков CD.
OC. OB соответственно.
Вычислите периметр четырехугольника OKPF.
Если периметр ромба равен 32 см.
Видео:№121. Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC. а) Докажите, что ΔСВОСкачать

В четырёхугольнике MNPQ точки А В С D, соответственно, середины сторон MN NP PQ QM?
В четырёхугольнике MNPQ точки А В С D, соответственно, середины сторон MN NP PQ QM.
Найдите сумму АВ + СD, если МР равен 50см.
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Дан квадрат ABCD?
Дан квадрат ABCD.
Точки MNPQ являются серединами его сторон.
Укажите вид четырехугольника MNPQ.
Видео:Построение середины отрезкаСкачать

Отрезок AC в 3 раза больше отрезка CD?
Отрезок AC в 3 раза больше отрезка CD.
Найдите отношение BC : AD если точка B середина отрезка AD.
Видео:Длина отрезкаСкачать

Отрезок AC в 3 раза больше отрезка CD найдите отношение BC : AD если точка B середина отрезка AD?
Отрезок AC в 3 раза больше отрезка CD найдите отношение BC : AD если точка B середина отрезка AD.
Видео:№129. Отрезки АС и BD пересекаются в середине О отрезка AC, ∠BCO = ∠DAO. Докажите, что ΔВОА=ΔDОС.Скачать

В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и AD соответственно?
В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и AD соответственно.
Ребят, очень нужна ваша помощь!
Площади четырёхугольников ABLN и NLCD равны, а площади четырёхугольников KBCM и AKMD относятся как 11 : 17.
А) Докажите, что прямые BC и AD параллельны.
Б) Найдите отношение BC к AD.
Видео:№142. Концы отрезка отстоят от плоскости α на расстояниях 1 см и 4 см. Найдите расстояниеСкачать

Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB?
Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB.
Вычислите периметр четырёхугольника MNPQ, если AC = 17 см и BD = 17 см.
Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Отрезки АВ и CD параллельны и равны?
Отрезки АВ и CD параллельны и равны.
Докажите, что точка К является серединой отрезка ВС.
На этой странице находится ответ на вопрос Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB?, из категории Геометрия, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.
Угол АОФ = 180° — ( угол АОВ + угол ВОС).
1 вершина под больше вершины под БКР.
Площадь параллелограмма S = H * a не указано на какую сторону опущена высота двойной ответ S = 2 * 3 = 6 см2 S = 2 * 8 = 16 см2 сделайте рисунок и вы поймете.
Р = 2 * (a + b) Отношение разбивает стороны на части. Пусть х м длина одной части. Тогда а = 3х, b = 4x P = 2 * (3x + 4x) = 2, 8 14x = 2, 8 x = 2, 8 : 14 x = 0, 2 3 * 0, 2 = 0, 6(м) длина одной стороны 4 * 0, 2 = 0, 8(м) длина другой стороны. Отве..
920 : 4 = 230 za 1 chas 230umnojit na 5 = 1150 230 : 60 = 38.
4×4 = 16 кв ед — площадь ромба .
S = (AB * AC) / 2 Дальше посчитай.
40 + 6 40 * 3 = 120 6 * 3 = 18 120 + 18 = 138 30 + 8 30 * 7 = 210 8 * 7 = 56 210 + 56 = 266.
Треугольники СNK и АВС подобны с коэффициентом подобия 20 : 25 = 4 : 5 СN : AC = 4 : 5 24 : AC = 4 : 5 AC = 30. На отсутствующем в условии рисунке, точка N должна лежать на стороне АС ).
Ответ : В = 12 А. Объяснение : Обозначим вершины целого треугольника АВС, закрашенной части –ЕКС. Примем площадь ∆АВС = S. Проведем отрезок АМ к середине ВС. Медиана делит площадь треугольника на треугольники с равной площадью. ⇒ Площадь ∆ АМС =..
🎦 Видео
№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть I)Скачать

Множества и операции над нимиСкачать

№320. В тетраэдре ABCD точки М, N и К— середины ребер АС. ВС и CD соответственноСкачать

Решение задачи №1 из ЕГЭ математикаСкачать
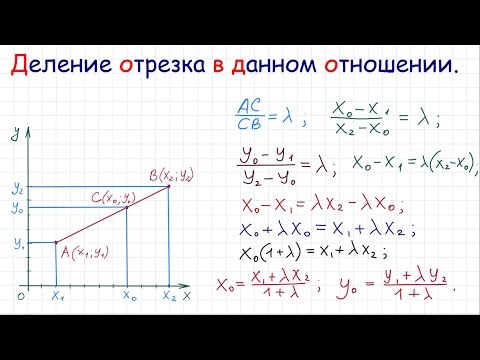
Деление отрезка в данном отношенииСкачать
Разбор 4 задания | ОГЭ по информатике 2021Скачать

1707 точка M и N являются серединами сторон AB и BC треугольника ABCСкачать