Видео:№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать
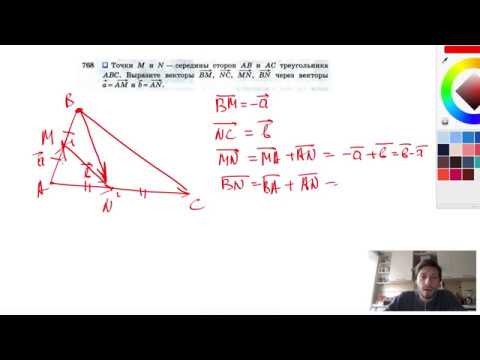
Ваш ответ
Видео:№432. Точки М и N — середины сторон AD и ВС параллелограмма ABCD. Докажите, что прямыеСкачать
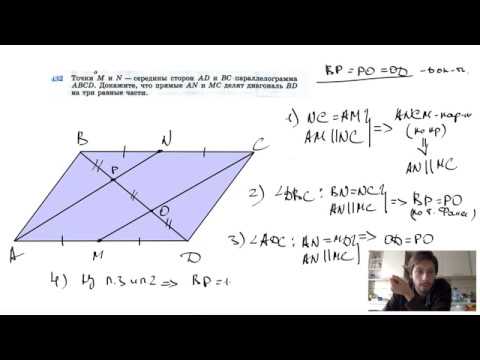
решение вопроса
Видео:Геометрия Точки M, N, K и P – середины сторон AB, BC, CD и AD параллелограмма ABCD соответственноСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,754
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
Повторение. Решение задач (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |
1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу.
2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264.
IV. Решение задач.
1. Решить задачу 2. Точки M и N – середины сторон AB и CD четырехугольника ABCD. Докажите, что 
Пусть О – произвольная точка. Согласно задаче 1 из п. 84 имеем 
поэтому 
.
Примечание. Результат задачи 2 можно использовать при доказательстве теоремы о средней линии трапеции на следующем уроке.
2. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ =
= 2 : 3. Докажите, что для любой точки О справедливо равенство
По условию AC : CB = 2 : 3, поэтому 
Но 
Следовательно, 
откуда получается
Примечание. Задача 3 является частным случаем более общей задачи 806.
3. Решить задачу № 000 на доске и в тетрадях.
4. Решить задачу № 000 на доске и в тетрадях.
Так как точка А1 – середина стороны ВС, то 
.
Далее 
5. При наличии времени решить задачу 4.
Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.
Пусть О – произвольная точка. Согласно задаче 1 из п. 84
.
Аналогично, 
.
Из этих равенств следует, что 
Отсюда следует, что PQ || AE и PQ = 
AE.
Домашнее задание: повторить материал пунктов 76–84; разобрать решения задачи 2 из п. 84 и задачи № 000 и записать в тетрадь; решить задачу № 000.
Урок 8
Средняя линия трапеции
Цели: ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов; упражнять учащихся в решении задач.
I. Проверка усвоения учащимися материала.
1. Устно ответить на вопросы:
1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы 
и 
и противоположно направленные векторы 
и 
.
2) Какой вектор называется произведением данного вектора на данное число?
3) Могут ли векторы и 
быть неколлинеарными?
4) Сформулируйте основные свойства умножения вектора на число.
2. Решить задачу на доске и в тетрадях по готовому чертежу:
Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC =
= 3 : 4.
Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.
Пусть K1 – середина AB, K2 – середина MN, K3 – середина CD. Согласно задаче 2 из п. 84 имеем
. Из условия следует, что 
, поэтому 
.
Таким образом, векторы 
и 
коллинеарны, и, значит, точки K1, K2 и K3 лежат на одной прямой.
II. Объяснение нового материала.
1. Определение трапеции. Виды трапеций.
2. Определение средней линии трапеции.
3. Доказательство теоремы о средней линии трапеции (проводит сам учитель).
При доказательстве теоремы целесообразно использовать результат задачи 2, решенной на предыдущем уроке.
Доказательство можно оформить на доске и в тетрадях в виде следующей краткой записи:
Дано: ABCD – трапеция, AD || BC, M – середина стороны AB; N – середина стороны CD (рис. 266 учебника).
Доказать: MN || AD, MN = 
.
1) Согласно рассмотренной в классе задаче 1 
.
2) Так как 
, то 
и, значит, MN || AD.
3) Так как , то 
= AD + BC, поэтому
MN = 
(AD + BC).
III. Закрепление изученного материала (решение задач).
1. Решить на доске и в тетрадях задачу № 000.
Пусть a и b – основания трапеции, тогда а + b = 48 – (13 + 15) =
= 20 (см); средняя линия MN = 
= 10 (см).
2. Решить задачу № 000.
3. Решить задачу № 000 на доске и в тетрадях.
Пусть BK – перпендикуляр, проведенный к основанию AD данной трапеции.
Но AK = 
, поэтому KD =
= AD –
, то есть
отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.
IV. Проверочная самостоятельная работа.
Точка K делит отрезок MN в отношении MK : KN = 3 : 2. Выразите вектор 
через векторы 
и 
, где A – произвольная точка.
Точка A делит отрезок EF в отношении EA : AF = 2 : 5. Выразите вектор 
через векторы 
и 
, где K – произвольная точка.
Домашнее задание: изучить материал пункта 85; ответить на вопросы 18–20, с. 214 учебника; решить задачи №№ 000, 794, 796.
Основные требования к учащимся:
В результате изучения параграфа учащиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 000–787; 793–799.
МЕТОД КООРДИНАТ (10 часов)
Урок 1
Разложение вектора по двум данным
неколлинеарным векторам
Цели: доказать лемму о коллинеарных векторах и теорему о разложении вектора по двум неколлинеарным векторам и закрепить их знание в ходе решения задач.
I. Анализ результатов самостоятельной работы.
II. Устная работа.
1. Устно решить задачи по заранее заготовленному чертежу на доске:
Дан параллелограмм ABCD с диагоналями AC и BD, пересекающимися в точке О, а также отрезки MP и NQ, соединяющие соответственно середины сторон AB и CD, BC и AD. Требуется выразить:
1) вектор 
через вектор 
;
2) вектор 
через вектор 
;
3) вектор 
через вектор 
;
4) вектор 
через вектор 
.
2. Вопрос учащимся:
можно ли для любой пары коллинеарных векторов подобрать такое число, что один из векторов будет равен произведению второго вектора на это число?
III. Изучение нового материала.
1. Формулировка леммы о коллинеарных векторах. Для понимания учащимися формулировки леммы полезно обсудить, во-первых, почему важно условие 
и, во-вторых, будет ли верно утверждение, если рассматривать произвольные (в том числе и неколлинеарные) ненулевые векторы.
2. Доказательство леммы.
3. Решить задачу по рисунку параллелограмма ABCD на доске (тем самым подвести учащихся к мысли о возможности выражения вектора через два данных неколлинеарных вектора):
Точки M и Q – середины сторон AB и AD параллелограмма ABCD. Выразите:
1) вектор через векторы 
и ;
2) вектор через векторы и 
;
3) вектор 
через векторы 
и 
;
4) вектор через векторы и .
4. Рассмотреть теорему о разложении вектора по двум данным неколлинеарным векторам, в ходе ее доказательства полезно обратить внимание на роль леммы в доказательстве.
IV. Закрепление изученного материала (решение задач).
1. Решить задачи № 000 (а, б); № 000 (б, в).
2. Решить задачи № 000 (по готовому чертежу) и № 000 (а, б).
Задание на дом: изучить материал пункта 86; решить задачи №№ 911 (в, г), 912 (ж, е, з), 916 (в, г).
Урок 2
Координаты вектора
Цели: ввести понятие координат вектора и рассмотреть правила действий над векторами с заданными координатами.
I. Проверка домашнего задания.
1. Устно решить задачи:
1) назвать числа х и у, удовлетворяющие равенству: 
; 
;
2. На доске двое учащихся решают задачи №№ 000 (в) и 912 (и, к).
II. Изучение нового материала.
1. Напомнить задание прямоугольной системы координат и начертить ее.
2. Ввести координатные векторы 
и 
(рис. 275).
3. Нулевой вектор можно представить в виде 
; его координаты равны нулю: 
(0; 0).
4. Координаты равных векторов соответственно равны.
5. Рассмотреть правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число (доказательства указанных правил учащиеся могут рассмотреть самостоятельно).
6. Записать в тетрадях правила:
и 
– данные векторы
1) 
;
2) 
;
3) 
.
III. Закрепление изученного материала (решение задач).
1. Решить задачу № 000 на доске и в тетрадях.
2. Устно по рисунку 276 решить задачу № 000.
3. Решить задачу № 000 (самостоятельно).
4. Решить задачу № 000 (а, в) на доске и в тетрадях.
5. Устно решить задачи № 000–925, используя правила, записанные в тетрадях.
6. Записать утверждение задачи № 000 без доказательства:
1) Если два вектора коллинеарны, то координаты одного вектора пропорциональны координатам другого: если 
коллинеарен вектору 
, то x1 : x2 = y1 : y2.
2) Если координаты одного вектора пропорциональны координатам другого вектора, то эти векторы коллинеарны.
7. Решить задачу № 000.
Используем условие коллинеарности векторов: 
.
1) 
(3; 7) и (6; 14), так как 
;
2) 
(–2; 1) и 
(2; –1), так как 
.
IV. Самостоятельная работа контролирующего характера.
Решить задачи № 000 (а, г); № 000 (г); № 000 (а, б); № 000 (а, в);
№ 000 (а).
Решить задачи №№ 000 (в, д); 920 (д); 988 (в, г); 921 (б, г); 914 (б).
Домашнее здание: подготовиться к устному опросу по карточкам, повторить материал пунктов 76–87; ответить на вопросы 1–20, с. 213–214 и на вопросы 1–8, с. 249 учебника; решить задачи №№ 000, 795; 990 (а) (для векторов 
и 
).
Урок 3
Связь между координатами вектора
и координатами его начала и конца.
Простейшие задачи в координатах
Цели: рассмотреть связь между координатами вектора и координатами его начала и конца; разобрать задачи о нахождении координат середины отрезка, о вычислении длины вектора по его координатам и нахождении расстояния между двумя точками.
1. Указать ошибки, сделанные учащимися при выполнении работы.
2. Решить на доске задачи, вызвавшие затруднения у учащихся.
II. Изучение нового материала (лекция).
1. Рассмотреть по учебнику рис. 277 и рис. 278 и ввести понятие радиус-вектора 
.
Без доказательства записать в тетрадях утверждения:
а) координаты точки М равны соответствующим координатам ее радиус-вектора;
б) каждая координата вектора равна разности соответствующих координат его конца и начала:
џ Устно решить задачу № 000.
2. Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.
3. Рассмотрим три вспомогательные задачи.
1) Координаты середины отрезка.
Используя формулу из п. 
и координаты векторов 
записать равенство в координатах: 
отсюда x = 
; y = 
.
Вывод: каждая координата середины отрезка равна полусумме соответствующих координат его концов.
џ Устно решить задачу № 000.
2) Вычисление длины вектора по его координатам.
Используя рис. 280 учебника, вывести формулу 
, если 
џ Устно решить задачу № 000.
3) Расстояние между двумя точками.
Пусть точка M1 (x1; y1) и точка M2 (x2; y2); тогда вектор 
(x2 – x1;
y2 – y1); следовательно, длина этого вектора может быть найдена по формуле 
но 
= d, таким образом, расстояние d между точками M1 (x1; y1) и M2 (x2; y2) выражается формулой
d = 
џ Решить задачу № 000 (а, б) на доске и в тетрадях.
III. Закрепление изученного материала (решение задач).
1. Решить задачу № 000.
Найти расстояние от точки М (3; –2): а) до оси абсцисс; точка В (x; y) лежит на оси абсцисс; тогда расстояние равно 2; б) расстояние до оси ординат равно 3; в) до начала координат равно d = 
2. Решить задачу № 000 на доске и в тетрадях.
MN = 
NP = 
MP = 
PΔMNP = 
.
Задание на дом: изучить материал пунктов 88, 89; решить задачи №№ 000, 952.
Урок 4
Простейшие задачи в координатах.
Решение задач
Цели: закрепить знания учащихся в ходе решения задач; учить решать задачи в координатах.
I. Повторение изученного материала.
1. Двое учащихся по карточкам работают у доски:
1) Вывести формулы координат середины отрезка.
2) Решить задачу № 000.
1) Вывести формулу расстояния между двумя точками.
2) Решить задачу № 000.
2. С остальными учащимися проводится устная работа по решению задач:
1) Найдите координаты вектора , равного разности векторов 
и 
, если (–5; 6), (0; –4).
2) Найдите координаты вектора , равного сумме векторов и , если (3; 7), (4; –5).
3) Найдите координаты середины отрезка DK, если D (–6; 4), K (2; –8).
4) Найдите длину отрезка CP, если С (3; –2), P (–5; 4).
5) Найдите длину вектора , равного 
, если 
(5; 0) и (0; –12).
6) Найдите координаты вектора 3, если (4; –2); вектора –2, если (–2; 5).
II. Решение задач.
1. Решить задачу № 000 (а).
Найдем длины сторон треугольника АВС по формуле
d = 
:
AB = 
BC = 
AC = 
Так как АВ = АС, то по определению равнобедренного треугольника АВС – равнобедренный. Найдем его площадь; проведем высоту АМ 
ВС:
SΔABC = BC ∙ AM; AM – высота и медиана в равнобедренном треугольнике.
x = 
= 3; y = 
= –1.
Значит, точка М (3; –1).
Найдем длину отрезка AM = 
Площадь треугольника АВС равна S = 
= 13.
2. Решить задачу № 000 (б).
d = ; (2x + 1)2 + (3 – x)2 = 72;
3. Решить задачу № 000 (б) на доске и в тетрадях.
Пусть точка М (0; y) лежит на оси ординат; по условию МС = MD;
(4 – 0)2 + (–3 – y)2 = (8 – 0)2 + (1 – y)2;
Значит, точка М (0; 5).
4. Решить задачу № 000 (б) на доске и в тетрадях.
Найдем координаты точки пересечения диагоналей четырехугольника О (x; y): для диагонали NQ имеем:
x = 
= –3;
y = 
= 3; точка О (–3; 3).
Для диагонали МР имеем:
x = 
= –3; y = 
= 3; точка О (–3; 3).
Значит, диагонали MP и NQ точкой пересечения делятся пополам; по признаку параллелограмма MNPQ – параллелограмм.
MP = 
NQ = 
Ответ: 4 
и 2.
5. Решить задачу № 000 (а).
AB =
= 4;
CD =
= 4;
BC =
= 2;
AD =
=2.
Так как AB = CD = 4 и BC = AD = 2, то по II признаку параллелограмма ABCD – параллелограмм. Найдем диагонали АС и BD параллелограмма ABCD: AC =
BD =
Если диагонали равны AC = BD, то ABCD – прямоугольник.
III. Итоги урока.
Домашнее здание: повторить материал пунктов 88 и 89; решить задачи №№ 000 (б), 949 (а), 951 (б), 953.
Урок 5
Уравнение линии на плоскости.
Уравнение окружности
Цели: познакомить учащихся с понятием уравнения линии на плоскости; вывести уравнение окружности и научить записывать уравнение окружности.
I. Математический диктант (10–15 мин).
1. Найдите координаты середины отрезка AB, если A (–2; 3), B (6; –3).
2. Найдите длину отрезка EH, если E (–3; 8), H (2; –4).
3. Какая фигура состоит из множества всех точек плоскости, каждая из которых равноудалена от двух данных точек?
4. Принадлежит ли точка A (–6; 2) графику функции y = – 0,5x?
5. Функция задана уравнением y = 2x – 3. Какая линия служит графиком этой функции?
6. На окружности радиуса 7 см даны точки А и В, расстояние между которыми равно 13 см. лежит ли центр окружности на прямой АВ?
7. Вершины треугольника ABC имеют следующие координаты: А (8; –3); В (5; 1); С (12; 0). Докажите, что 
B = C.
1. Найдите координаты середины отрезка CD, если C (3; –4), D (–3; 6).
2. Найдите длину отрезка KB, если K (–6; –3), B (2; 3).
3. Прямая l является серединным перпендикуляром к основанию AB треугольника ABC и проходит через вершину C. Определите вид треугольника ABC.
4. Принадлежит ли точка В (2; –8) графику функции y = – 4x?
5. Функция задана уравнением y = 5 – x. Какая линия служит графиком этой функции?
6. Какой фигурой является множество точек, равноудаленных от данной точки?
7. Вершины четырехугольника ABCD имеют следующие координаты: А (–3; –1); В (1; 2); С (5; –1), D (1; –4). Докажите, что этот четырехугольник – ромб.
II. Объяснение нового материала.
1. Разобрать пятое задание диктанта, обратив внимание учащихся на то, что им уже известны графики некоторых функций. В частности, графиком линейной функции y = kx + b является прямая линия, а уравнение y = kx + b называется уравнением этой прямой.
2. Вспомнить уравнения параболы и гиперболы и их графики.
3. Понятие уравнения произвольной линии дается в ознакомитель-ном плане. При этом важно добиться понимания учащимися следующего: чтобы установить, что данное уравнение является уравнением данной линии, нужно доказать, что: 1) координаты любой точки линии удовлетворяют данному уравнению и 2) координаты любой точки, не лежащей на данной линии, не удовлетворяют этому уравнению.
4. Введение уравнения окружности радиуса r с центром С в заданной прямоугольной системе координат (рис. 286):
где C (x0; y0). Уравнение окружности радиуса r с центром в начале координат О (0; 0) имеет вид: x2 + y2 = r2.
5. Не любое уравнение второй степени с двумя переменными задает окружность. Например, уравнение 4х2 + у2 = 4 в прямоугольной системе координат не окружность, а эллипс (с этой фигурой учащиеся знакомились в курсе черчения), уравнение х2 + у2 = 0 задает единственную точку – начало координат, а уравнению х2 + у2 = –4 не удовлетворяют координаты ни одной точки, поэтому это уравнение не задает никакой фигуры.
Видео:Пятнадцатое задание ОГЭ по математике(12) #огэ #огэ2023 #огэпоматематике #математика #огэматематикаСкачать
Точки m и n середины сторон bc и ad четырехугольника abcd точки p и k
БАЗА ЗАДАНИЙ
Задание № 16. Планиметрия с доказательством.
1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.
2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3
3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3
4. В треугольнике ABC точки A 1 , B 1 , C 1 — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A1, B1, C1, H— лежат на одной окружности.
б) Найдите A1 H, если BC = 2√3.
5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10
6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4
7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6
8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.
9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.
10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.
11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88
12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.
13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C 1 , B 1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB 1 C 1 .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B 1 C 1 =6 и площадь треугольника AB 1 C 1 в восемь раз меньше площади четырёхугольника BCB 1 C 1 .
15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.
16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.
17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65
18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4
19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .
б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2
20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3
21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1
22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36
23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4
24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.
25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.
26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.
27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.
28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
🎥 Видео
№68. Точки М и N — середины ребер АВ и АС тетраэдра ABCD. Докажите, что прямая MN параллельнаСкачать
ОГЭ. Геометрия. Из открытого банка заданий ОГЭ (ФИПИ). Медианы №1Скачать
Геометрия Точки M, K, N, P являются соответственно серединами сторон AB, BC, CD и AD квадрата ABCDСкачать
Геометрия Точки M и K – середины сторон AB и AC треугольника ABC соответственно. Найдите периметрСкачать
№346. Точки М и N — середины оснований АВ и CD трапеции ABCD, а О — произвольнаяСкачать
№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать
1707 точка M и N являются серединами сторон AB и BC треугольника ABCСкачать
№166. Отрезки АВ и CD пересекаются в их общей середине О. Точки М и N — середины отрезков АС и BD.Скачать
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Красивая задача №3 из ЕГЭ-2022. Параллелограмм Вариньона |ЕГЭ по математике профильного уровняСкачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
№ 401-500 - Геометрия 9 класс МерзлякСкачать
№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать
№555. Точки М, N и Р лежат соответственно на сторонах АВ, ВС и СА треугольника ABC, причем MN||AC,Скачать
