Точки авсд середины ребер прямоугольного параллелепипеда назовите параллельные прямые

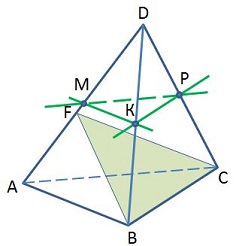
Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB.

Комментарий:
1) МК – средняя линия треугольника ADB, следовательно МК || АВ.
2) АВ лежит в плоскости FАB, следовательно по признаку параллельности прямой и плоскости МК || FАВ

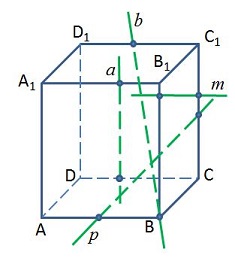
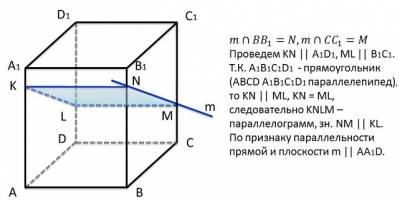
АВСDA ₁ B₁ C₁ D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁ AD?

Комментарий:

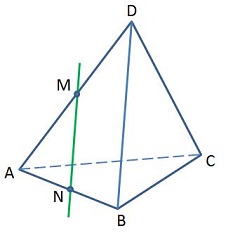
В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN?

Комментарий:
MN – средняяя линия треугольника ADB, значит MN || DB. По признаку параллельности прямой и плоскости MN || DBC.

Выберите ВЕРНЫЕ высказывания:

1Параллельные прямые не имеют общих точек.2Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.3Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.4Существует параллелепипед, у которого все углы граней острые

Комментарий
«Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.»
Высказывание № 1 – верно. «не пересекаются», значит не имеют общих точек
Высказывание № 2 – неверно. не каждая прямая, лежащая в параллельной для данной прямой плоскости, так же будет лежать в одной плоскости с этой прямой.
Высказывание № 3 – верно. Линия пересечения плоскостей – это прямая, принадлежащая каждой из этих плоскостей, следовательно данная прямая параллельна данным плоскостям по признаку параллельности прямой и плоскости.
Высказывание № 4 – не верно. грани параллелепипеда – параллелограммы, противоположные стороны каждого из которых параллельны, следовательно углы при них и секущей (смежная сторона) в сумме равны 180 0
Если все углы граней будут острыми, то сумма одностосронних углов будет меньше 180 0 . Получили противоречие.

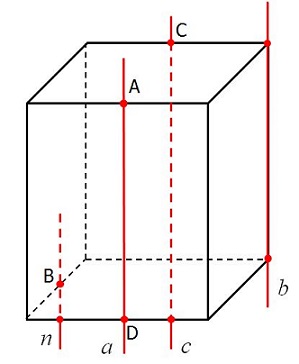
Точки А, В, С и D – середины ребер прямоугольного параллелепипеда. Назовите параллельные прямые.

1a || n2a || b3b || c4a || c

Комментарий
a || b, т.к. каждая из этих прямых параллельна одному и тому же ребру параллелепипеда – линии пересечения плоскостей, в которых лежат данные прямые.

Тестовые задания по геометрии к разделу «Прямые и плоскости в пространстве» 1 курс СПО

Тестовые задания по геометрии к разделу «Прямые и плоскости в пространстве»1.Аксиомы стереометрии. 2.Параллельность прямых и плоскостей. 3.Перпендикулярность прямых и плоскостей. Ответы в конце разработки

Просмотр содержимого документа
«Тестовые задания по геометрии к разделу «Прямые и плоскости в пространстве» 1 курс СПО»

Прямые и плоскости в пространстве

Предмет стереометрии. Основные понятия и аксиомы стереометрии.

Параллельность прямыхв пространстве. Параллельность двух плоскостей.

Векторы в пространстве.

Перпендикулярность прямых, прямой и плоскости.

Перпендикуляр и наклонная.

Угол между прямой и плоскостью.

Двугранный угол. Перпендикулярность плоскостей.

Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.

1) АВС 2) DBC 3) DAB 4) DAC

Каким плоскостям принадлежит точка К?

Выберите верные высказывания:

1) Любые три точки лежат в одной плоскости.

2) Если центр окружности и ее точка лежат в плоскости, то и вся окружность лежит в этой плоскости.

3) Через три точки, лежащих на прямой, проходит только одна плоскость.

4) Через две пересекающихся прямые проходит плоскость , и притом только одна.

Выберите неверные высказывания:

1) Если три прямые имеют общую точку, то они лежат в одной плоскости.

2) Прямая, пересекающая две стороны треугольника, лежит в плоскости этого треугольника.

3) Две плоскости могут имеет только две общие точки.

4) Три попарно пересекающиеся в разных точках прямые, лежат в одной плоскости.

Назовите прямую, по которой пересекаются плоскости A₁BC и A₁AD.

Назовите прямую, по которой пересекаются плоскости DCC₁ и A₁AD.

Прямые АВ и CD пересекаются. Через прямую АВ проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью ВСD.

1) АС 2) АB 3) BС 4) ВD

Прямые АВ и CD пересекаются. Через точки В и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AСD.

1) АС 2) АB 3) BС 4) ВD

Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.

1) АВС 2) DBC 3) DAB 4) DAC

Каким плоскостям принадлежит точка F?

Выберите верные высказывания:

1) Любые четыре точки лежат в одной плоскости.

2) Через прямую и не лежащую на ней точку проходит только одна плоскость.

3) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости .

4) Две плоскости могут иметь только одну общую точку.

Выберите неверные высказывания:

1) Две окружности, имеющие общий центр, лежат в одной плоскости .

2) Прямая, проходящая через вершину треугольника, лежит в плоскости этого треугольника.

3) Три вершины треугольника принадлежат одной плоскости.

4) Через две параллельные прямые проходит плоскость , и притом только одна.

Назовите прямую, по которой пересекаются плоскости DCC₁ и A₁BC.

Назовите прямую, по которой пересекаются плоскости ABC и C₁CB.

Прямые АВ и CD пересекаются. Через прямую CD проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AВС.

1) СD 2) АD 3) BС 4) ВD

Прямые АВ и CD пересекаются. Через точки A и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью BСD.

1) АС 2) АD 3) BС 4) ВD

Параллельность прямых и плоскостей

Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FBC.

1) МР 2) РК 3) МК 4) МК и РК

АВСDA₁B₁C₁D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁B₁C₁?

В тетраэдре DАВС ВК = КС, DP = PC. Плоскости какой грани параллельна прямая РК?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.

3) Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.

4) Скрещивающиеся прямые не имеют общих точек.

Точки А, В, С и D – середины ребер прямоугольного

параллелепипеда. Назовите параллельные прямые.

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:

1) Прямые СD и MN скрещивающиеся.

2) Прямые АВ и MN лежат в одной плоскости.

3) Прямые СD и MN пересекаются.

4) Прямые АВ и СD скрещивающиеся.

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Треугольники АВК и АВF расположены так, что прямые АВ и FK скрещиваются. Как расположены прямые АК и ВF?

1) они параллельны 2) скрещиваются 3) пересекаются

В тетраэдре DАВС АВ = ВС = АС = 20; DA = DB = DC = 40. Через середину ребра АС плоскость, параллельная АD и ВC. Найдите периметр сечения.

Параллельность прямых и плоскостей

Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB.

1) МР 2) РК 3) МК 4) МК и РК

АВСDA₁B₁C₁D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁AD?

В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Параллельные прямые не имеют общих точек.

2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.

4) Существует параллелепипед, у которого все углы граней острые.

Точки А, В, С и D – середины ребер прямоугольного

параллелепипеда. Назовите параллельные прямые.

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:

1) Прямые СD и MN пересекаются.

2) Прямые АВ и MN скрещивающиеся

3) Прямые АВ и СD параллельные.

4) Прямые АВ и MN пересекаются

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Два равнобедренных треугольника АВС и АВD с общим основанием АВ расположены так, что точка С не лежит в плоскости АВD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам ВС и ВD.

1) они параллельны 2) скрещиваются 3) пересекаются

В тетраэдре DАВС АВ = ВС = АС = 10; DA = DB = DC = 20. Через середину ребра ВС плоскость, параллельная АС и ВD. Найдите периметр сечения.

Перпендикулярность прямых и плоскостей

Через сторону АВ треугольника АВС проведена плоскость, перпендикулярная к стороне ВС. Определите вид треугольника относительно углов.

1) остроугольный 2) прямоугольный 3) тупоугольный

Треугольник АВС – правильный, О – центр треугольника. Расстояние от точки М до вершины А равно 3. Найдите высоту треугольника.

АВСD – параллелограмм; Найдите периметр параллелограмма.

1) 20 2) 25 3) 40 4) 60

Через вершину А треугольника ABC проведена плос­кость α, параллельная ВС. Расстояние от ВС до плоскости α равно 12. Найдите расстояние от точки пересечения ме­диан треугольника АВС до этой плоскости.

1) 8 2) 6 3) 12 4) 18

Высота ромба равна 12. Точка М равноудалена от всех сторон ромба и находится на расстоянии, равном 8, от его плоскости. Чему равно расстояние точки М до сторон ромба?

На рисунке Найдите угол между МС и плоскостью АМВ.

1) 30 0 2) 60 0 3) 90 0 4) 45 0

Выберите верные высказывания:

1) Прямая пересекает параллельные плоскости под разными углами.

2) Две прямые, перпендикулярные к одной плоскости, параллельны.

3) Длина перпендикуляра меньше длины наклонной, проведенной из той же точки.

4) Две скрещивающиеся прямые могут быть перпендикулярными к одной плоскости.

Отрезок АВ упирается концами А и В в грани прямого двугранного угла. Расстояния от точек А и В до ребра равны 1, а длина отрезка АВ равна 3. Найдите длину про­екции этого отрезка на ребро.

В тетраэдре DABC АО пресекает ВС в точке Е; Найдите .

Прямоугольник ABCD и параллелограмм ВЕМС распо­ложены так, что их плоскости взаимно перпендикулярны. Найдите угол MCD.

1) 90 0 2) 60 0 3) 30 0 4) 45 0

Перпендикулярность прямых и плоскостей

Через сторону АD параллелограмма АВСD, проведена плоскость, перпендикулярная к стороне DС. Определите вид треугольника АВС.

1) остроугольный 2) прямоугольный 3) тупоугольный

Треугольник АВС – правильный, О – центр треугольника. Высота треугольника равна 3. Найдите расстояние от точки М до вершин треугольника.

АВСD – параллелограмм; Найдите BD.

1) 20 2) 15 3) 40 4) 10

Через вершину А треугольника ABC проведена плос­кость α, параллельная ВС. Расстояние от точки пересече­ния медиан треугольника АВС до этой плоскости равно 4. На каком расстоянии от плоскости находится ВС?

1) 8 2) 6 3) 12 4) 14

Точка Р удалена от всех сторон ромба на расстояние» равное , и находится от его плоскости на расстоянии равном 2. Чему равна сторона ромба, если его угол 30°?

На рисунке Найдите угол между МС и плоскостью АМВ.

1) 30 0 2) 60 0 3) 90 0 4) 45 0

Выберите верные высказывания:

1) Угол между прямой и плоскостью может быть не больше 90 0 .

2) Две плоскости, перпендикулярные к одной прямой, пересекаются.

3) Длина перпендикуляра больше длины наклонной, проведенной из той же точки.

4) Диагональ прямоугольного параллелепипеда больше любого из ребер.

Отрезок АВ упирается концами А и В в грани прямого двугранного угла. Расстояния от точек А и В до ребра равны 2, а длина отрезка АВ равна 4. Найдите длину про­екции этого отрезка на ребро.

В тетраэдре DABC основание ABC — правильный тре­угольник. Вершина D проецируется в его центр О. Найди­те угол между плоскостью ADO и гранью DCB.

1) 30 0 2) 60 0 3) 90 0 4) 45 0

Треугольник АМВ и прямоугольник ABCD расположе­ны так, что их плоскости взаимно перпендикулярны. Най­дите угол MAD.

Тест 2 Параллельность прямых и плоскостей

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Параллельность прямых и плоскостей

Точки М, Р, К – середины ребер DA , DB , DC тетраэдра DABC . Назовите прямую, параллельную плоскости FBC .

1) МР 2) РК 3) МК 4) МК и РК

АВС DA ₁ B ₁ C ₁ D ₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A ₁ B ₁ C ₁ ?

В тетраэдре D АВС ВК = КС, DP = PC . Плоскости какой грани параллельна прямая РК?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.

3) Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.

4) Скрещивающиеся прямые не имеют общих точек.

Точки А, В, С и D – середины ребер прямоугольного

параллелепипеда. Назовите параллельные прямые.

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:

1) Прямые С D и MN скрещивающиеся.

2) Прямые АВ и MN лежат в одной плоскости.

3) Прямые С D и MN пересекаются.

4) Прямые АВ и С D скрещивающиеся.

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Треугольники АВК и АВ F расположены так, что прямые АВ и FK скрещиваются. Как расположены прямые АК и В F ?

1) они параллельны 2) скрещиваются 3) пересекаются

В тетраэдре D АВС АВ = ВС = АС = 20; DA = DB = DC = 40. Через середину ребра АС плоскость, параллельная А D и В C . Найдите периметр сечения.

Параллельность прямых и плоскостей

Точки М, Р, К – середины ребер DA , DB , DC тетраэдра DABC . Назовите прямую, параллельную плоскости F А B .

1) МР 2) РК 3) МК 4) МК и РК

АВС DA ₁ B ₁ C ₁ D ₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A ₁ AD ?

В тетраэдре D АВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN ?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Параллельные прямые не имеют общих точек.

2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.

4) Существует параллелепипед, у которого все углы граней острые.

Точки А, В, С и D – середины ребер прямоугольного

параллелепипеда. Назовите параллельные прямые.

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания:

1) Прямые С D и MN пересекаются.

2) Прямые АВ и MN скрещивающиеся

3) Прямые АВ и С D параллельные.

4) Прямые АВ и MN пересекаются

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

Два равнобедренных треугольника АВС и АВ D с общим основанием АВ расположены так, что точка С не лежит в плоскости АВ D . Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам ВС и В D .

1) они параллельны 2) скрещиваются 3) пересекаются

В тетраэдре D АВС АВ = ВС = АС = 10; DA = DB = DC = 20. Через середину ребра ВС плоскость, параллельная АС и В D . Найдите периметр сечения.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 964 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Чимчарова Патимат АбдулаевнаНаписать 7079 01.10.2019

Номер материала: ДБ-717022

26.09.2019 130

25.09.2019 67

22.09.2019 281

22.09.2019 155

22.09.2019 312

22.09.2019 860

18.09.2019 769

03.09.2019 170

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📸 Видео