Как найти точку касания прямой и окружности в параметрах (4 видео)

Задание 6. Касательная и уравнение с параметром

Самыми сложными задачами 6 считаются задачи с параметром. Сегодня мы разберем одну из таких задач — это еще относительно простой пример, на котором, однако, довольно удобно тренироваться.

Задача B9. Прямая y = 10 x − 30 является касательной к графику функции:

y = 2 x 2 + bx + 2

Найдите значение параметра b , если известно, что абсцисса точки касания положительна.

Следующий видеоурок — последний в этой короткой серии — будет посвящен самой сложной задаче B9 из всех, которые могут встретиться на реальном ЕГЭ по математике. Разумеется, при желании можно придумать еще более сложные задачи. Но на настоящем экзамене более сложных уже не будет.

Содержание

Задачи с параметрами. Условия касания.
Касательная к окружности
Свойство касательной
Теорема, обратная теореме о свойстве касательной
Построение касательной к окружности
🎥 Видео

Видео:Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать

Задачи с параметрами. Условия касания.

Темы для повторения:

Графический метод решения задач с параметрами

Друзья, мы продолжаем тему «Задачи с параметрами». Это №18 Профильного ЕГЭ по математике. В этой статье рассказано, как в решении задач с параметрами применяется производная.

Рассмотрим следующую задачу:

При каких значениях параметра a уравнение имеет ровно 2 решения?

Поскольку логарифмы определены для положительных чисел, Это значит, что

Сделаем замену При каждому значению соответствует два значения

В левой части уравнения — линейная функция, в правой — логарифмическая. Это функции разных типов. Пытаться справиться с таким уравнение аналитически — бесполезно. Попробуем графический способ.

Если , то и условие не выполняется. Рассмотрим по отдельности случаи и

Пусть . Нарисуем графики функций и Функция монотонно возрастает при . Обозначим Функция монотонно убывает при .

Докажем, что графики функций и имеют единственную точку пересечения при и любом

Рассмотрим функцию Функция является монотонно возрастающей при (как сумма монотонно возрастающих функций и ), следовательно, каждое свое значение, в том числе и значение , она принимает ровно один раз.

Уравнение имеет единственное решение при положительных и Значит, при всех исходное уравнение имеет ровно 2 решения. Теперь случай

Уравнение имеет единственное решение, если прямая касается графика функции Мы помним, как записываются условия касания:

В нашем случае

Учитывая, что , получим:

Мы получили, что, — точка касания. При этом .

Ответ:

Видео:Параметр. Серия 12. Решение задач с окружностями. Касание окружности и прямойСкачать

Касательная к окружности

Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

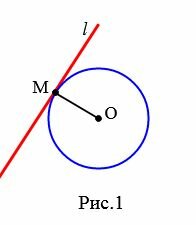
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.

Как найти точку касания прямой и окружности в параметрах

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Свойство касательной

Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.

Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)

Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.

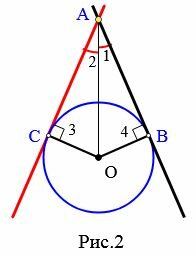
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.

Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.

Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Теорема, обратная теореме о свойстве касательной

Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.

Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).

Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Построение касательной к окружности

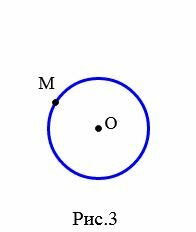
Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).

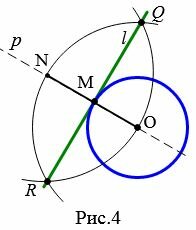Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.

Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).

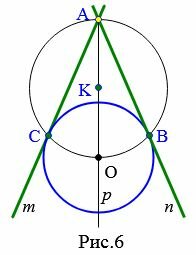Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.