Точки abcd не лежат на одной прямой являются параллельными проекциями трех последовательных вершин

Контрольная работа # 2 по геометрии в 10 классе (базовый уровень) «Параллельность в пространстве» для УМК Мерзляк, Номировский, Поляков, под ред. В. Е. Подольского в 4-х вариантов. Геометрия 10 Контрольная 2 Мерзляк. Ответов нет.

Геометрия 10 класс (УМК Мерзляк)
Контрольная работа № 2

Параллельность в пространстве

Вариант 1

1. Точки M, N, P и Q — середины отрезков BC, BD, AD и AC соответственно, AB = 14 см, CD = 18 см (рис. 9). Определите вид четырёхугольника MNPQ и вычислите его периметр.
2. Плоскость а пересекает стороны AB и BC треугольника ABC в точках M и K соответственно и параллельна стороне AC, MK = 4 см, MB : MА = 2 : 3. Найдите сторону AC треугольника.
3. Треугольник ABC является изображением правильного треугольника A₁B₁C₁ (рис. 10). Постройте изображение высоты треугольника, опущенной на сторону AC₁.
4. Плоскости а и b параллельны. Из точки M, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости a и b в точках А₁ и B₁, а другой — в точках А₂ и B₂ соответственно. Найдите отрезок В₁В₂, если он на 2 см больше отрезка А₁А₂, МВ₁ = 7 см, А₁B₁ = 4 см.
5. Точки A, B, C, не лежащие на одной прямой, являются параллельными проекциями трёх последовательных вершин правильного шестиугольника. Постройте изображение этого шестиугольника.

Вариант 2

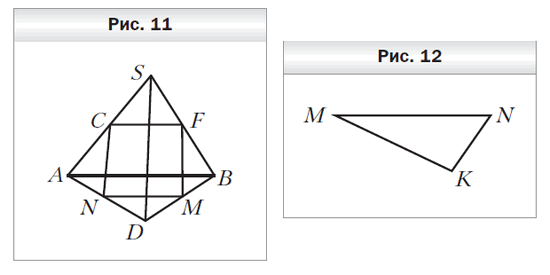
1. Точки F, M, N и C — середины отрезков BS, DB, AD и AS соответственно, SD = 30 см, AB = 36 см (рис. 11). Определите вид четырёхугольника FMNC и вычислите его периметр.
2. Плоскость b пересекает стороны AB и AC треугольника ABC в точках N и D соответственно и параллельна стороне BC, AD = 6 см, DN : CB = 3 : 4. Найдите сторону AC треугольника.
3. Треугольник MNK является изображением правильного треугольника M₁N₁K₁ (рис. 12). Постройте изображение биссектрисы треугольника, проведённой из вершины M₁.
4. Плоскости а и b параллельны. Через точку M, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости а и b в точках А₁ и B₁, а другая — в точках А₂ и B₂ соответственно. Найдите отрезок А₁А₂, если он на 1 см меньше отрезка B₁B₂, MA₂ = 4 см, А₂B₂ = 10 см.
5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин квадрата и его центра. Постройте изображение квадрата.

Вариант 3

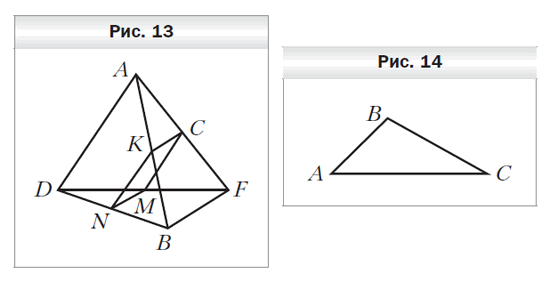
1. Точки N, M, C и K — середины отрезков BD, DF, FA и AB соответственно, BF = 24 см, AD = 18 см (рис. 13). Определите вид четырёхугольника NMCK и вычислите его периметр.
2. Плоскость а пересекает стороны MF и MK треугольника MFK в точках A и B соответственно и параллельна стороне FK, AB = 12 см, AM : AF = 3 : 5. Найдите сторону FK треугольника.
3. Треугольник ABC является изображением правильного треугольника А₁B₁C₁ (рис. 14). Постройте изображение центра вписанной окружности треугольника А₁B₁C₁.
4. Плоскости а и b параллельны. Из точки O, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости а и b в точках C₁ и D₁, а другой — в точках C₂ и D₂ соответственно. Найдите отрезок C₁C₂, если он на 5 см меньше отрезка D₁D₂, OC₁ = 4 см, C₁D₁ = 10 см.
5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин правильного треугольника и его центра. Постройте изображение этого треугольника.

Вариант 4

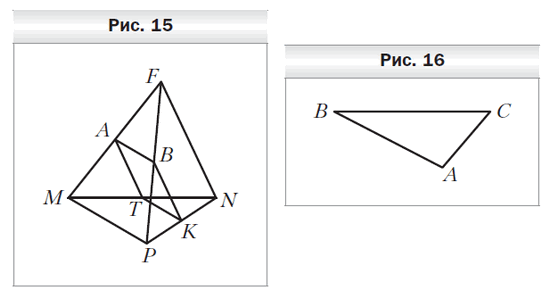
1. Точки A, B, K и T — середины отрезков MF, PF, PN и MN соответственно, MP = 10 см, FN = 16 см (рис. 9). Определите вид четырёхугольника ABKT и вычислите его периметр.
2. Плоскость b пересекает стороны CF и CD треугольника CDF в точках M и N соответственно и параллельна стороне FD, MN = 6 см, FD = 21 см, MC = 10 см. Найдите сторону FC треугольника.
3. Треугольник ABC является изображением правильного треугольника А₁B₁C₁ (рис. 16). Постройте изображение центра описанной окружности треугольника А₁B₁C₁.
4. Плоскости а и b параллельны. Через точку D, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости а и b в точках M₁ и N₁, а другая — в точках M₂ и N₂ соответственно. Найдите отрезок M₁M₂, если он на 8 см больше отрезка N₁N₂, N₁M₁ = 30 см, DN₁ = 5 см.
5. Точки A, B и M, не лежащие на одной прямой, являются соответственно параллельными проекциями двух соседних вершин параллелограмма и середины его противолежащей стороны. Постройте изображение этого параллелограмма.

Вы смотрели: Контрольная работа по геометрии в 10 классе (базовый уровень) «Параллельность в пространстве» для УМК Мерзляк, Номировский, Поляков, под ред. В. Е. Подольского в 4-х вариантов. Геометрия 10 Контрольная 2 Мерзляк. Ответов нет.

(с) Цитаты из пособия «Математика : алгебра и начала математического анализа, геометрия. Геометрия. Базовый уровень : 10 класс : методическое пособие / Е. В. Буцко, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. — М.: Вентана-Граф» использованы в учебных целях.

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:№12. Точки А, В, С, D не лежат в одной плоскости. Пересекаются ли плоскости, проходящие через точкиСкачать

Точки abcd не лежат на одной прямой являются параллельными проекциями трех последовательных вершин

§ 12. Параллельное проектирование и его свойства.

В начале учебника на плоскости изображены некоторые фигуры, расположенные в пространстве. Эти изображения строились с целью придать наглядность тому, о чём шла речь в соответствующей теореме или задаче.

Однако изображения пространственных фигур на плоскости строятся по определённым правилам и в школьном курсе геометрии обычно осуществляются с помощью метода параллельного проектирования, сущность которого состоит в следующем.

В пространстве выбирается произвольная плоскость π Плоскость проекций в начертательной геометрии чаще всего обозначают π . , которую называют плоскостью проекций или плоскостью изображения , и прямая l , пересекающая эту плоскость (рис. 71, а ).

Пусть M ′ — произвольная точка пространства. Через эту точку проведём прямую p , параллельную l . Точка M пересечения прямой p с плоскостью π называется параллельной проекцией точки M ′ на плоскость π в направлении прямой l . Если M ′ — точка плоскости π , то M совпадает с M ′ .

При этом часто пользуются обозначением: M = П ( M ′ ).

Прямую l и все прямые пространства, параллельные ей, называют проектирующими прямыми ; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью .

Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, её определяющих. На рисунке 71, б треугольник ABC является параллельной проекцией треугольника A ′ B ′ C ′ на плоскость π в направлении прямой l .

Замечание. Наряду с параллельным проектированием рассматривается также центральное проектирование фигур на плоскость. В этом случае проектирующие прямые проходят через одну точку — центр проектирования , произвольно выбранную вне плоскости проекций (рис. 71, в ).

Параллельное и центральное проектирование можно наблюдать в реальном пространстве: тень, которую отбрасывает предмет в солнечный день, является параллельной проекцией этого предмета, так как солнечные лучи можно считать приближённо параллельными вследствие большого удаления Солнца от Земли. А изображение на экране кинотеатра фигуры, заснятой на киноплёнку, является центральной проекцией этой фигуры.

На рисунках 72, 73, 74 изображены в параллельной проекции соответственно квадрат, треугольник и каркас тетраэдра. По этим рисункам можно сделать предположение, что ни величина угла, ни длина отрезка при параллельном проектировании, вообще говоря, не сохраняются.

Рассмотрим некоторые свойства параллельного проектирования.

1. Все точки проектирующей прямой проектируются в одну точку — точку пересечения этой прямой с плоскостью проекций (рис. 75).

В дальнейшем мы будем рассматривать проекции прямых, не параллельных проектирующим прямым.

2. Проекция прямой есть прямая. Действительно, все прямые, проектирующие точки данной прямой m ′ (рис. 76), принадлежат некоторой проектирующей плоскости, которая пересекает плоскость проекций по некоторой прямой m — параллельной проекции прямой m ′ .

Причём, так как через точку, не лежащую на данной прямой, можно провести лишь одну прямую, параллельную этой прямой (т. 6) (мы проводим прямые, параллельные прямой l ), то каждая точка прямой m ′ проектируется в единственную точку своей проекции — прямой m , и наоборот, каждая точка прямой m является проекцией единственной точки прямой m ′ .

Из доказательства этого свойства следует: три точки, лежащие на одной прямой, проектируются в три точки, также лежащие на одной прямой .

Также говорят, что три коллинеарные точки проектируются в три коллинеарные точки .

3. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Действительно, если прямые a ′ и b ′ лежат в одной проектирующей плоскости, то они проектируются в одну и ту же прямую, а именно, в прямую, по которой эта проектирующая плоскость пересекает плоскость проекций.

Пусть теперь прямые a ′ и b ′ параллельны (рис. 77) и не лежат в одной проектирующей плоскости.

Обозначим через α и β плоскости, образованные прямыми, проектирующими точки прямых соответственно a ′ и b ′ . Прямые a и b , по которым плоскости α и β пересекают плоскость проекции, не могут пересекаться, так как если бы эти прямые имели общую точку M , то и прямые a ′ и b ′ по свойству 2 имели бы общую точку M ′ , что невозможно в силу параллельности прямых a ′ и b ′ . А так как прямые a и b лежат в одной плоскости (плоскости проекций) и не имеют общей точки, то они параллельны, т. е. параллельными проекциями параллельных прямых, не лежащих в одной проектирующей плоскости, являются параллельные прямые.

Заметим, что плоскости α и β , проектирующие параллельные прямые a ′ и b ′ , не лежащие в одной проектирующей плоскости, параллельны (в п. 9.1 показано, что параллельные плоскости существуют; о свойствах параллельных плоскостей речь пойдёт в следующей главе).

4. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков.

Если отрезки A ′ B ′ и B ′ C ′ лежат на одной прямой a ′ и проектируются на отрезки соответственно AB и BC прямой a (рис. 78), то по обобщённой теореме Фалеса в плоскости, определяемой прямыми a и a ′ , получаем A ′ B ′ : B ′ C ′ = AB : BC = m : n .

Пусть теперь отрезки A ′ B ′ и C ′ D ′ расположены соответственно на данных параллельных прямых a ′ и b ′ , не лежащих в одной проектирующей плоскости, и A ′ B ′ : C ′ D ′ = m : n ; AB и CD , a и b — соответственно их параллельные проекции на плоскость π (рис. 79).

Так как a ′ ‖ b ′ , то (по свойству 3) a ‖ b . Пусть E — такая точка прямой a , что четырёхугольник BCDE — параллелограмм. Тогда на прямой a ′ существует (единственная!) такая точка E ′ , что E ′ E ‖ DD ′ и A ′ B ′ : B ′ E ′ = AB : BE . А так как BC ‖ ED , то B ′ C ′ ‖ E ′ D ′ (по свойству 3), значит, B ′ C ′ D ′ E ′ — параллелограмм. Поэтому A ′ B ′ : C ′ D ′ = A ′ B ′ : B ′ E ′ = AB : BE = AB : CD , т. е. A ′ B ′ : C ′ D ′ = AB : CD = m : n .

Из этого свойства, очень важного для теории построений изображений пространственных фигур на плоскости, следует не менее важный вывод: если отрезок A ′ C ′ параллельно проектируется на отрезок AC и точка B ′ делит отрезок A ′ C ′ в отношении A ′ B ′ : B ′ C ′ = m : n , то точка B — проекция точки B ′ — делит отрезок AC в том же отношении m : n , т. е. AB : BC = A ′ B ′ : B ′ C ′ = m : n . В частности, середина отрезка A ′ C ′ параллельно проектируется в середину отрезка AC ( m : n = 1 : 1) (рис. 80).

Пусть M — внутренняя точка отрезка AB .

Определение. Число λ , равное отношению длин отрезков AM и MB , на которые точка M делит отрезок AB , называется простым отношением трёх точек A , B и M , лежащих на одной прямой, и обозначается ( AB ; M ), т. е. ( AB ; M ) = λ = AM : MB .

При этом точки A и B называются базисными , а точка M — делящей точкой.

Упорядоченность точек простого отношения необходима. Например, если AA 1 — медиана треугольника ABC , M — его центроид (точка пересечения медиан треугольника), то ( AA 1 ; M ) = AM : MA 1 = 2 : 1, но ( A 1 A ; M ) = A 1 M : MA = 1 : 2 (рис. 81). Поэтому, если AM ≠ MA 1 , то

( AA 1 ; M ) ≠ ( A 1 A ; M ).

Учитывая свойство 4 параллельного проектирования, можно сделать вывод: простое отношение трёх точек, лежащих на одной прямой, при параллельном проектировании сохраняется . В этом случае также говорят, что простое отношение трёх точек, лежащих на одной прямой, — инвариант параллельного проектирования .

Свойства фигуры, сохраняющиеся при параллельном проектировании, называются аффинными свойствами этой фигуры. Например, свойства прямых быть параллельными — аффинное свойство этих прямых; инвариантность простого отношения трёх точек одной прямой — аффинное свойство таких точек.

Подробнее о параллельном проектировании и изображениях фигур на плоскости читайте в конце учебника.

Определение. Проектирование в направлении прямой, перпендикулярной плоскости проекций, называется ортогональным.

Удобно пользоваться обозначением: M = П ( M ′ ).

Ортогональное проектирование является частным случаем параллельного и обладает всеми его свойствами. Однако, если при параллельном проектировании, не являющимся ортогональным, длина проекции отрезка может быть меньше, больше или равна длине самого отрезка, то при ортогональном проектировании длина проекции отрезка не больше, чем длина самого отрезка, и длины этих отрезков связаны соотношением: П ( AB ) = | AB |•cos ϕ , где ϕ — величина угла между прямой AB и плоскостью проекций α .

Задания для работы с интернет-ресурсами

1. Наберите в поисковой системе слова «Перпендикулярность прямой и плоскости», «Перпендикуляр и наклонная к плоскости», «Наклонная и её проекция на плоскость», «Теорема о трёх перпендикулярах». На изображениях куба, параллелепипеда найдите рёбра и диагонали, перпендикулярные граням и сечениям этих многогранников. Найдите видеоролики с лекциями опытных педагогов и геометров, в которых выражаются различные взгляды как на теорию, так и на решение задач по этим вопросам.

2. Наберите в поисковой системе слова «угол между наклонной и плоскостью». Поищите задачи ЕГЭ типа С-2, в которых используется нахождение угла между прямой и плоскостью, посмотрите, как они решаются, попробуйте решить их самостоятельно. Если вам удалось найти в Интернете тренинг по решению задач этой темы, то попытайтесь им воспользоваться. Однако решать такие задачи целесообразнее после изучения темы «Расстояния в пространстве». Скоро вы изучите эту тему.

3. Изображения фигур на плоскости и в живописи подчиняются определённым законам. Найдите в Интернете такие имена, как Филиппо Брунеллески (1377—1446), Леонардо да Винчи (1452—1519) и Альбрехт Дюрер (1471—1528). Вы увидите творчество этих великих художников. Однако существует направление, которое называется импоссибилизм (impossibility — невозможность) — изображение невозможных фигур, парадоксов. Представителем этого направления живописи является известный голландский художник Мауриц Эшер (1898—1972). Найдите статьи, посвящённые его творчеству, а главное, найдите сами репродукции картин, которые представляют большой интерес и с точки зрения геометрии.

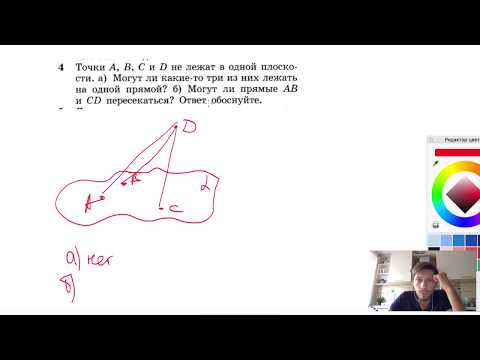
Видео:№4. Точки А, В, С и D не лежат в одной плоскости, а) Могут ли какие-то три изСкачать

Постройте проекцию правильного шестиугольника abcdeh, зная проекции трех его вершин точки a1, b1 и d1?

Геометрия | 10 — 11 классы

Постройте проекцию правильного шестиугольника abcdeh, зная проекции трех его вершин точки a1, b1 и d1.

Во — первых, задача неопределенная.

Потому что не сказано — на плоскости или в пространстве.

Примем — на плоскости.

Тогда возможны случаи, что какие — то стороны параллельны осям.

Тогда там могут быть варианты, которые решаются довольно просто.

Мы же примем, что ни одна из сторон не параллельна осям.

Расположение точек a, b, d может быть разным ( соответственно 6 — угольник может располагаться по — разному), но принцип построения есть в файле.

Если нужно «чистое» построение — сотрите вспомогательный 6 — угольник и линии проекции — получите план принципапостроения.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Точки А1 В1 — параллельные проекции вершин правильного треугольника АВС?

Точки А1 В1 — параллельные проекции вершин правильного треугольника АВС.

Точка О1 проекция его центра.

Постройте изображение треугольника АВС.

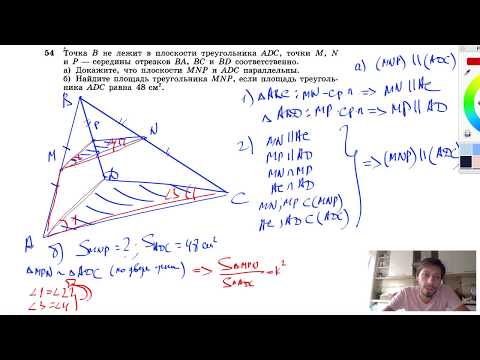
Видео:№54. Точка В не лежит в плоскости треугольника ADC, точки М, N и Р — середины отрезков ВА, ВССкачать

Доказать что три вершины правильного шестиугольника взятых через 1 , служат вершинами правильного треугольника?

Доказать что три вершины правильного шестиугольника взятых через 1 , служат вершинами правильного треугольника.

Видео:Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

. Точки А1 В1 — параллельные проекции вершин правильного треугольника АВС?

. Точки А1 В1 — параллельные проекции вершин правильного треугольника АВС.

Точка О1 проекция его центра.

Постройте изображение треугольника АВС.

Видео:№23. Точка М не лежит в плоскости прямоугольника ABCD.Скачать

Постройте проекцию правильного треугольника АВС, зная проекции его вершины А и середины К, М сторон АВ и ВС : точки А1, К1, М1?

Постройте проекцию правильного треугольника АВС, зная проекции его вершины А и середины К, М сторон АВ и ВС : точки А1, К1, М1.

Видео:№2. Отметьте три точки A, B и C не лежащие на одной прямой, и проведите прямые AB, BC и CA.Скачать

Дана точка e (2 ; — 1 ; 3)?

Дана точка e (2 ; — 1 ; 3).

Найдите координаты точки e1 проекции точки e на плоскости Oyz и координаты точки e2 проекции точки e на ось Oy.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Дана точка e (2 ; — 1 ; 3)?

Дана точка e (2 ; — 1 ; 3).

Найдите координаты точки e1 проекции точки e на плоскости Oyz и координаты точки e2 проекции точки e на ось Oy.

Видео:Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

Триугольник А1 В1 С1 — проекция треугольника АВС?

Триугольник А1 В1 С1 — проекция треугольника АВС.

Постройте проекции средних линий и медиан треугольника АВС.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Отметить три точки А1, В1, Е1 не лежащие на одной прямой?

Отметить три точки А1, В1, Е1 не лежащие на одной прямой.

Считая что эти точки являются проекциями вершин А, В, Е правильного шестиугольника АВСДЕF, постройте прекции остальных трех вершин и сторон данного шестиугольника.

Видео:№139. Из некоторой точки проведены к плоскости две наклонные. Докажите, что: а) если наклонные равныСкачать

Дана точка Е(2 ; — 1 ; 3)?

Дана точка Е(2 ; — 1 ; 3).

Найдите координаты точки Е1 — проекции точки Е на плоскости Oyz и координаты точки Е2 — проекции точки Е на ось Oy.

Видео:№90. Вершины А и В трапеции ABCD лежат в плоскости α, а вершины С и D не лежат в этой плоскости. КакСкачать

СССССРОЧНОО точки A1 и B1 — параллельные проекции вершин квадрата ABCD, точка O1 — проекция его центра?

СССССРОЧНОО точки A1 и B1 — параллельные проекции вершин квадрата ABCD, точка O1 — проекция его центра.

Постройте изображение квадрата.

Вы перешли к вопросу Постройте проекцию правильного шестиугольника abcdeh, зная проекции трех его вершин точки a1, b1 и d1?. Он относится к категории Геометрия, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Ответ : (x + 4)² + y² = 16Объяснение : Уравнение окружности с центром в точке О(х₀ ; у₀) и радиусом R имеет вид : (x — x₀)² + (y — y₀)² = R²По условию R = 4, значит точка А имеет координаты ( — 4 ; 0). Подставляем : (x — ( — 4))² + (y — 0)² = 4²(x +..

Только вместо 6 подставь свое значение 14 тр. AВD = тр. ADМ (по двум сторонам BD = DM, AD — общая, и глу между ними) АМ = АВ = 6см АС = 2АВ = 2 * 6 = 12 Ответ : 12.

Первый случай — расположение по разные стороны от прямой. Воспользуемся координатным методом. Координата нужна только одна, х, вторая, y, не важна и мы её просто не будем указывать S1(18), И1( — 8) Координата точки Щ1 найдётся как среднее арифметич..

📽️ Видео

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

№15. Три прямые попарно пересекаются. Докажите, что они либо лежат в одной плоскостиСкачать

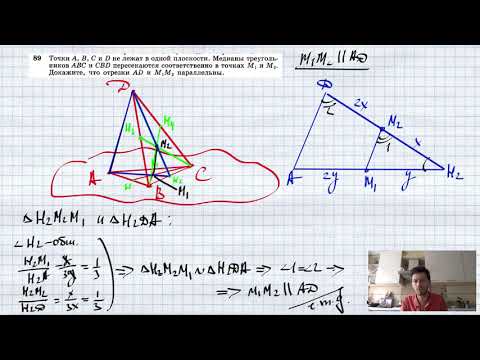
№89. Точки А, В, С и D не лежат в одной плоскости. Медианы треугольников ABC и CBD пересекаютсяСкачать

Вся суть мат. анализа за 3 мин 14 сек!Скачать

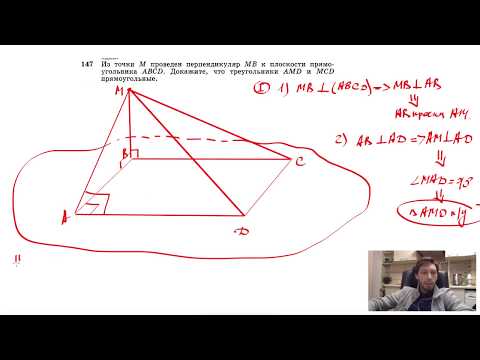
№147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

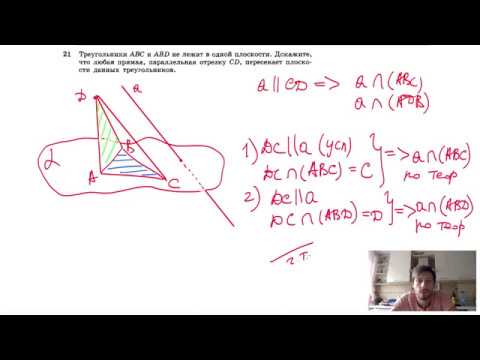
№21. Треугольники ABC и ABD не лежат в одной плоскости. Докажите,Скачать

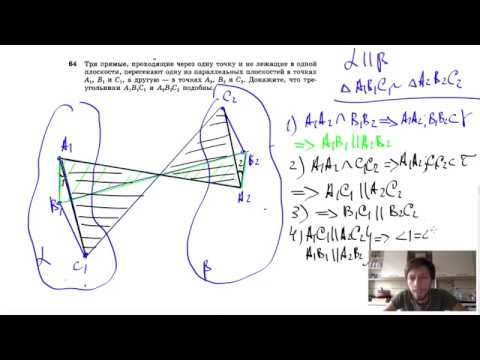
№64. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают однСкачать