Точка схода параллельных прямых ее роль в построении перспективных изображений

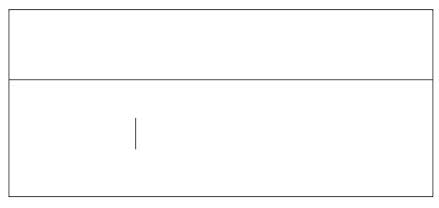
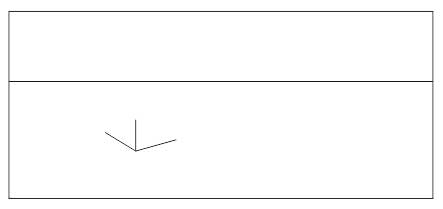
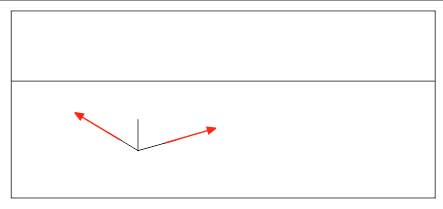
Прямая линия, принадлежащая предметной плоскости, имеет точку, беспредельно удаленную от наблюдателя, называемую «предельной точкой прямой». Рассмотрим пример построения перспективы предельной точки прямой линии (рис. 34).

Рис. 34. Перспектива бесконечно удаленной точки: а — на проецирующем аппарате, б — на картинной плоскости А = а

Проведем в предметной плоскости произвольную прямую п’ и построим перспективу двух ее точек А ‘и В’. Получим перспективу отрезка АВ заданной прямой п Продолжим отрезок в обе стороны и получим две точки пересечения: одну — с основанием картины, точку Од, другую — с линией горизонта, точку F. Точка Од — точка, в которой заданная прямая пересекает основание картины, перспектива этой точки совпадает с самой точкой. Далее будем перемещать точку вдоль прямой в предметной плоскости, удаляя ее от картинной плоскости. Тогда перспектива этих точек на картине будет перемещаться вдоль прямой Од F, занимая соответствующие положения. Луч зрения, проведенный в бесконечно удаленную точку заданной прямой, примет направление, параллельное этой прямой, и пересечет картинную плоскость в точке F. Эта точка представляет перспективу бесконечно удаленной точки заданной прямой п’. Прямая Од F не может быть продолжена на картине дальше точки F, так как лучи зрения будут приближаться к положению, параллельному прямой п’. Точка F называется перспективой предельной точки заданной прямой. Отсюда следует, что все параллельные прямые имеют одну общую точку- перспективу предельных точек этих прямых. Она называется точкой схода параллельных прямых. Исключение составляют прямые, расположенные в предметной плоскости параллельно картине: они не имеют картинного следа и точки схода, так как ей параллельны.

Если взять несколько пучков параллельных прямых, принадлежащих предметной плоскости, то для каждого пучка будет своя точка схода. Но все эти точки схода будут расположены на линии горизонта на одинаковой высоте. Высота точек будет соответствовать высоте точки зрения, поскольку лучи зрения, направленные в предельную точку, будут параллельны предметной плоскости (рис. 35). Отсюда следует, что для любой прямой, лежащей в предметной плоскости, перспектива предельной точки отстоит от основания картины на расстояние, равное высоте точки зрения. Совокупность перспектив предельных точек всех прямых, лежащих в предметной плоскости, представляет собой прямую, расположенную параллельно основанию картины и отстоящую от нее на расстояние, равное высоте точки зрения. Эта прямая является линией горизонта и перспективой предельной прямой предметной плоскости. Она ограничивает на картине изображение предметной плоскости со всеми точками и прямыми, ей принадлежащими.

Перспективу предельной точки прямой линии можно построить на проецирующем аппарате следующим образом:

• 1) провести луч зрения, параллельно заданной прямой линии;
• 2) построить его проекцию на предметную плоскость;
• 3) провести плоскость, проецирующую к предметной плоскости, через построенные прямые линии;

Рис.35. Перспектива бесконечно удаленных точек параллельных прямых:

а — на проецирующем аппарате; б — на картинной плоскости

4) найти линию пересечения этой плоскости с картинной плоскостью;

5) найти точку пересечения полученной линии и проецирующего луча, точка F, данная точка и есть перспектива предельной точки прямой линии, расположенной в предметной плоскости.

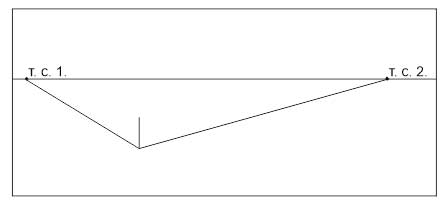
Используя алгоритм построения предельных точек прямых, построим перспективу угла (рис. 36), образованного двумя пересекающимися прямыми, лежащими в предметной плоскости.

Рис. 36. Перспектива угла:

а — на проецирующем аппарате; б — на картинной плоскости

Перспектива предельной точки параллельных прямых является для них точкой схода. На рис. 37 приведен пример построения точки схода для прямых, расположенных под углом 45° к картинной плоскости. Такими точками являются дистанционные точки.

Дистанционные точки D и D, или точки отдаления, располагаются на линии горизонта слева и справа от точки Р на одинаковом расстоянии, равном

Рис. 37. Перспектива прямой, расположенной под углом 45° к картине: а — на проецирующем аппарате; б- на картинной плоскости расстоянию от точки зрения до картины. Проведем в предметной плоскости прямую т’ под углом 45° к картинной плоскости и построим точку А — перспективу одной из точек (А’) заданной прямой т’. С этой целью в предметной плоскости продолжим прямую т ‘до пересечения с основанием картины в точке Ch. Соединим точку А и точку О2 и продолжим полученную прямую до пересечения с линией горизонта. Прямая О2А пересечет картинную плоскость в точке D. Если перемещать точку Л ‘вдоль прямой в предметной плоскости, удаляя ее от картинной плоскости, то перспективой предельной точки прямой будет являться дистанционная точка D.

Задание. Для закрепления материала постройте самостоятельно перспективу прямой линии, предельной точкой которой будет дистанционная точка D, используя рис. 37.

Восходящая прямая — прямая, которая возвышается над предметной плоскостью по мере ее удаления от картины. Перспектива предельной точки восходящей прямой располагается выше линии горизонта. Построить ее можно следующим образом (рис. 38, 39).

Рис. 38. Перспектива восходящей прямой: а — на проецирующем аппарате; б — на картинной плоскости

Рис. 40. Точка схода

На прямой выделим отрезок А’ и В’ и по-

Рис. 39. Пример перспективы строим его проекцию (отрезок а’Ь’> на предметную плоскость. Теперь находим перспективу предельной точки этой прямой как линии, принадлежащей предметной плоскости (см. рис. 35). Перспективой предельной точкой прямой а’ Ь’ является точка f. Из этой точки строим прямую, перпендикулярную к предметной плоскости, а из точки зрения проводим луч, параллельный заданной восходящей прямой (отрезку А’ и В’). Пересечением этих двух прямых будет точка F, которая и является перспективой предельной точки заданной прямой и точкой схода всех прямых, расположенных параллельно этой прямой.

Нисходящая прямая — прямая, которая снижается над предметной плоскостью по мере ее удаления от картины. Перспектива предельной точки нисходящей прямой располагается ниже линии горизонта.

Задание. Для закрепления материала постройте самостоятельно перспективу отрезка нисходящей прямой линии, используя свойства перспективы.

Для прямых, лежащих перпендикулярно картине, точкой схода будет являться главная точка картины — точка Р, так как она лежит на перпендикуляре, проведенном из точки зрения к картине, а перпендикуляр и есть прямая, параллельная заданному направлению (рис. 40).

Видео:Перспективные изображения: принцип построения перспективы точки и прямой, понятие ФОКУССкачать

Перспектива

Вступление

В этой статье я попытаюсь объяснить, как строятся рисунки с перспективой и как различные типы перспективы используются для выделения тех или иных аспектов композиции. Здесь приведены мои собственные иллюстрации, большинство из которых нарисованы по соответствующей модели AutoCAD (для точности) или взяты непосредственно из этой программы. Для наглядности рисунки выполнены в линиях.

Что такое перспектива

Перспектива учитывает, откуда мы смотрим на сцену, что эта сцена собой представляет и какую её часть мы видим. Законы перспективы описывают, как сходятся прямые и уменьшаются предметы по мере удаления.

Законы перспективы были разработаны в эпоху Возрождения. Они позволили художникам с точностью изображать сцены, которые они наблюдали из определённой точки. До Возрождения иногда встречались картины, где объекты на переднем плане были больше, чем на заднем, но никто толком не понимал этих правил, поэтому изображения были неточными. Теперь в нашем распоряжении есть законы перспективы, и мы можем прибегнуть к ним для достижения большего реализма в рисунках.

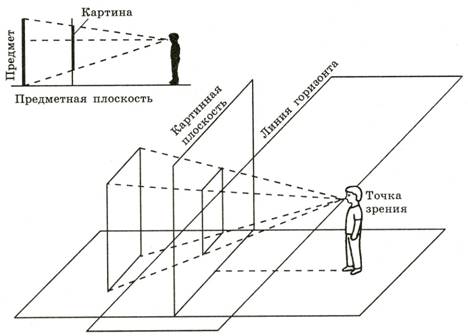
Проекция сцены на трёхмерную плоскость

Когда мы рисуем, мы проецируем реально существующую или воображаемую трёхмерную сцену (будто бы наблюдаемую из определённой точки) на плоскость: холст или лист бумаги. Каждая линия или геометрическая форма находит своё отражение в рисунке. Это как если бы мы поместили мощный прожектор перед сценой, а позади неё — огромный экран (называемый картинной плоскостью), уходящий даже в землю. Прожектор освещал бы сцену, а она отбрасывала бы тень на экран (на картинную плоскость). Объекты, что находятся вблизи прожектора, будут отбрасывать большие тени, а те, что вблизи экрана, — тени размером с самих себя.

Изображение, получаемое таким образом на экране, — это изображение в перспективе. Оно показывает сцену такой, какой она видится оттуда, где находится прожектор. В разных книгах и графических пакетах эта позиция называется по-разному (точка наблюдения, камера, глаз).

Точки схода

Все прямые, которые параллельны в трёхмерной сцене, будут при перспективном изображении сходиться в одной точке. Это точка схода. Каждая группа параллельных прямых (параллельных между собой, но непараллельных прямым из другой группы) имеет свою точку схода на рисунке. У прямых, лежащих в плоскости земли или параллельных ей, точки схода всегда находятся на линии горизонта.

Исключение составляют прямые, параллельные картинной плоскости. Они не сходятся. Примером служат вертикальные прямые на рисунке вверху. Они так и остаются вертикальными.

Если посмотреть на трёхмерную сцену, то покажется, будто горизонтальные прямые сходятся в како-то точке на горизонте (её точное местонахождение будет зависеть от ориентации прямых относительно наблюдателя). Представьте себе несколько параллельных горизонтальных прямых, лежащих в одной вертикальной плоскости (например, полосы раствора в кирпичной стене) и сходящихся в одной точке на горизонте. Точно под этой точкой или точно над ней будет сходиться диагональ этой плоскости с параллельными ей прямыми. Это соотношение полезно для определения размеров объектов в перспективе.

Сходящиеся прямые и точки схода — не просто какая-нибудь условность, к которой прибегают художники. Это явление на самом деле имеет место. Параллельные прямые действительно кажутся сходящимися, если посмотреть на них под углом. Как-нибудь найдите себе кирпичную стену, встаньте напротив её и хорошенько приглядитесь. Если вы будете смотреть на неё прямо, полосы раствора покажутся параллельными, но если вы повернёте голову, создастся ощущение, будто они сходятся в точке на горизонте.

Другие особенности рисования в перспективе

Если вы внимательно посмотрите на окружающий мир, то заметите и другие особенности перспективы, помимо того, что параллельные прямые сходятся. По мере удаления объекты уменьшаются. Кажется, что чем дальше находятся равноудалённые друг от друга предметы (например, телефонные столбы или железнодорожные шпалы), тем теснее они расположены. Вдалеке наземные объекты настолько малы, что с трудом различимы. При ещё большем удалении они и вовсе превращаются в точки. Существуют методики построения линий и других геометрических форм, позволяющие реалистично воспроизвести на рисунке этот эффект. Вы сможете вполне убедительно его сымитировать, если имеете хоть какое-то представление о перспективе.

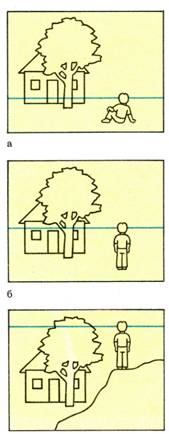
Считается, что линия горизонта находится на уровне глаз наблюдателя. Если человек стоит на земле в окружении людей (которые тоже стоят), линия горизонта будет находиться приблизительно на уровне глаз окружающих: пониже у высоких людей, повыше у низких. Предметы, высота которых не достигает уровня глаз наблюдателя, будут находиться ниже линии горизонта, и их верхние грани будут видны хотя бы чуть-чуть. Предметы, целиком расположенные выше уровня глаз, окажутся выше линии горизонта, и, хотя бы немного, но будут видны их нижние грани. По мере удаления они будут опускаться к линии горизонта и грани, обращённые к наблюдателю, будут видны полнее.

В трёхмерной сцене будут искажены все геометрические формы за исключением тех, которые параллельны картинной плоскости. Такие формы не искажаются, но изменяются в размерах в зависимости от того, на каком расстоянии находятся.

Остальные геометрические формы искажаются. Окружности превращаются в эллипсы. Если окружность служит основанием конуса или цилиндра, малая ось эллипса совпадает с их осью.

Одно-, двух- и трёхточечная перспектива

Любой рисунок предполагает несколько точек схода, например, одна для фасада здания, одна для торца, одна для меча героя, одна для копий в надвигающейся на него шеренге солдат, одна для боковой части повозки, которую защищает герой. Может получиться так, что множество прямых идут в разных направлениях, и ни одно из них нельзя выделить как главное. Или изображённых объектов недостаточно, чтобы выявить хотя бы одну точку схода. Примером может служить абстрактный рисунок или вид планеты из космоса. Однако в особо реалистичных изображениях одна, две или три точки схода наверняка выделяются на фоне остальных.

Одноточечная перспектива

Предметы направлены на зрителя

Когда взгляд художника направлен в главную и единственную точку схода, такая перспектива называется одноточечной. Сюда относятся ситуации, когда мы смотрим в тоннель, в пушечный ствол, на вершину небоскрёба (стоя у его подножья). Такой перспективой пользуются, когда хотят обратить внимание зрителя на точку, где сходятся прямые. Ещё этот приём как бы затягивает зрителя внутрь картины. В рисунке с одноточечной перспективой кажется, что предметы нацелены на зрителя либо находятся по бокам от зрителя и уходят вдаль.

Некоторые художники избегают одноточечной перспективы. Им кажется, что у зрителя возникает ощущение, будто ему что-то навязывают, заставляют смотреть не туда, куда ему хочется. Если одноточечную перспективу использовать не по назначению, она может нагонять скуку. Например, не стоит изображать в одноточечной перспективе стену. Вообще, стена — довольно заурядный предмет, чтобы разглядывать его в упор.

Конечно, вам придётся руководствоваться здравым смыслом. Вам может показаться, что в данном случае одноточечная перспектива выглядит занятно или что данный предмет хорошо смотрится именно в таком ракурсе. Ещё вы можете выбрать одноточечную перспективу для конкретной картины, потому что она берёт зрителя в плен или потому что создаёт ощущение неподвижности.

Двухточечная перспектива

Гораздо чаще встречается двухточечная перспектива. Например, это может быть сцена на улице, где здания и другие объекты уменьшаются по направлению к горизонту, или сцена в помещении, где стены и предметы интерьера окружают зрителя. В двухточечной перспективе взгляд зрителя обычно бывает направлен параллельно земле, поэтому вертикальные прямые не сходятся. Рисунок вверху слева как раз такой. Зрителя никуда не затягивают, его взгляд не устремлён вниз по коридору и не упирается в стену. Напротив, сцена простирается в нескольких направлениях. Предметы здесь расположены под углом, а не вдоль одной оси. Такой рисунок обычно представляет собой декорации, на фоне которых разворачивается действие, где внимание зрителя не сконцентрировано на отдельно взятой точке.

Заметьте, что, изображая сцену в помещении, нужно учитывать, как центр взгляда вписывается в комнату. Обычно вам не нужно, чтобы зритель смотрел прямо в угол или прямо из угла. У зрителя может возникнуть ощущение, будто его поставили туда в наказание.

Обычно в двухточечной перспективе имеются левая и правая точки схода. Реже встречается двухточечная перспектива с верхней и нижней точками схода. Скорей всего, вы прибегнете к помощи последней, если захотите создать у зрителя ощущение, будто он идёт вперёд по прямой, но смотрит вверх, а не на горизонт. Линии, параллельные прямой, по которой он идёт, будут иметь точку схода на горизонте, но и вертикальные прямые также будут сходиться. Этим подчёркивается высота. Примером служит рисунок вверху справа.

Трёхточечная перспектива

Чтобы подчеркнуть высоту

Трёхточечную перспективу построить сложнее. Она встречается реже, так как подразумевает, что зритель смотрит на сцену снизу или сверху, а не прямо. К такой перспективе обращаются, когда нужно не только дать полную картину происходящего, но и сделать акцент на вертикальном измерении (таков замысел художника на рисунке вверху слева). Трёхточечной перспективой следует пользоваться и когда вы пытаетесь подчеркнуть равноправность всех трёх измерений, например, на рисунке вверху справа, изображающем сцену в открытом космосе, где нет таких понятий, как верх и низ.

Угол зрения

Угол зрения 20 градусов

Угол зрения показывает, какая часть сцены попадает на рисунок при данной точке наблюдения, направлении взгляда и картинной плоскости. Чем шире угол зрения, тем большая часть окружения видна и тем сильнее увеличивается рисунок (тем сильнее уменьшаются предметы, если размер рисунка остаётся постоянным).

Если вы работаете с определённым размером бумаги и вам нужно расширить угол зрения, не изменяя при этом размеров персонажа, вы можете придвинуть точку наблюдения ближе к персонажу. При расширении угла зрения одновременно с приближением какого-то объекта, расстояние между точками схода сокращается, и все остальные предметы уменьшаются в размерах по сравнению с этим объектом. Это видно из вышеприведённых рисунков. Оба представляют собой изображения простой трёхмерной модели, сделанной в AutoCAD Release 13. На рисунке слева угол зрения мал, сравним с углом зрения обычного фотоаппарата. На рисунке справа представлена та же модель, но точка наблюдения находится ближе к группе людей, и угол зрения шире. Таким способом на картине можно выделить персонажа или предмет, обратить на него внимание и придать ему монументальность. Заметьте, что изображение персонажа слегка изменится: больше будут видны ступни, низ шляпы и так далее. Хотя на рисунке персонаж будет занимать примерно столько же места.

Только не стоит этим приёмом злоупотреблять. Он может быть уместен в батальной сцене, где нужно обратить внимание на главнокомандующего, и совсем не нужен в более мирной обстановке, например, в сцене с влюбленной парой. Постоянно использовать слишком широкий угол зрения — всё равно что ставить восклицательные знаки в конце каждого предложения.

Ещё одна проблема заключается в том, что при больших углах по краям изображения появляются сильные искажения. Это сбивает с толку и раздражает. Оцените рисунок. Приведённый ниже. Его угол зрения составляет около 150 градусов — явный перебор. Комната, которая здесь изображена, квадратная, хотя из рисунка сложно понять даже это. На самом деле, многие люди, видя этот рисунок, не верят, что комната квадратная. Но если внимательно присмотреться, можно заметить, что края ближней правой и дальней левой стены сходятся в одной точке, что может быть только если они параллельны. Поэтому углы в комнате прямые, а такие сильные искажения — из-за непомерно большого угла зрения.

Угол зрения 150 градусов

В большинстве рисунков из этой статьи применяется большой угол зрения: от 90 до 150 градусов и более. Это сделано с целью лучше иллюстрировать перспективные сокращения. Вы, вероятно, будете использовать меньший угол зрения, чтобы свести искажения к минимуму. Рекомендуется делать угол зрения меньше 90 градусов и даже меньше 60, если вам это удастся. Для двухточечной перспективы это означает, что хотя бы одна точка схода лежит за пределами рисунка.

Не рекомендуется использовать угол зрения более 90 градусов. Что касается 180 и более градусов, то это вообще невозможно при работе по методикам, описанным в этой статье (правильный термин для них — линейная перспектива). Вы не можете нарисовать на плоском листе бумаги то, что находится позади вас. Существуют методики создания изображения с углом зрения больше 180 градусов, но, насколько я понимаю, рисовать приходится на сферической поверхности, а потом проецировать рисунок на плоскость. Результат похож на фотографию, сделанную с помощью линзы «рыбий глаз». Рисунок строится по совершенно другим правилам. Если в трёхмерном пространстве линии прямые, то на получившемся рисунке они будут искривлены. Пучок прямых может исходить из тоски в левой части рисунка, затем расходиться и вновь сходиться в точку в правой части. Такой тип перспективы более сложен и не рассматривается в этой статье. Вообще, в большинстве книг, которые мне попадались, о нём ничего не сказано.

Определение размеров в перспективе

Продливаем линии чтобы определить высоту

В перспективе определить размер предметов достаточно сложно. Даже если на самом деле он одинаков, в перспективе он может различаться. К счастью, если вы правильно построили предмет в одном месте, вы можете продлить линии построения и узнать, как он будет выглядеть в другой части рисунка. Это показано на рисунке вверху слева. Если у нас получится точно изобразить вора на переднем плане, мы сможем определить, каких размеров будет ничего не подозревающая жертва на заднем плане. Мы проведём касательные к голове и ступням вора влево, затем перпендикулярно им построим прямые вверх по улице до того места, где будем рисовать жертву.

Мы также можем достраивать линии, чтобы легче было нарисовать тротуарные плитки, кирпичную кладку, забор, колонну пехотинцев и другие предметы, расположенные рядами. Начните с выбора прямой, параллельной картинной плоскости в трёхмерной сцене. Затем определите положение этой прямой на рисунке, разбейте её на равные отрезки и сделайте засечки, как на вертикальной прямой на рисунке вверху посредине. Проведите прямые от засечек до точки схода. Нарисуйте на глаз один кирпич. Диагональ этого кирпича будет служить диагональю ещё многим кирпичам, что позволит вам правильно определить их размер. Ваших знаний теперь достаточно, чтобы адекватно изобразить все или почти все кирпичи на рисунке. Чтобы нарисовать кирпичи, находящиеся в дальнем конце стены, проведите ещё диагонали. Все диагонали должны сходиться в точке, которая находится прямо над точкой схода прямых, проведённых от засечек, или прямо под ней.

Если предметы расположены в ряд, например, столбики забора или колонна пехотинцев, мы можем изобразить третий элемент ряда, основываясь на расстоянии между первыми двумя элементами. Сперва постройте прямые от вершины, середины и основания элемента к точке схода. Затем проведите прямую через вершину первого элемента и середину второго. Продлите её до пересечения с линией оснований. Из этой точки и рисуется следующий элемент.

Воздушная перспектива

Порт в ясный день

Иногда она называется туманом. Удалённые объекты кажутся подёрнутыми дымкой (по цвету приближаются к светло-серому) из-за испарений, дыма и других атмосферных эффектов. Воздушная перспектива должна усиливать ощущение дальности, создаваемое линейной перспективой. Из двух картинок вверху, на правой порт кажется чуть дальше, чем на левой. Что касается размеров, то предметы на картинках (скопированных с одного оригинала) совершенно одинаковые. Но на правой картинке туман слегка обволакивает берег и, хочется верить, немного уменьшает надежду на благополучное прибытие в порт.

Воздушная перспектива изменяется в зависимости от погодных условий, местности и, разумеется, желания художника. Если вы рисуете панораму сказочного города, может быть, вам и не захочется использовать воздушную перспективу, чтобы город предстал во всей своей красе. Но если это туманное болото или подводный мир, воздушная перспектива будет у вас ярко выражена.

Воздушная перспектива служит показателем расстояния. Однако у неё есть и другие не менее важные функции. Она помогает заострить внимание на переднем плане, поскольку здесь предметы чётче и контрастнее, чем на заднем плане. С её помощью можно создать ощущение смутного, полусонного восприятия, где настроение преобладает над деталями. Этот приём хорошо освоен импрессионистами.

Ещё раз об основных положениях

• В рисунках с перспективой действуют некоторые правила, за выполнением которых нужно внимательно следить. Вот они:
• В общем случае, прямые, параллельные в трёхмерном пространстве, на рисунке будут сходиться в одной точке.
• Чем дальше находятся равноудалённые друг от друга предметы, тем теснее они будут располагаться на рисунке.
• Геометрические формы, если мы смотрим на них прямо, не искажаются, изменяются только их размеры, причём пропорционально.
• Если линии в трёхмерном пространстве прямые, они также будут прямыми в перспективе (при условии, что угол зрения меньше 180 градусов). Точки, лежащие на одной прямой, в перспективе по-прежнему будут лежать на одной прямой, а точки касания останутся точками касания. Это поможет вам при определении размера кирпичей, плиток и т.д. и при рисовании кривых.
• Если в трёхмерном пространстве плоскость вертикальна, то все лежащие в ней прямые будут сходиться в точке на горизонте. Любая другая группа параллельных прямых, лежащих в этой же плоскости, будет сходиться в точку прямо над этой точкой горизонта или прямо под ней.

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Урок 3. Линейная перспектива. Построения, часть 1.

Без знания законов линейной перспективы невозможно реалистично изобразить ни один объемный предмет, будь то человек или табуретка.

Но пугаться не стоит. Несмотря на громкое название, основных законов всего два и запомнить их очень просто.

Все вы когда-нибудь ездили на электричке и переходя железнодорожные пути, смотрели не идет ли поезд. Что вы видели в этот момент?

Сходящие на линии горизонта рельсы, очевидно, параллельные друг другу.

И одинаковой высоты столбы линии электропередач, ближний из которых кажется значительно больше дальнего.

Собственно, это и есть два основных закона линейной перспективы:

1. Параллельные прямые, удаляющиеся от нас мы видим сходящимися в одной точке. Эта точка называется точкой схода. Она, или ее проекция находится на линии горизонта
2. Предметы одинаковой величины кажутся тем меньше, чем дальше от нас они расположены.

Видео:Уловая перспектива. Точки схода. Линия горизонта. Рисование для начинающиех. Interior SketchСкачать

Основные понятия перспективы.

Перед тем, как мы начнем применять эти законы на практике, я дам вам несколько определений. Это упростит объяснения и поможет вам легче понимать специальную литературу.

Горизонт ( линия горизонта) — плоскость, горизонтальная, бесконечная, находящаяся на высоте глаз наблюдателя и ВСЕГДА видимая в виде прямой горизонтальной линии.

Условно можно считать, что перспективный горизонт и горизонт географический в нашем зрении совпадают.

Все предметы, находящиеся ниже этой плоскости, ниже горизонта, мы видим сверху; все предметы, находящиеся выше горизонта,- видим снизу.

Важно запомнить, что линия горизонта всегда находится на уровне ваших глаз. Если вы сядете на землю, то перспективный горизонт опустится вместе с вами, при подъеме в гору он поднимается.

Точка зрения – условное расположение взгляда художника относительно изображаемого объекта.

Картинная плоскость — условная плоскость, на которую проецируется изображение. Она всегда вертикальна. Независимо от того, как расположен ваш лист.

Сокращения. Если поверхность находится под углом к картинной плоскости, она нам кажется более узкой, чем когда она параллельна картинной плоскости. Этот эффект называется — сокращения. Чем ближе угол между плоскостями к 90 градусам, тем больше сокращения. Если угол равен 90 градусам, мы видим поверхность, как линию.

Видео:Перспектива. Метод архитекторовСкачать

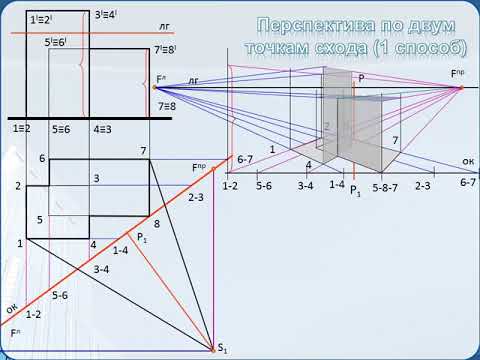
Основные понятия. Тест.

Чтобы закрепить полученные знания, предлагаю вам пройти небольшой тест. Ответы присылайте, пожалуйста, мне в личном сообщении.

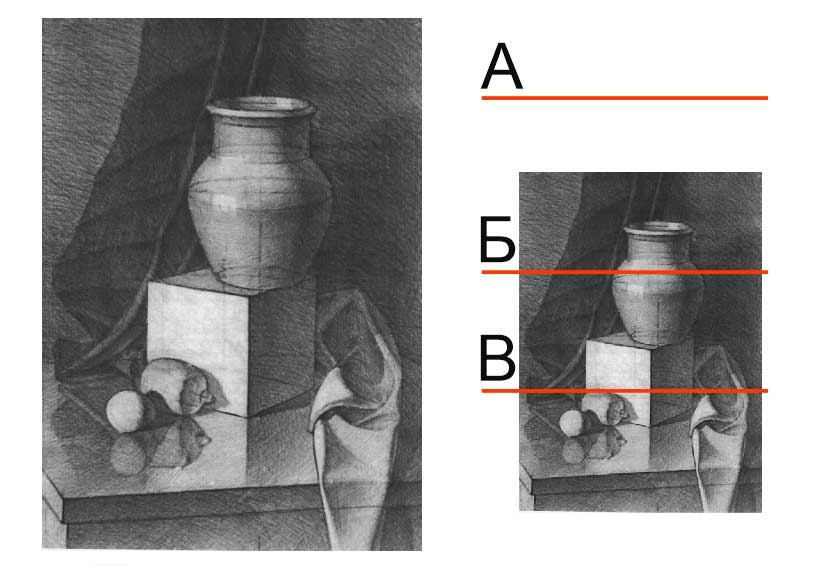
1. Где находится линия горизонта на картине.
   1. А
   2. Б
   3. В
   4. В натюрморте ее нет, горизонт виден только в пейзаже.
2. Картинная плоскость…
   1. … всегда совпадает с плоскостью листа, на котором вы работаете.
   2. … может совпадать, если лист расположен вертикально и прямо перед вами.
   3. … никогда не совпадает.
3. Геометрические тела в натюрморте находятся …
   1. … на линии горизонта.
   2. … выше линии горизонта.
   3. … ниже линии горизонта.
   4. … и выше и ниже.

Видео:Практические способы построения параллельных прямых | Геометрия 7-9 класс #29 | ИнфоурокСкачать

Перспектива с одной точкой схода.

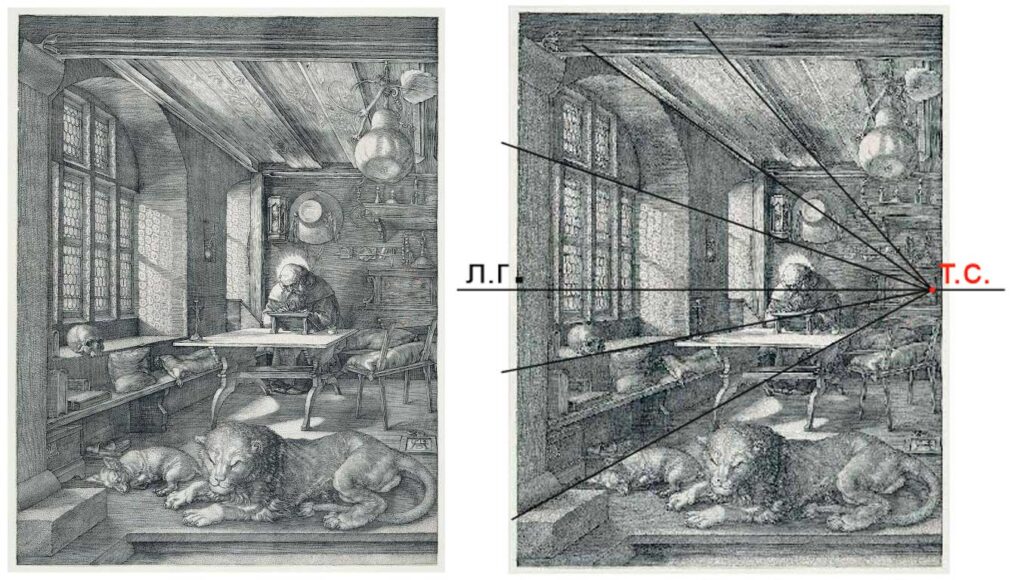
Один из двух наиболее распространенных типов перспективных построений. Мы ее используем, когда рисуем объект с прямыми углами, передняя сторона которого параллельна картинной плоскости. Этот тип построений часто используется для изображений интерьеров и архитектуры.

Saint Jerome in His Study Albrecht Dürer 1514

Видео:Построение перспективного изображения методом архитекторов: требования к точке стояния и углу зренияСкачать

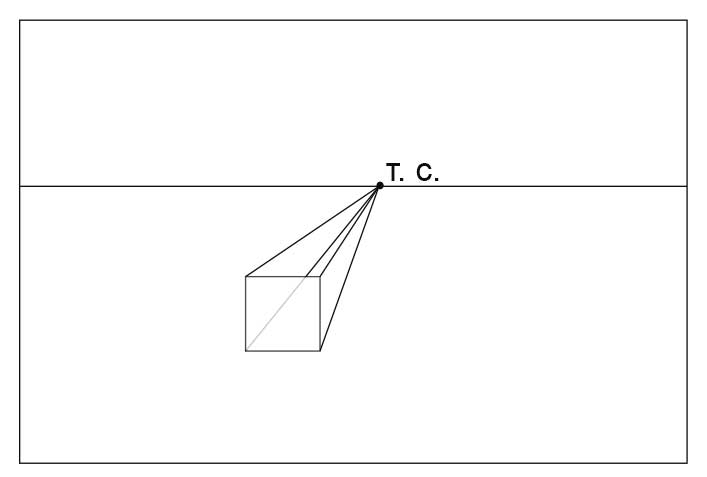
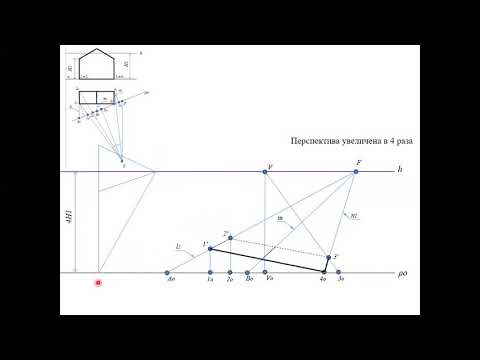
Разберем построения перспективы с одной точкой схода на примере построения куба.

• Нарисуем на нашем листе линию горизонта. Местоположение выбираем произвольно, лучше в середине или верхней трети листаю
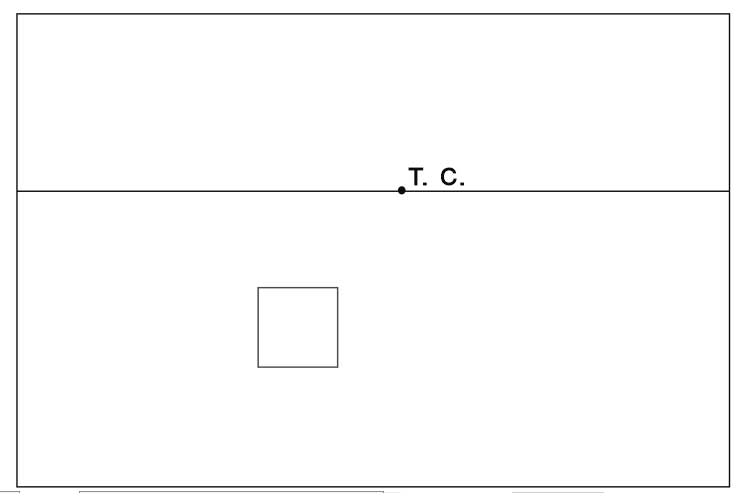
• Нарисуем переднюю сторону куба, ниже линии горизонта.Она будет видна нам без искажений, то есть как квадрат.

• Зададим точку схода (Т.С.) на линии горизонта. Когда мы рисуем по воображению, мы ее задаем произвольно. При натурном рисовании, она зависит от нашей точки зрения и определяется по параллельным прямым в изображаемом объекте.

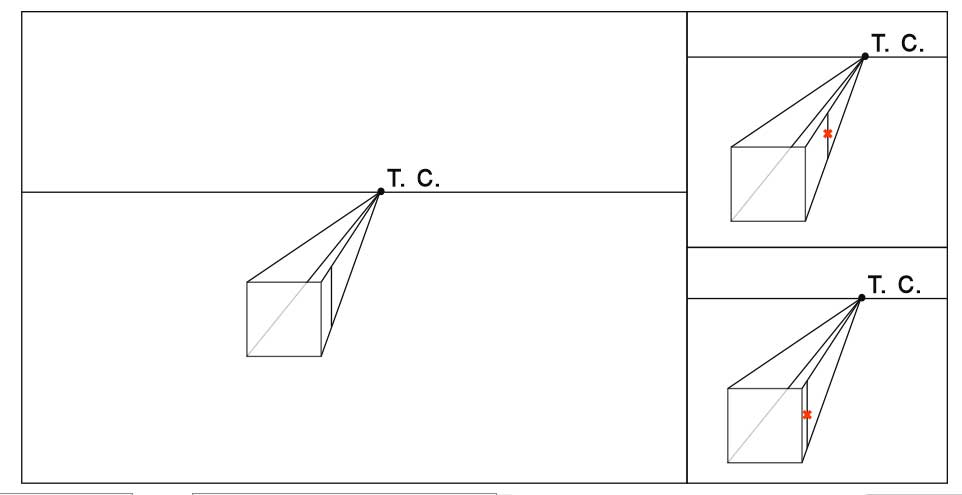
• Уходящие от нас ребра куба параллельны друг другу, а значит сходятся на линии горизонта в точке схода. Проведем прямые из углов передней стороны куба в точку схода.

• Определим на глаз длину уходящих от нас ребер куба. Мы видим их в сокращении. Справа от рисунка показаны ошибка при определении длины.

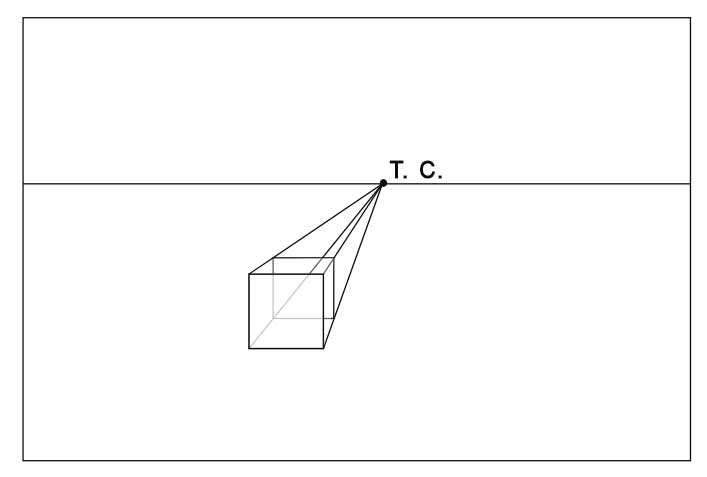
• Достраиваем дальнюю сторону куба. Обратите внимание, что она тоже видна нам без искажений, то есть, как квадрат.

Видео:Метод Архитекторов с одной точкой схода. Семестровая работаСкачать

Упражнение 1.

Постройте кубы на линии горизонта и выше нее.

Видео:ТЕМА 1. ОСНОВЫ ПЕРСПЕКТИВЫСкачать

Дополнительное упражнение 1.

Распечатайте работы, восстановите построение и найдите, где проходит линия горизонта.

Видео:Построение перспективы с одной точкой схода. Упражнение1Скачать

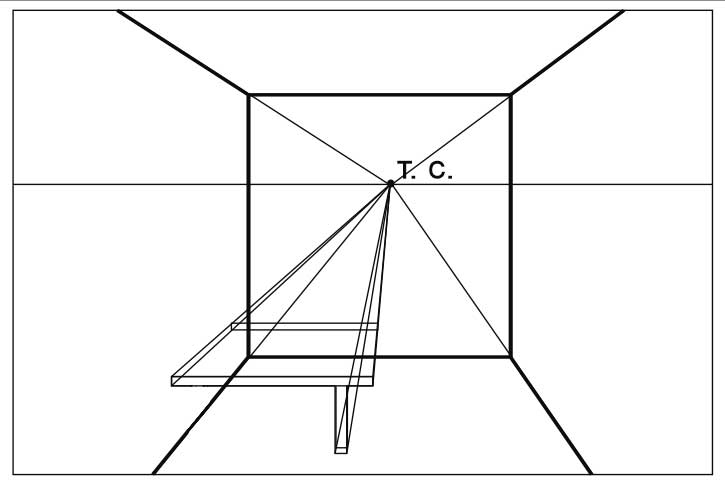
Дополнительное упражнение 2.

Постройте недостающие ножки у стола.

Видео:Лекция 7. Перспектива. Часть 1.Скачать

Перспектива с двумя точками схода.

Это более распространенный тип перспективных построений. Мы им пользуемся тогда, когда изображаем объекты, стороны которых расположены под прямым углом друг к другу. Сами эти объекты могут находиться под произвольными углом к картинной плоскости.

Обратите внимание, что несмотря на название типа построения, на одной работе точек схода может быть бесконечно много. Потому что для каждой группы параллельных прямых точка схода своя. Если у вас на работе несколько предметов, расположенных под разным углом к картинной плоскости, групп параллельных прямых тоже будет несколько.

View of Warsaw from the Terrace of the Royal Castle
Bernardo Bellotto1773

В одной работе могут совмещаться построение перспективы с одной и с двумя точками схода.

В системах построения с одной и с двумя точками схода мы условно считаем все вертикали строго вертикальны. Мы не учитываем, что вы смотрите на объект сверху или снизу и, соответственно, один из его краев ближе к вам, а вертикальные грани являются параллельными прямыми, удаляющимся от вас и должны иметь точку схода. Если вы хотите учитывать этот фактор, вам нужно использовать систему построения с тремя точками схода. Но о ней и о других системах построения объемных изображений мы будем говорить в следующем курсе.

Видео:Как найти точки схода на натуре.Скачать

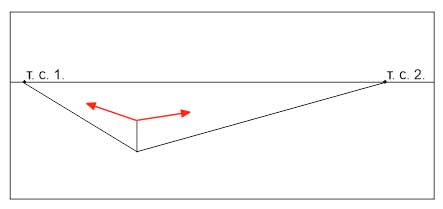
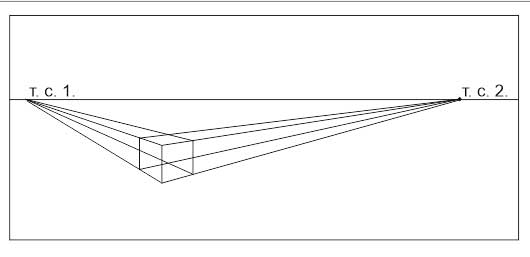
Разберем построения перспективы с двумя точками схода на примере куба.

• Проводим линию горизонта по центру листа или чуть выше.
• Произвольно задаем длину переднего вертикального ребра куба.

• Задаем направления горизонтальных, уходящих от нас, ребер куба. Углы выбираем произвольно, но стараемся, чтобы визуально угол между ребрами читался как прямой. (Он не будет прямым в геометрическом смысле, так как он находится не в плоскости, параллельной картинной, и мы видели его с перспективными искажениями)

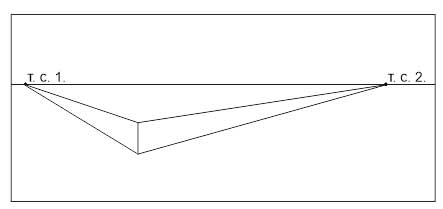
• Продлеваем горизонтальные ребра до линии горизонта. На пересечении получаем две точки схода (Т.С1 и Т.С.2).

• От верхнего края переднего ребра проводим линии в точки схода.

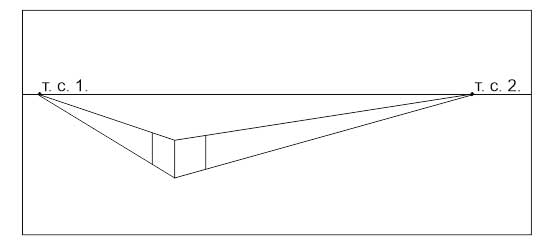
• На глаз определяем ширину боковых сторон куба. Обратите внимание, что их ширина будет меньше высоты, так как мы видим ее в сокращении, а высоту- нет. Чем на вашем рисунке меньше угол между горизонтальным и вертикальным ребром, тем уже соответствующая сторона.

• От дальних углов боковых поверхностей проводим линии в точки схода.

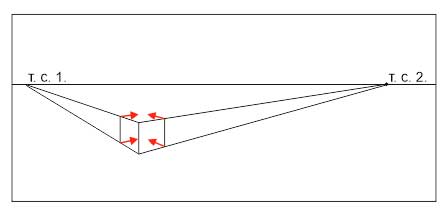
• На пересечении получаем верх и низ дальнего вертикального ребра. Соединяем их — строем ребро.

Видео:Как рисовать "Перспективу и Пространство" - А. РыжкинСкачать

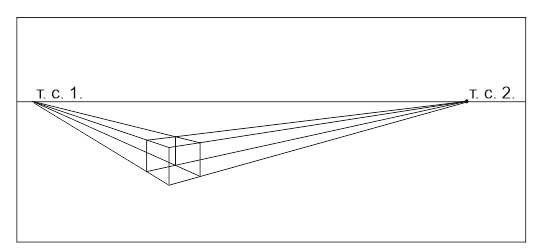
Упражнение 2.

Постройте кубы на и выше линии горизонта с теми же точками схода.

Видео:Изображение пространства. Правила построения перспективы. Воздушная перспектива.Скачать

Задание. Воображаемый интерьер.

То, что окружает человека иногда говорит о нем больше, чем его внешность. Мне бы хотелось, чтобы вы придумали интерьер «с характером»: пространство, глядя на которое понимаешь, кто там обитает или что там произошло. Хотя ни обитателей ни событий мы не видим.

Как примеры тем предлагаю:

» комната, где прячется преступник»

«комната одинокого человека»

«комната, где находят ответы на вопросы»

Если вы боитесь не справиться с интерьером, можно взять упрощённый вариант задания — предмет мебели, по которому можно узнать владельца, Например: » любимое кресло старого профессора». Можно пофантазировать на тему любимых предметов мебели литературных героев.

Видео:Основы линейной перспективыСкачать

Дополнительное упражнение 3.

Даже мастера путались в построениях.

Распечатайте картины, восстановите линии построения и найдите, где ошиблись художники.

Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

Дополнительное задание.

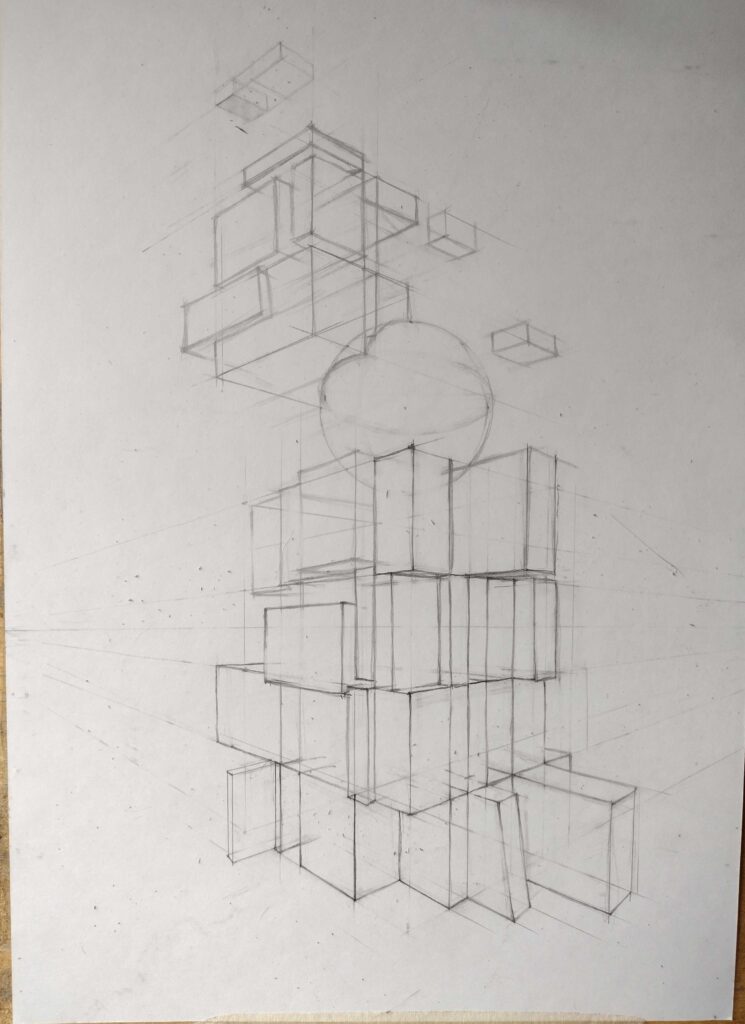
Композиция из геометрических тел. Линейный рисунок без тона. Основные элементы строим напросвет( так, как будто они из стекла) Стараемся пока использовать только кубы или прямоугольные параллелепипеды.

Кубы построены напросвет

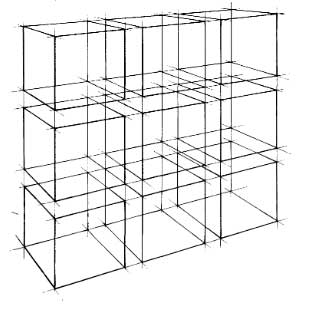
Предлагаю вам вообразить себя архитектором или скульптором-абстракционистом и придумать интересную и эстетичную конструкцию из геометрических тел. Вы можете создать просто гармоничную структуру или попробовать изобразить абстрактное понятие, например, тяжесть или легкость, величие, власть или угрозу. Любые, даже самые необычные варианты, приветствуются.

💡 Видео

Основы перспективы в рисунке. Учимся изображать объем и пространство на плоскости!Скачать

Лекция 7. Перспектива. Часть 2.Скачать

Построение перспективы с одной точкой схода. Упражнение 2Скачать

"Пейзаж. Правила построения линейной и воздушной перспективы".Скачать

Основной закон перспективы. Линия горизонта. Учимся рисоватьСкачать