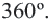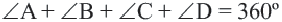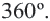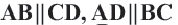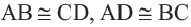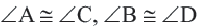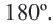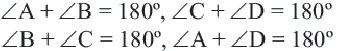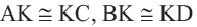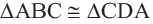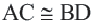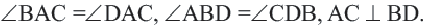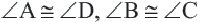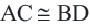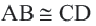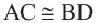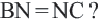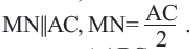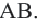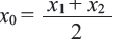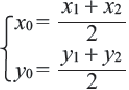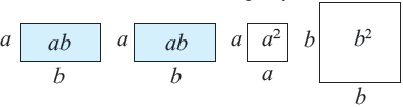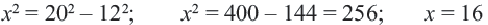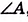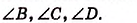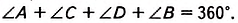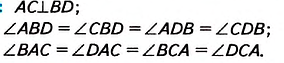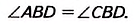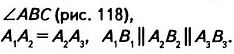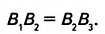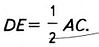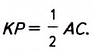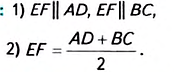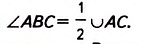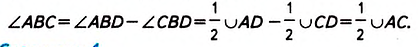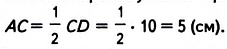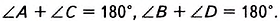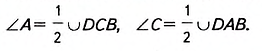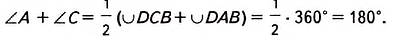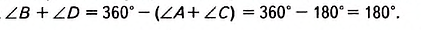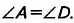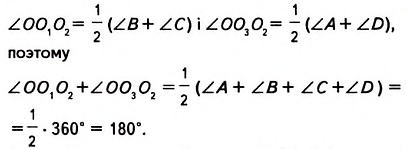- теория по математике 📈 планиметрия
- Выпуклый четырехугольник
- Виды и свойства выпуклых четырехугольников
- Прямоугольник
- Квадрат
- Параллелограмм
- Трапеция
- Виды трапеций
- Средняя линия трапеции
- Четырехугольник — виды и свойства с примерами решения
- Внутренние и внешние углы четырехугольника
- Сумма внутренних углов выпуклого четырёхугольника
- Сумма внешних углов выпуклого четырёхугольника
- Параллелограмм
- Параллелограмм и его свойства
- Признаки параллелограмма
- Прямоугольник
- Признак прямоугольника
- Ромб и квадрат
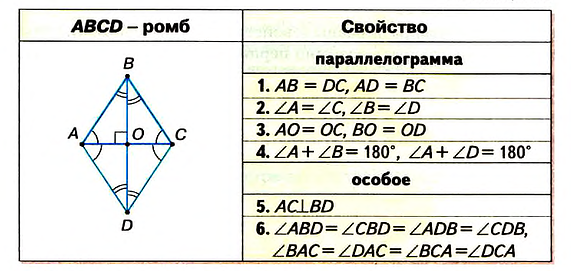
- Свойства ромба
- Трапеция
- Средняя линия треугольника
- Средняя линия трапеции
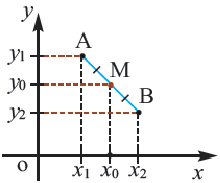
- Координаты середины отрезка
- Теорема Пифагора
- Справочный материал по четырёхугольнику
- Пример №1
- Признаки параллелограмма
- Пример №2 (признак параллелограмма).
- Прямоугольник
- Пример №3 (признак прямоугольника).
- Ромб. Квадрат
- Пример №4 (признак ромба)
- Теорема Фалеса. Средняя линия треугольника
- Пример №5
- Пример №6
- Трапеция
- Пример №7 (свойство равнобедренной трапеции).
- Центральные и вписанные углы
- Пример №8
- Вписанные и описанные четырёхугольники
- Пример №9
- Пример №10
- math4school.ru
- Четырёхугольники
- Основные определения и свойства
- Описанные четырёхугольники
- Вписанные четырёхугольники
- Параллелограмм
- Прямоугольник
- Квадрат
- Трапеция
- Дельтоид
- Ортодиагональные четырёхугольники
- 💥 Видео
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
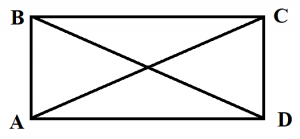
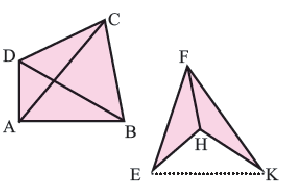
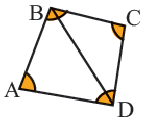
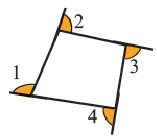
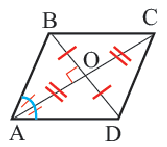
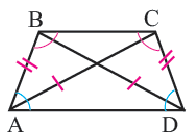
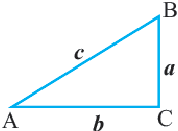
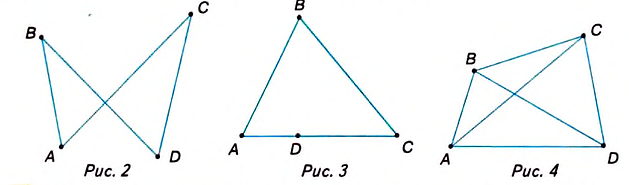
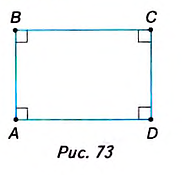
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

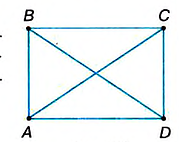
Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
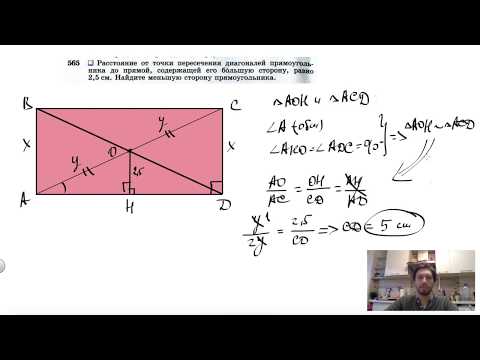
Видео:№565. Расстояние от точки пересечения диагоналей прямоугольника до прямойСкачать
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
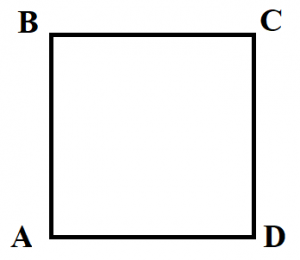
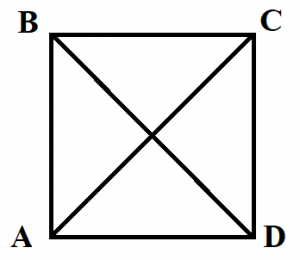
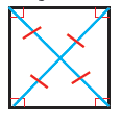
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
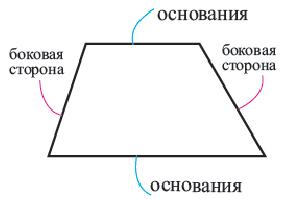
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
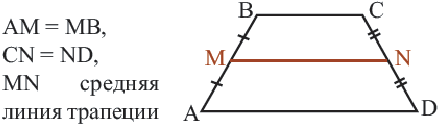
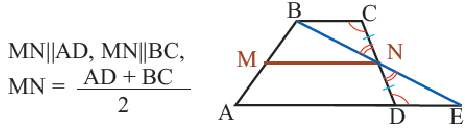
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

Четырехугольник — виды и свойства с примерами решения
Содержание:
Четырёхугольник — это фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом, никакие три из указанных точек не должны быть расположены на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки — сторонами четырёхугольника.
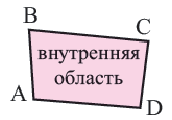
Вершины, являющиеся концами одной стороны четырёхугольника, называются соседними, а вершины, не принадлежащие одной стороне — противолежащими. Стороны, имеющие общую вершину, называются соседними сторонами, а не имеющие общих вершин — противолежащими сторонами. Отрезки, соединяющие противолежащие вершины, называются диагоналями четырёхугольника. Точки, принадлежащие четырёхугольнику, делят плоскость q на два множества, которые образуют две области — внутреннюю и внешнюю.
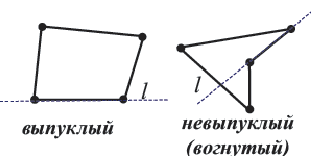
Четырёхугольник называется выпуклым, если все точки, принадлежащие внутренней области, находятся в одной полуплоскости от линии, содержащей любую сторону четырёхугольника, если эти точки находятся в разных полуплоскостях, то четырёхугольник называется невыпуклым (вогнутым).
Если соединить любые две точки внутренней области выпуклого многоугольника, то отрезок, соединяющий эти точки, целиком находится во внутренней области четырёхугольника.
Диагонали выпуклого четырёхугольника находятся во внутренней области. У невыпуклого четырёхугольника одна из диагоналей находится во внешней области. Каждая из двух диагоналей выпуклого четырёхугольника делит его на два треугольника.
Видео:Как найти отрезок, проходящий через точку пересечения диагоналей трапеции параллельно её основаниям?Скачать

Внутренние и внешние углы четырехугольника
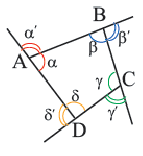
Угол, смежный любому углу выпуклого четырёхугольника, называется внешним углом. Из любой вершины четырёхугольника можно провести два внешних угла, которые являются вертикальными углами и соответственно равны друг другу. Поэтому, говоря о внешнем угле четырёхугольника, мы будем иметь в виду, один из них. На рисунке для внутренних углов 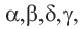
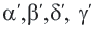
Каждый внутренний угол выпуклого четырёхугольника меньше 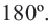
Сумма внутренних углов выпуклого четырёхугольника
Теорема. Сумма внутренних углов выпуклого четырёхугольника равна
Докажите теорему, основываясь на том, что сумма внутренних углов треугольника равна 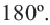
Сумма внешних углов выпуклого четырёхугольника
Теорема. Сумма внешних углов выпуклого четырёхугольника равна
Докажите теорему, опираясь на то, что внешний и внутренний угол, при каждой вершине являются смежными углами.
Параллелограмм
Параллелограмм и его свойства
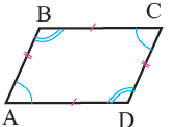
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Теорема 1. Противоположные стороны параллелограмма конгруэнтны.
Теорема 2. Противоположные углы параллелограмма конгруэнтны.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма равна
Теорема 4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
Теорема 5. Диагонали параллелограмма делят его на два конгруэнтных треугольника.
Признаки параллелограмма
Теорема 1. Четырёхугольник у которого две противоположные стороны конгруэнтный параллельны есть параллелограмм.
Теорема 2. Четырёхугольник с попарно конгруэнтными сторонами есть параллелограмм.
Теорема 3. Если диагонали четырёхугольника пересекаются и в точке пересечения делятся по полам, то этот четырёхугольник есть параллелограмм.
Прямоугольник
Параллелограмм, все углы которого прямые, называется прямоугольником.
Все свойства параллелограмма относятся к прямоугольнику.
Наряду с этим прямоугольник имеет следующее свойство:
Теорема. Диагонали прямоугольника конгруэнтны.
Признак прямоугольника
Параллелограмм, у которого диагонали конгруэнтны есть прямоугольник.
Ромб и квадрат
Свойства ромба
Параллелограмм, у которого все стороны конгруэнтны, называется ромбом. Все свойства параллелограмма относятся к ромбу. Наряду с этим, ромб обладает следующими свойствами:
Теорема 1. Диагонали ромба являются биссектрисами его углов и пересекаются под прямым утлом.
Теорема 2. (Обратная георема). Параллелограмм, у которого диагонали перпендикулярны, есть ромб. Если 
Доказательство теоремы 1.
Дано: 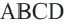
Докажите, что
Доказательство (словестное): По определению ромба 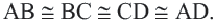
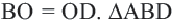
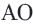
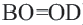
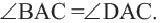
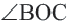
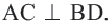
Если четырёхугольник является ромбом или квадратом, то справедливы следующие утверждения.
Ромб:
- 1. Все свойства параллелограмма действительны для ромба.
- 2. Все стороны конгруэнтны.
- 3. Диагонали взаимно перпендикулярны.
- 4. Диагонали ромба делят его углы пополам.
Квадрат:
- 1. Все свойства прямоугольника и ромба действительны для квадрата.
- 2. Все углы прямые.
- 3. Все стороны конгруэнтны.
- 4. Диагонали равны, взаимно перпендикулярны, делятся точкой пересечения пополам, являются биссектрисами углов квадрата.
Трапеция
Четырёхугольник, у которого только две стороны параллельны, называется трапецией.
Параллельные стороны трапеции называются основаниями, не параллельные стороны называются боковыми сторонами.
Трапеция, у которой боковые стороны равны называется равнобедренной трапецией.
Трапеция, у которой одна из боковых сторон перпендикулярна основанию называется прямоугольной трапецией.
Теорема 1. В равнобедренной трапеции углы, прилежащие к основанию конгруэнтны.
Теорема 2. Диагонали равнобедренной трапеции конгруэнтны.
План доказательства теоремы 2
Дано: 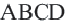
Докажите:
Средняя линия треугольника
Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне конгруэнтные отрезки, то они отсекают конгруэнтные отрезки и на другой его стороне. Если 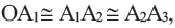
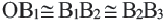
Доказательство: через точку 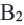
Если в условии теоремы Фалеса, вместо угла взять две произвольные прямые, то результат не изменится.
Исследование: 1) В треугольнике 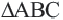
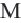
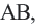
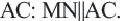
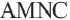
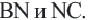
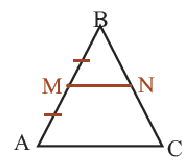
Определение: Отрезок, соединяющий середины двух сторон треугольника называется средней линией этого треугольника. Теорема. Средняя линия, соединяющая середины двух сторон треугольника, параллельна третьей стороне и равна ее половине
Доказательство. Пусть дан треугольник 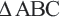
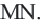
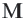
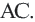
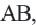
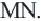
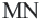
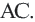
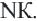
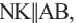

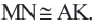
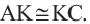
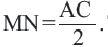
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющим середины боковых сторон трапеции.
Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство: Через точку 
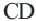
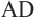
Координаты середины отрезка
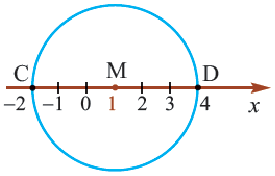
Исследование: Начертите числовую ось. Постройте окружность с центром в точке 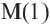
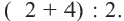
Координаты середины отрезка
1) Пусть на числовой оси заданы точки 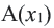
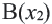
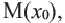
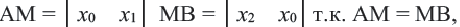
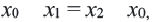
2) По теореме Фалеса, если точка 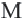
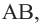
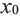
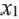
3) Координаты середины отрезка 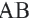
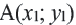
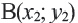
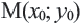
Убедитесь, что данная формула верна в случае, если отрезок 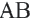
Теорема Пифагора
В этом разделе вы научитесь:
- различать рациональные и иррациональные числа;
- упрощать выражения, содержащие квадратные корни;
- решать задания на извлечение квадратного корня;
- основам теоремы Пифагора;
- решать практические задачи, применяя теорему Пифагора.
При решении таких задач как вычисления силы шторма на море, скорости автомобиля при аварии, определения места приземления при прыжке с парашютом часто приходится проводить вычисления с числами, стоящими под знаком корня.
Теорема Пифагора очень часто используется при решении геометрических задач.
Имя Пифагора ассоциируется с прямоугольным треугольником и соотношением между его сторонами. Греческий учёный Пифагор, живший в VI веке до нашей эры, является основателем школы, в которой преподавались музыка, гимнастика, философия и геометрия. Ученики школы называли себя Пифагорейцами. Они провозглашали гармонию музыки и чисел в природе и не верили в существование иррациональных чисел.
Практическая работа:
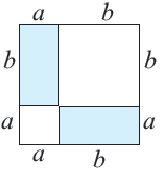
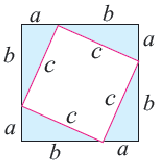
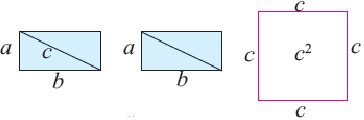
Шаг 1. Вырежьте из картона два одинаковых квадрата.
Шаг 2. На стороне одного из них отметьте отрезки 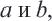
Шаг 3. Полученные фигуры расположите, как показано на рисунке.
Шаг 4. На сторонах другого квадрата отметьте отрезки 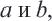
Шаг 5. Что вы можете сказать о конгруэнтности данных треугольников? К какому виду относится оставшаяся фигура, после того, как вы отрезали треугольники и убрали их? Чему равен каждый внутренний угол данного четырёхугольника?
Шаг 6. Расположите полученные фигуры, как показано на рисунке.
Шаг 7. Сравните результаты, которые вы получили на 3 и 6 шагах. К какому выводу вы пришли?
Теорема Пифагора:
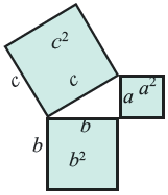
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Если рассмотреть площади квадратов, построенных на сторонах прямоугольного треугольника, то теорему Пифагора можно перефразировать так: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах:
Если в прямоугольном треугольнике заданы две стороны, то третью сторону можно найти по теореме Пифагора.
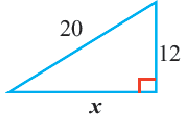
Пример:
Найдём длину катета на рисунке:
Историческая справка: Пифагор родился в 569 году до нашей эры на острове Самос в Греции. В истории его имя увековечено теоремой, которая называется теоремой Пифагора. Она известна своей простотой и практическим значением. Об этой теореме знали ещё задолго до Пифагора. Однако, из письменных источников следует, что впервые её доказал именно Пифагор. Помимо оригинального доказательства теоремы самим Пифагором, известны также доказательстве» Эвклида, Леонардо да Винчи, Президента Америки Джеймса Гарфилда. В 1940 году широкой публике была представлена книга, где приводилось 370 доказательств теоремы. На рисунке вы видите статую, возведённую в честь Пифагора на его родине на острове Самос.
Обратная теорема:
Если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным треугольником. Если 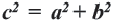
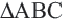
Прямоугольные треугольники, которых выражаются натуральными числами, называются Пифагоровыми треугольниками. Самый распространённый прямоугольный треугольник имеет стороны 3; 4; 5. Древние египтяне повсеместно пользовались этим треугольником для измерений. Такой треугольник называется Египетским треугольником. Треугольники со сторонами 5,12,13; 8,15,17; 7,24,25. также являются треугольниками Пифагора. А эти числа называются Пифагоровыми тройками. Если числа 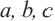
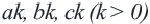
Видео:Задача о точке пересечения диагоналей трапецииСкачать

Справочный материал по четырёхугольнику
Обозначим четыре точки, например А, В, С, D, из которых никакие три не лежат на одной прямой. Последовательно соединим их непересекающимися отрезками АВ, ВС, CD, DA. Получим четырёхугольник ABCD.
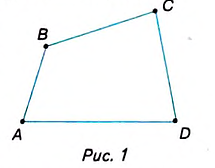
Точки А, В, С, D — вершины четырёхугольника, отрезки АВ, ВС, CD, DA — его стороны. Углы DAB, ABC, BCD, CDA — это углы четырёхугольника. Их также обозначают одной буквой —
Вершины, стороны и углы четырёхугольника называют его элементами. ? | Почему фигуры, изображённые на рисунках 2 и 3, не являются четырёхугольниками?
У фигуры на рисунке 2 отрезки АС и BD пересекаются, а у фигуры на рисунке 3 точки A, D, С лежат на одной прямой.
Четырёхугольник обозначают, последовательно записывая его вершины, начиная с любой из них. Например, четырёхугольник на рисунке 4 можно обозначить так: ABCD, или BCDA, или CDAB и т. д. Но для данного четырёхугольника запись, например, ADBC либо CDBA — неверна.
Две вершины, два угла или две стороны четырёхугольника могут быть либо соседними, либо противоположными. Например, в четырёхугольнике ABCD (рис. 4) вершины А и D, ZA и ZD, стороны AD и АВ — соседние, а вершины А и С, 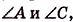
Отрезки, соединяющие противоположные вершины четырёхугольника, называются его диагоналями. На рис. 4 отрезки АС и BD — диагонали четырёхугольника ABCD.
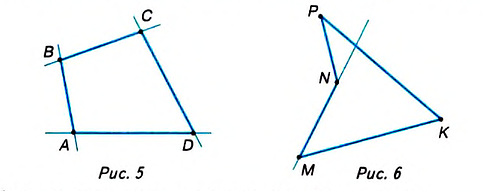
Четырёхугольники бывают выпуклыми и невыпуклыми.
Если четырёхугольник лежит по одну сторону от каждой прямой, соединяющей две его соседние вершины, то он выпуклый. На рисунке 5 четырёхугольник выпуклый, а на рисунке б — невыпуклый, поскольку он не лежит по одну сторону от прямой, проходящей через вершины М и N.
Мы будем изучать лишь выпуклые четырёхугольники. Сумма длин всех сторон четырёхугольника называется его периметром. Периметр обозначают буквой Р.
Записать, что периметр четырёхугольника ABCD равен 40 см, можно так: 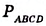
Пример:
Докажите, что каждая сторона четырёхугольника меньше суммы трёх других его сторон.
Решение:
Диагональ АС четырёхугольника ABCD делит его на два треугольника ABC и ADC (рис. 7). В 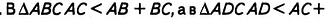
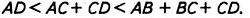
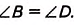
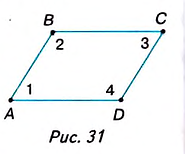
Может ли в параллелограмме быть только один острый угол? Не может, так как, согласно доказанной теореме, таких углов два.
Пример №1
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°. Докажите это.
Решение:
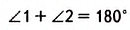
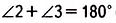
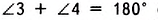
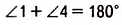
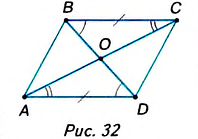
Теорема (свойство диагоналей параллелограмма).
Диагонали параллелограмма точкой их пересечения делятся пополам.
Дано: ABCD — параллелограмм (рис. 32), АС и BD — диагонали, О — точка пересечения диагоналей. Доказать: АО = ОС, ВО = OD.
Доказательство. 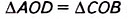
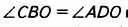
Для того чтобы доказать равенство отрезков (углов) в параллелограмме, докажите равенство треугольников, соответствующими элементами которых являются эти отрезки (углы).
Свойства параллелограмма приведены в таблице 3.
1. Возникает вопрос: Сколько данных необходимо для построения параллелограмма ?Таких данных должно быть три, среди которых — не более одного из его углов (один угол параллелограмма определяет остальные углы).
2. Название «параллелограмм» (parallelogrammon) происходит от сочетания греческих слов: «параллелос» — идущий рядом и «грамма» — линия.
Этот термин впервые упоминается в «Началах» Евклида (III в. до н. э.). Сначала вместо термина «параллелограмм» древнегреческий учёный использовал словосочетание «образованная параллельными линиями площадь» (часть плоскости, ограниченная двумя парами параллельных прямых).
Признаки параллелограмма
Решaя задачи, иногда требуется установить, что данный четырёхугольник — параллелограмм. Для этого используют признаки параллелограмма.
Теорема (признак параллелограмма).
Если противоположные стороны четырёхугольника попарнo равны, то такой четырёхугольник — параллелограмм.
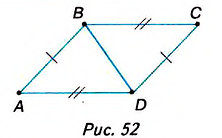
Дано: ABCD — четырёхугольник (рис. 52), АВ = DC, ВС = AD.
Доказать: ABCD— параллелограмм.
Доказательство. Проведём диагональ BD (рис. 52). 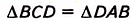

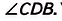
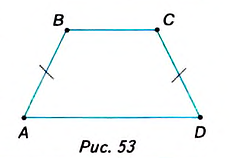
Можно ли считать четырёхугольник параллелограммом, если в нём две противоположные стороны равны, а две другие — параллельны?
Нет, нельзя. На рисунке 53 АВ = CD, ВС || AD, но четырёхугольник ABCD — не параллелограмм.
Теорема (признак параллелограмма).
Если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник — параллелограмм.
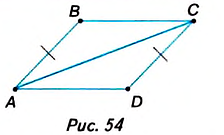
Дано: ABCD — четырёхугольник (рис. 54), и АВ = DC, АВ || DC.
Доказать: ABCD — параллелограмм.
Доказательство. Проведём диагональ АС (рис. 54). 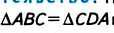
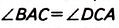
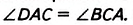
Пример №2 (признак параллелограмма).
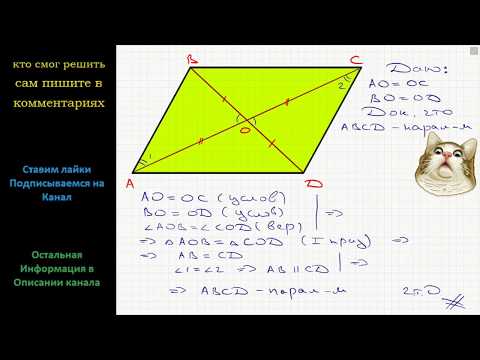
Если диагонали четырёхугольника делятся точкой их пересечения пополам, то такой четырёхугольник — параллелограмм. Докажите это.
Решение:
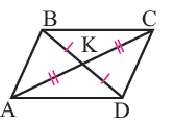
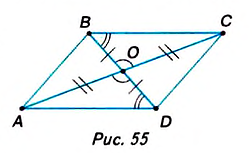
Пусть ABCD—данный четырёхугольник, О — точка пересечения его диагоналей и ВО= OD, АО= ОС (рис. 55). Докажем, что ABCD — параллелограмм. 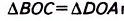
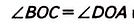
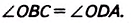
Поскольку в четырёхугольнике ABCD ВС= AD и ВС || AD, то, согласно доказанному признаку, этот четырёхугольник — параллелограмм.
Чтобы установить, что четырёхугольник — параллелограмм, докажите, что в нём:
- либо противоположные стороны попарно параллельны (определение параллелограмма),
- либо противоположные стороны попарно равны (признак),
- либо две противоположные стороны равны и параллельны (признак),
- либо диагонали делятся точкой их пересечения пополам (признак).
Вам уже знакомы понятия «необходимо», «достаточно», «необходимо и достаточно». В таблице 5 рассмотрите пары утверждений А и В и выясните смысл этих понятий.
Обратите внимание, что утверждения «Л достаточно для в» и «А необходимо для В» — взаимно обратные. Их можно объединить и сформулировать следующим образом.
Для того чтобы четырехугольник был параллелограммом, необходимо и достаточно, чтобы его противоположные стороны были попарно равны.
Иногда вместо «необходимое и достаточное условие» говорят «необходимый и достаточный признак», а чаще — просто «признак». Поэтому теоремы этого параграфа называем «признаками параллелограмма».
Прямоугольник
Параллелограммы, как и —у треугольники, можно разделить на виды. Прямоугольник — один из видов параллелограмма. На рисунке 73 вы видите параллелограмм ABCD являющийся прямоугольником. Дайте определение прямоугольнику и сравните его с приведённым в учебнике.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Поскольку прямоугольник — частный вид параллелограмма, то ему присущи все свойства параллелограмма:
- противоположные стороны равны;
- противоположные углы равны;
- диагонали делятся точкой их пересечения пополам.
Кроме этих свойств прямоугольник имеет ещё и особое свойство.
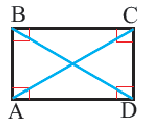
Дано: ABCD — прямоугольник, АС и BD — диагонали (рис. 74).
Доказать: АС = BD.
Доказательство. Прямоугольные треугольники ACDw DBA равны по двум катетам. При этом AD — общий катет, а катеты АВ и DC равны как противоположные стороны параллелограмма. Из равенства треугольников следует: АС = BD.
Свойства прямоугольника приведены в таблице 8.
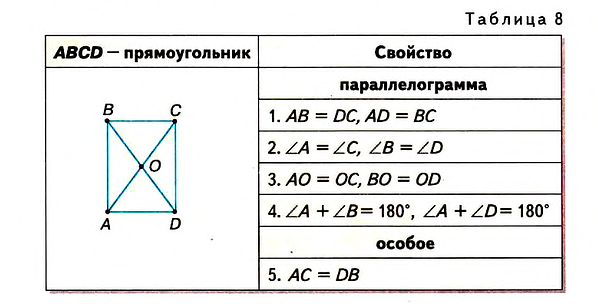
Пример №3 (признак прямоугольника).
Если диагонали параллелограмма равны, то такой параллелограмм — прямоугольник. Докажите это.
Решение:
Пусть ABCD — параллелограмм, в котором АС = BD (рис. в табл. 8). Докажем, что 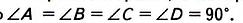
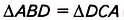
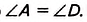
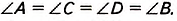
Следовательно, 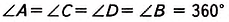
Для того чтобы установить, что данный параллелограмм — прямоугольник, докажите, что у него: либо все его углы прямые (определение прямоугольника), либо диагонали равны (признак).
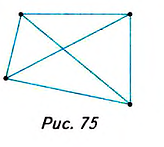
Можно ли утверждать, что четырёхугольник, в котором диагонали равны, — это прямоугольник? Нет, нельзя (см. рис. 75). Необходимо проверить, выполняется ли один из признаков параллелограмма. Например, делятся ли диагонали точкой их пересечения пополам.
Возникает вопрос: Можно ли сформулировать другие определения прямоугольника ?
В младших классах прямоугольником называли четырёхугольник, все углы в котором прямые. Теперь мы определили прямоугольник как частный вид параллелограмма. Возможны и такие определения прямоугольника: параллелограмм, в котором все углы равны (действительно, сумма углов параллелограмма составляет 360°, тогда каждый из них равен 90°); параллелограмм, в котором есть прямой угол (действительно, в параллелограмме сумма смежных углов составляет 180е, а противоположные углы равны. Если один из его углов прямой, то и три остальные — прямые). Эти определения прямоугольника эквивалентны.
Следовательно, существуют разные определения одного и того же понятия.
Ромб. Квадрат
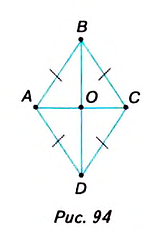
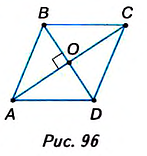
Могут ли в параллелограмме все стороны быть равными? Да, могут. На рисунке 94 в параллелограмме ABCD АВ = ВС = = CD = AD. Это ещё один вид параллелограмма — ромб.
Параллелограмм, у которого все стороны равны, называется ромбом.
Можно ли утверждать, что параллелограмм является ромбом, если две его смежные стороны равны? Да, можно. Равенство всех сторон такого параллелограмма следует из свойства: противоположные стороны параллелограмма равны.
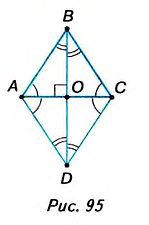
Теорема (свойства диагоналей ромба). Диагонали ромба взаимно перпендикулярны. Диагонали ромба делят его углы пополам.
Дано: ABCD — ромб (рис. 95), О— точка пересечения диагоналей АС и BD.
Доказать:
Доказательство. Согласно определению ромба АВ = ВС, поэтому треугольник ABC— равнобедренный. Так как ромб ABCD— параллелограмм, то АО — ОС. Отсюда ВО— медиана равнобедренного треугольника ABC, следовательно, высота и биссектриса этого треугольника. Поэтому 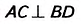
Аналогично доказываем, что диагональ BD делит пополам угол D, а диагональ АС— углы А и С ромба ABCD.
Свойства ромба приведены в таблице 10. Таблица 1 О
Пример №4 (признак ромба)
Докажите, что параллелограмм, диагонали которого взаимно перпендикулярны, является ромбом.
Решение:
Пусть ABCD — данный параллелограмм, в котором 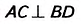
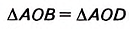
Так как ромб — это частный вид параллелограмма, то он имеет все свойства параллелограмма (назовите их). Кроме того, ромб обладает особыми свойствами. У них сторона АО — общая, OB = OD по свойству диагоналей параллелограмма, 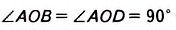
Для того чтобы установить, что данный параллелограмм — ромб, докажите, что в нем:
- либо все стороны равны (определение ромба),
- либо диагонали взаимно перпендикулярны (признак).
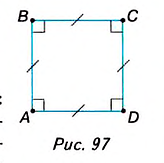
Прямоугольник, в котором все стороны равны, называется квадратом.
На рисунке 97 вы видите квадрат ABCD.
Существуют и другие определения квадрата: ромб, в котором все углы прямые, называется квадратом; прямоугольник, в котором все стороны равны, называется квадратом; параллелограмм, в котором все стороны равны и все углы прямые, называется квадратом. Следовательно, квадрат имеет все свойства параллелограмма, прямоугольника и ромба. Перечислим свойства квадрата.
- Противоположные стороны и противоположные углы квадрата равны. Диагонали квадрата в точке пересечения делятся пополам (свойства параллелограмма).
- Диагонали квадрата равны (свойство прямоугольника).
- Диагонали квадрата взаимно перпендикулярны и делят его углы пополам (свойства ромба).
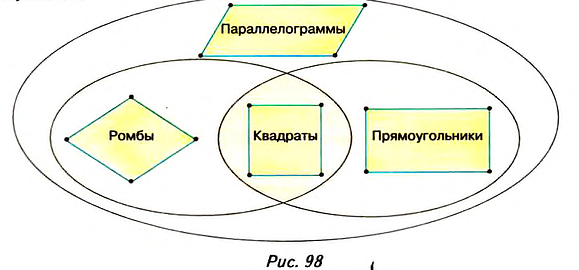
Квадрат является частным видом и ромба, и прямоугольника, и параллелограмма. Ромб и прямоугольник — это частные виды параллелограмма. Соотношение между видами параллелограммов показано на
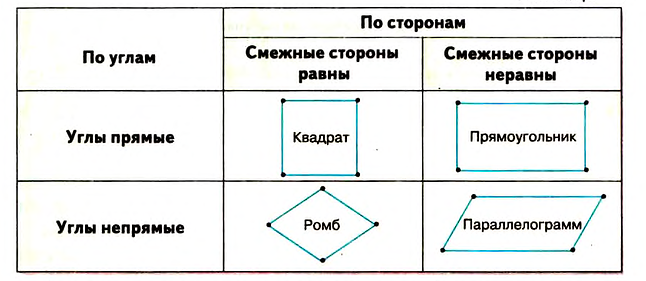
1. Рассмотрите таблицу классификации параллелограммов по соседним углам и смежным сторонам. Предложите собственную классификацию изученных видов параллелограмма.
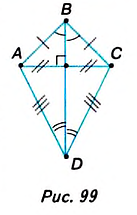
2. Кроме параллелограммов есть ещё один вид четырёхугольников — дельтоид. Эту фигуру получим, если два равнобедренных треугольника ABC и ADCc равными основаниями АС приложить друг к другу так, как показано на рисунке 99.
Свойства дельтоида следуют из свойств равнобедренного треугольника. Например, диагонали взаимно перпендикулярны, одна из них делит углы пополам и другую диагональ — пополам. Сформулируйте, пользуясь рисунком, другие свойства дельтоида. Если равнобедренные треугольники, из которых образован дельтоид, равны, то такой дельтоид является ромбом. Если равнобедренные треугольники к тому же прямоугольные, то дельтоид является квадратом.
3. Слово «ромб» происходит от греческого rhombos — юла, вращение. Слово «квадрат» происходит от латинского quadratum — четырёхугольник. Квадрат был первым четырёхугольником, который рассматривался в геометрии.
Теорема Фалеса. Средняя линия треугольника
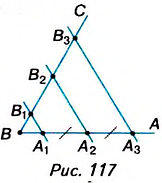
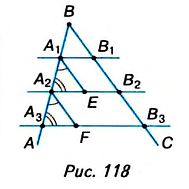
Начертите угол ABC (рис. 117).
Произвольным раствором циркуля отложите на стороне АВ угла равные отрезки 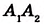
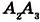
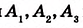
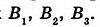
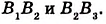
Теорема Фалёса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Дано:
Доказать:
Доказательство. Проведём через точки 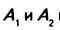
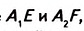
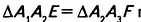
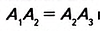
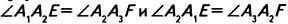

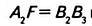
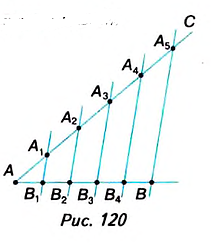
Справедлива ли теорема Фалеса, если вместо сторон угла взять две произвольные прямые? Да, справедлива. Параллельные прямые, пересекающие две заданные прямые и отсекающие на одной прямой равные отрезки, отсекают равные отрезки и на другой прямой (рис. 119).
Пример №5
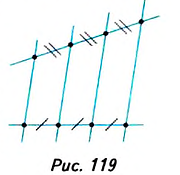
Разделите данный отрезок АВ на пять равных частей.
Решение:
Проведём из точки А луч АС, не лежащий на прямой АВ (рис. 120).
Отложим на луче АС пять равных отрезков: АА,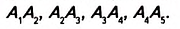
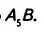
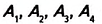
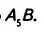
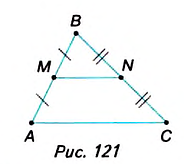
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
На рисунке 121 отрезок MN — средняя линия 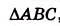
Теорема (свойства средней линии треугольника). Средняя линия треугольника параллельна третьей его стороне и равна её половине.
Дано: 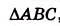
Доказать:
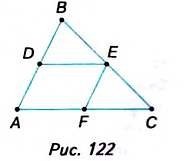
Доказательство. 1) Пусть DE- средняя линия 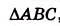
2) Проведём прямую EF|| АВ. По теореме Фалеса, прямая EFделит отрезок 1
АС пополам: 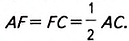
Пример №6
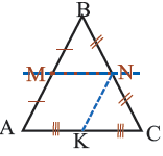
Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма.
Решение:
Пусть ABC— данный четырёхугольник и М, N, Р, К — середины его сторон (рис. 123). Докажем, что MNPK — параллелограмм. Проведём диагональ AC. MN— средняя линия ААВС.
Поэтому 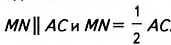
Получаем: MN || АС и КР || АС, отсюда MN || КР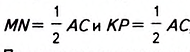
Если по условию задачи даны середины некоторых отрезков, то можно использовать свойства средней линии треугольника.
Древнегреческого учёного Фалеса из Милета (625 — 548 гг. до н. э.) считают одним из семи мудрецов мира. Гений Фалеса нашёл воплощение в разных сферах деятельности. Он занимался инженерным делом, был государственным деятелем, математиком, астрономом. Особой заслугой Фалеса является то, что он ввёл в математику идею доказательства. Учёный доказал, что углы при основании равнобедренного треугольника равны, что диаметр делит окружность на две равные части, что прямой угол можно вписать в полуокружность и т. д. Историки полагают, что именно Фалес начал использовать основные геометрические инструменты — циркуль и линейку. Учёный измерял высоту египетских пирамид по длине их теней, впервые предсказал солнечное затемнение, наблюдавшееся в 585 г. до н. э.
Трапеция
Вы уже знаете, что четырёхугольник с попарно параллельными противоположными сторонами — параллелограмм.
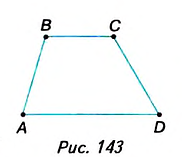
На рисунке 143 изображён четырёхугольник ABCD, две стороны AD и ВС которого параллельны, а две другие — АВ и CD — непараллельны. Такой четырёхугольник — трапеция. Дайте определение трапеции и сравните его с приведённым в учебнике.
Трапецией называется четырёхугольник, в которомдве стороны параллельны, а две другие — непараллельны.
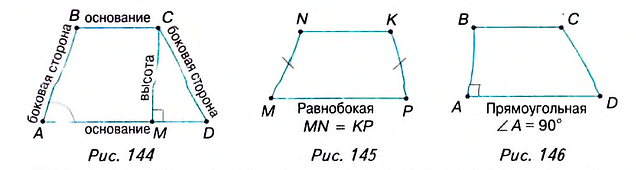
Параллельные стороны трапеции называются её основаниями, а непараллельные — боковыми сторонами. На рисунке 144 AD и ВС — основания трапеции, АВ и CD — боковые стороны.
Могут ли основания трапеции быть равными? Не могут, поскольку тогда получим параллелограмм.
Высотой трапеции называется перпендикуляр, проведённый из любой точки одного основания к другому основанию либо его продолжению (рис. 144).
Трапеция, в которой боковые стороны равны, называется равнобедренной. На рисунке 145 трапеция MNKP — равнобедренная, поскольку MN = КР.
Трапецию, один из углов которой прямой, называют прямоугольной. Трапеция ABCD (рис. 146) — прямоугольная, поскольку 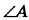
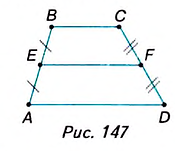
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
На рисунке 147 отрезок EF — средняя линия трапеции ABCD, так как точки Е и F — середины боковых сторон АВ и CD.
Теорема (свойства средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
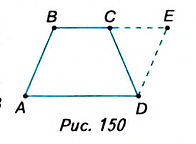
Дано: ABCD — трапеция с основаниями AD и ВС (рис. 148), EF— средняя линия. Доказать:
Доказательство. Поскольку EF — средняя линия трапеции ABCD, то АЕ= BE, DF= CF. Через точки В и проведём прямую, пересекающую продолжение основания ADb точке Q. 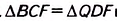
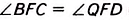
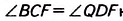
1) По свойству средней линии треугольника EF || АО, поэтому EF || AD. Поскольку AD || ВС, то EF\ ВС.
Пример №7 (свойство равнобедренной трапеции).
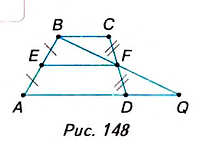
В равнобедренной трапеции углы при основании равны. Докажите это.
Решение:
Пусть в трапеции ABCD (рис. 149) АВ = CD. Докажем, что углы при основании AD равны.
Проведём СЕ || АВ. Полученный четырёхугольник АВСЕ— параллелограмм, так как его противоположные стороны попарно параллельны. По свойству параллелограмма, АВ = СЕ, а по условию — АВ = CD. Следовательно, С£= CD и 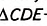

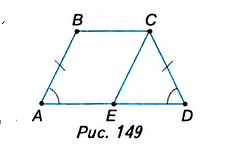
Если в условии задачи дана трапеция, то полезно такое дополнительное построение: проведите через вершину трапеции прямую, параллельную боковой стороне (рис. 149 или 150), и используйте свойства полученных параллелограмма и треугольника.
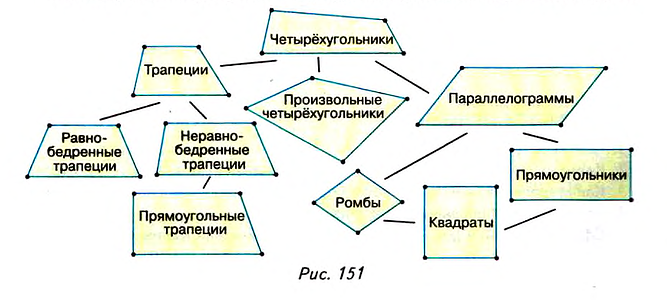
Решите предыдущую задачу, используя рисунок 150. Посмотрите на рисунок 151, где изображены изученные вами
Центральные и вписанные углы
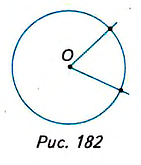
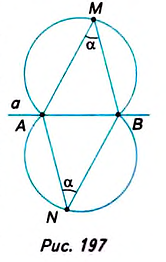
Проведём окружность с центром О и построим угол с вершиной в центре окружности (рис. 182). Получили центральный угол в окружности.
Угол с вершиной в центре окружности называется центральным углом.
Теорема (о вписанном угле). Вписанный угол измеряется половиной дуги, на которую он опирается.
Дано: 
Доказать:
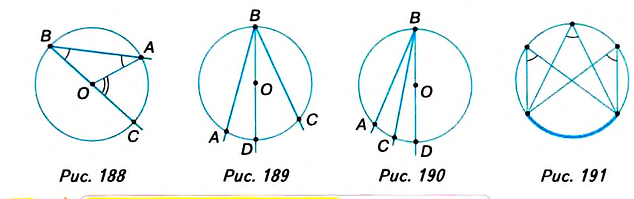
Доказательство. Рассмотрим три случая расположения центра , окружности относительно сторон данного вписанного угла.
1. Центр окружности лежит на стороне вписанного угла (рис. 188). Проведём отрезок ОД тогда центральный угол АОС является внешним углом 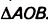

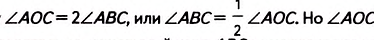
2. Центр окружности лежит во внутренней области вписанного угла (рис. 189). Проведём луч ВО, тогда данный угол равен сумме двух углов:
Из доказанного в первом случае следует, что 

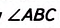
3. Центр круга лежит во внешней области вписанного угла (рис. 190). Проведём луч ВО, тогда:
Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 191). Действительно, каждый из них измеряется половиной одной и той же дуги.
Следствие 2.
Вписанный угол, опирающийся на диаметр, — прямой (рис. 192). Действительно, такой угол измеряется половиной полуокружности, то есть 180°: 2 = 90°.
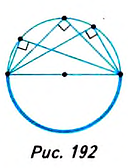
Равны ли вписанные углы, опирающиеся на равные дуги (рис. 193)? Да, так как каждый из этих углов измеряется половиной равных дуг, градусные меры которых равны.
Пример №8
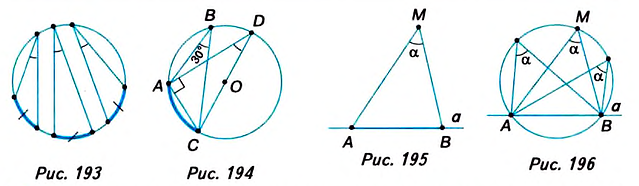
Хорды окружности АВ и ВС образуют угол 30°. Найдите хорду АС, если диаметр окружности равен 10 см.
Решение:
Проведём диаметр CD и соединим точки A и D (рис. 194). 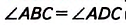
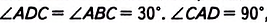
Для того чтобы доказать равенство двух углов, покажите, что они являются вписанными в одну окружность и опираются на одну и ту же дугу либо на равные дуги данной окружности.
Рассмотрим геометрическое место точек, которое используется при решении сложных задач на построение.
Пусть АВ — некоторый отрезок прямой а, М— произвольная точка, не лежащая на прямой a, 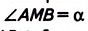
Если описать окружность около 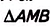
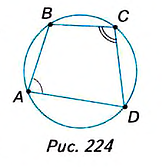
Вписанные и описанные четырёхугольники
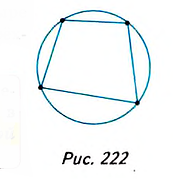
Отметим на окружности четыре точки и соединим их хордами (рис. 222). Получили четырёхугольник, вписанный в окружность.
Четырёхугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность — описанной около этого четырехугольника.
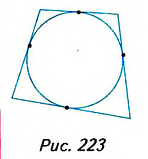
Отметим на окружности четыре точки и проведём через них отрезки касательных, как показано на рисунке 223. Получили четырёхугольник, описанный около окружности.
Четырёхугольнику все стороны которого касаются окружности, называется описанным около этой окружности, а окружность — вписанной в этот четырёхугольник.
Свойство вписанного четырёхугольника и его признак связаны с углами этого четырёхугольника.
Теорема (свойство углов вписанного четырёхугольника). Сумма противоположных углов вписанного четырёхугольника равна 180″.
Дано: четырёхугольник ABCD, вписанный в окружность (рис. 224).
Доказать:
Доказательство. Углы А, В, Си D вписаны в окружность.
Из теоремы о вписанном угле следует:
Тогда
Сумма всех углов четырёхугольника равна 360°, а сумма углов А и С — 180°. Тогда
Около каждого ли четырёхугольника можно описать окружность? В отличие от треугольника не каждый четырёхугольник — вписанный. Приведём признак вписанного четырёхугольника без доказательства.
Теорема (признак вписанного четырёхугольника). Если в четырёхугольнике сумма двух противоположных углов равна 180е, то около такого четырёхугольника можно описать окружность.
Пример №9
Докажите, что около равнобедренной трапеции можно описать окружность.
Решение:
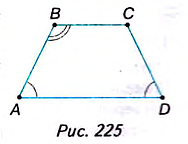
Пусть ABCD — равнобедренная трапеция с основаниями AD и ВС (рис. 225).
Докажем, что 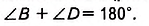
Поэтому, 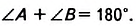
Тогда 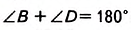
Теорема (свойство сторон описанного четырёхугольника). Суммы противоположных сторон описанного четырёхугольника равны.
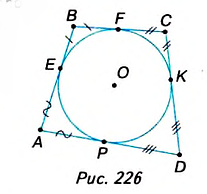
Дано: четырёхугольник ABCD, описанный около окружности (рис. 226), Е, F, K и P — точки касания.
Доказать: АВ + CD = ВС + AD.
Доказательство. По свойству касательных, проведённых к окружности из одной точки: АЕ = АР; BE = BF, СК = CF, DK = DP. Сложив почленно эти равенства, получим: АЕ + BE + СК + DK = АР + BF + CF + DP, то есть АВ + CD = ВС + AD.
В каждый ли четырёхугольник можно вписать окружность? В отличие от треугольника, не в каждый четырёхугольник можно вписать окружность. Приведём признак описанного четырёхугольника без доказательства.
Теорема (признак описанного четырёхугольника). Если в четырёхугольнике суммы противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
Чтобы доказать, что четырёхугольник MNKP (рис. 227) — вписанный, покажите, что: либо ے M + ے K = 180°, либо ے N + ے P= 180°. Чтобы доказать, что четырёхугольник ABCD (рис. 227) — описанный, покажите, что: AB + CD = AD + BC.
1. Кроме окружностей, вписанной и описанной около четырёхугольника, существуют ещё и вневписанные окружности.
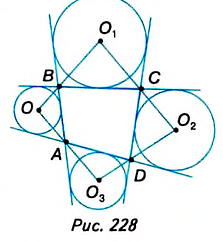
Проведём в произвольном четырёхугольнике ABCD биссектрисы внешних углов при вершинах А, В, С и D [рис. 228). Точки их пересечения 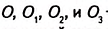
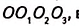
Следовательно, четырёхугольник 
2. Древнегреческие учёные открыли, кроме уже известных вам, другие интересные свойства вписанных и описанных четырёхугольников. Например.
Теорема Птолемея (II в.). Произведение диагоналей вписанного четырёхугольника равно сумме произведений его противоположных сторон.
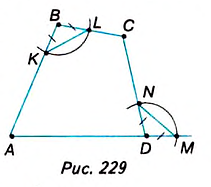
Задача Архимеда (III в. до н. э.). Если диагонали вписанного четырёхугольника перпендикулярны, то сумма квадратов четырёх отрезков, на которые делятся диагонали точкой пересечения, равна квадрату диаметра описанной окружности. Позднее (IX — XIII в.) арабские учёные дополнили сведения о вписанных и описанных четырёхугольниках и способах исследования их свойств. Так, одарённый геометр Гасан ибн-Гайтем (умер в 1038 г.) предложил, способ, позволяющий установить, используя лишь циркуль, является ли данный четырёхугольник вписанным. Пусть дан четырёхугольник ABCD(рис. 229).
Продолжим сторону AD за точку D. Проведём дуги равных окружностей с центрами в точках В и D. Если KL = МО, то четырёхугольник ABCD — вписанный, так как ے ABC + ے ADC = 180° (докажите это). В иных случаях четырёхугольник не является вписанным.
4 | 3. При решении задач иногда рассматриваются окружности, не заданные в условии. На рисунке к задаче сначала находим четырёхугольник, около которого можно описать окружность либо в который можно вписать окружность, а потом используем свойства хорд, диаметров, вписанных углов, углов с вершиной внутри окружности и т. д.
Пример №10
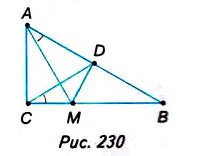
Из произвольной точки М катета ВС прямоугольного треугольника ABC проведён перпендикуляр MD к гипотенузе АВ (рис. 230). Докажем, что ے MAD= ے MCD.
Решение:
Около четырёхугольника ADMC можно описать окружность, так как ے ACM+ ے ADM= 180°.
Тогда ے MAD= ے MCD— вписанные углы, опирающиеся на одну дугу MD.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:№120. Через точку О пересечения диагоналей квадрата со стороной а проведена прямая ОКСкачать

math4school.ru
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Четырёхугольники
Видео:№128. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямаяСкачать

Основные определения и свойства

Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
Сумма углов выпуклого четырёхугольника равна 360°:
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:
Площадь произвольного выпуклого четырёхугольника равна:

Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.
Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.
Площадь произвольного выпуклого четырёхугольника:



Если M , N , P , Q – середины сторон выпуклого четырёхугольника ABCD , а R , S – середины его диагоналей, то четырёхугольники MNPQ , MRPS , NSQR являются параллелограммами и называются параллелограммами Вариньона.
Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD . Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;

Отрезки MP , NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника.
В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки.
Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам:
MG=GP , NG=GQ , RG=GS .
Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:
MP 2 + NQ 2 + RS 2 = ¼ (AB 2 +BC 2 +CD 2 +AD 2 +AC 2 +BD 2 ).
Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь:

Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Описанные четырёхугольники

Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной.
Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны:
Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:
Площадь описанного четырёхугольника:
где r – радиус вписанной окружности, p – полупериметр четырёхугольника.
Площадь описанного четырёхугольника:

Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:
AK = AN , BK = BL , CL = CM , DM = DN .
Если O – центр окружности, вписанной в четырёхугольник ABCD, то
∠AOB+∠COD = ∠BOC+∠AOD =180°.
Для описанного четырёхугольника ABCD со сторонами AB = a , BC = b , CD = c и AD = d верны соотношения:
Видео:Доказательство замечательного свойства трапеции при помощи метода параллельной проекцииСкачать

Вписанные четырёхугольники

Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника.
Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°:
Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Радиус окружности, описанной около четырёхугольника:
Площадь вписанного четырёхугольника:

Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.
Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.
У вписанного четырёхугольника любые два связанных угла равны.

Если четырёхугольник одновременно является описанным и вписанным, то его площадь:
Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:
Видео:Свойства диагоналей прямоугольника. Свойства диагоналей квадрата | Математика 4 класс #9 | ИнфоурокСкачать

Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:
У параллелограмма противолежащие стороны равны и противолежащие углы равны:
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A +∠ B =∠ B +∠ C =∠ C +∠ D =∠ A +∠ D =180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:
Каждая диагональ делит параллелограмм на два равных треугольника:
∠ ABC =∠ CDA ; ∠ ABD =∠ CDB .
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e 2 +f 2 = a 2 +b 2 +a 2 +b 2 = 2(a 2 +b 2 ).
- Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник – параллелограмм.
- Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
- Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм.
- Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.

Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне:
Площадь параллелограмма можно определить:
- через его сторону и высоту, проведённую к ней:
- через две его стороны и угол между ними:

Ромбом называется параллелограмм, у которого все стороны равны:
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:
∠ ABD =∠ CBD =∠ ADB =∠ CDB ; ∠ BAC =∠ DAC =∠ BCA =∠ DCA .

В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей.
Радиус окружности, вписанной в ромб, можно вычислить:
- через диагонали ромба и сторону:
- через отрезки, на которые делит сторону ромба точка касания:
Площадь ромба можно определить:
- через сторону и угол ромба:
- через сторону и радиус вписанной окружности:
Видео:8 класс, 4 урок, ПараллелограммСкачать

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые:

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:
Площадь прямоугольника можно определить:
- через диагонали и угол между ними:

Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали:
Видео:Геометрия Признак параллелограмма: Если в четырехугольнике диагонали точкой пересечения делятсяСкачать
Квадрат

Квадрат – это прямоугольник, у которого все стороны равны:

Диагонали квадрата равны и перпендикулярны.
Сторона и диагональ квадрата связаны соотношениями:

У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.
Радиус описанной окружности:
Радиус вписанной окружности:
Видео:Диагонали трапеции и точка их пересеченияСкачать

Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:
Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.

Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:
Средняя линия трапеции параллельна её основаниям и равна их полусумме:

При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ:
Δ AED ∼ Δ BEC , k = AD / BC .
Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ:
Δ AОD ∼ Δ CОВ , k = AD / BC .
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:

Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон:
Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон:
Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств:
Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом:
Радиус вписанной в трапецию окружности можно определить:
- через отрезки, на которые делится боковая сторона точкой касания:

Равнобокой называется трапеция, у которой боковые стороны равны:
У равнобокой трапеции:
- углы при основании равны:
- сумма противолежащих углов равна 180?:
Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Стороны и диагональ равнобокой трапеции связаны соотношением:

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

Площадь трапеции можно определить:
- через полусумму оснований (первую среднюю линию) и высоту:
- через диагонали и угол между ними:
Видео:№434. Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон.Скачать

Дельтоид


Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон.
Дельтоид может быть выпуклым или невыпуклым.
Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом.
В любом дельтоиде углы между соседними неравными сторонами равны.
Площадь любого дельтоида можно определить:
- через две соседние неравные стороны и угол между ними:


В любой выпуклый дельтоид можно вписать окружность.
Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида.
Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.

Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°.
Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
Видео:14. Свойства диагоналей прямоугольника и квадрата.Скачать

Ортодиагональные четырёхугольники

Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом.
Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
- для сторон четырёхугольника верно: a²+c² = b²+d ²;
- для площади четырёхугольника верно: S = ½ef ;
- параллелограмм Вариньона с вершинами в серединах сторон четырёхугольника является прямоугольником.

Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности:

Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны:
Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О , то верны соотношения:
💥 Видео
Свойства диагоналей #какзапомнить #свойствадиагоналей #четырехугольникиСкачать

Свойства диагоналей прямоугольника. Геометрия 8 класс. Тесты. Четырехугольники. Математика.Скачать

№442. Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.Скачать
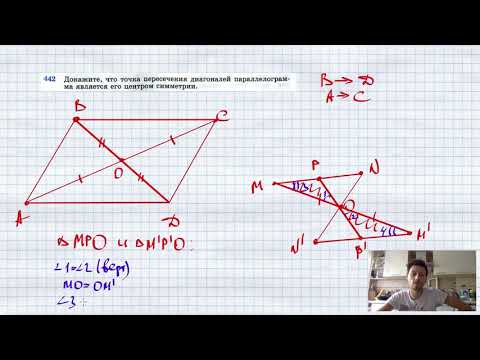
Свойства диагоналей параллелограмма | Геометрия 8-9 классыСкачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать