Точка м лежит вне плоскости четырехугольника abcd плоскости mab и mbc пересекаются по прямой

Вопрос по алгебре:

1. Плоскость, притом только одна, проходит через а) две пересекающиеся прямые; б) одну прямую; в) две скрещивающиеся прямые.

2. Точка М лежит вне плоскости четырехугольника АВСД. Плоскости МАВ и МВС пересекаются по прямой
. М а) МА;
А В б) МВ;
в) МС;
г) АВ.

3. Точки А, В, С и Д не лежат в одной плоскости, следовательно
а) какие-то три из них лежат на одной прямой;
б) никакие из трех данных точек не лежат на одной прямой;
в) прямые АВ и СД пересекаются.

4. Точки А, В, С лежат на одной прямой, точка D не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных
плоскостей при этом получилось?
а) 2; б) 3; в) 1; г) бесконечно много.

5. Назовите общую прямую плоскостей AFD и DEF.
а) AD; б) DE; в) DF; г) AF.

6. Прямая а лежит в плоскости α и пересекает плоскость β. Каково взаимное расположение плоскостей α и β?
а) они совпадают;
б) имеют только одну общую точку;
в) не пересекаются;
г) пересекаются по некоторой прямой.

7. Если через две параллельные прямые проходят пересекающиеся плоскости, то линия их пересечения
а) параллельна каждой из двух прямых или совпадает с одной из них;
б) пересекается хотя бы с одной из этих прямых;
в) скрещивается хотя бы с одной из прямых.

8. Выберите верное утверждение.
а) Две прямые называются параллельными, если они не имеют общих точек;
б) две прямые, параллельные третьей прямой, параллельны;
в) две прямые, перпендикулярные третьей прямой, параллельны;
г) если углы равны, то их стороны соответственно сонаправлены.

9. Через вершину А параллелограмма ABCD и точку М, не лежащую в плоскости параллелограмма, проведена прямая АМ. Чему равен угол между прямыми АМ и ВС, если угол MAD равен 120˚?
а) определить нельзя; б) 120˚; в) 30˚; г) 60˚; д) 150˚.

10. Точка К не лежит в плоскости треугольника ВДС, точки А, М, и Р – середины отрезков КВ, КД, КС соответственно. Каково взаимное расположение плоскостей ВДС и АМР ?
а) плоскости параллельны; б) плоскости пересекаются; в) их расположение определить нельзя.

11. В кубе АВСДА1В1С1Д1 точка Е лежит на ребре АА1, а точка К – на ребре АВ Точка пересечения прямой ЕК с плоскостью грани ВВ1С1С лежит на прямой а) ВС; б) В1С1; в) ВВ1; г) СС1.

12. Прямая а параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая а параллельна любой прямой, лежащей в плоскости α;
б) прямая а не пересекает ни одну прямую, лежащую в плоскости α;
в) прямая а скрещивается со всеми прямыми плоскости α;
г) прямая а имеет общую точку с плоскостью .

13. В треугольнике АВС точки F и E принадлежат сторонам СВ и АВ соответственно, причём ВЕ : ЕА = 2 : 3. Через эти точки провели плоскость, параллельную АС. Найдите отношение BF : FC.
а) 3 : 2; б) 2 : 3; в) 3 : 5; г) 2 : 5.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Видео:№131. В тетраэдре ABCD точка М — середина ребра ВС, АВ = AC, DB = DC. Докажите, что плоскостьСкачать

Точка М лежит вне плоскости четырехугольника АВСД?

Геометрия | 10 — 11 классы

Точка М лежит вне плоскости четырехугольника АВСД.

Плоскости МАВ и МВС пересекаются по прямой.

АВ. С тебя спасибо ГОООООО ЛАЙК.

Видео:№23. Точка М не лежит в плоскости прямоугольника ABCD.Скачать

Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости?

Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости.

Видео:№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать

Плоскости а и б пересекаются по прямой Т?

Плоскости а и б пересекаются по прямой Т.

Прямая А лежит в плоскости а и пересекает плоскость б.

Пересекаются ли прямые А и Т?

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Плоскости «альфа» и «бета»пересекаются по прямой а?

Плоскости «альфа» и «бета»пересекаются по прямой а.

Прямая b, лежащая в плоскости «бета», пересекает плоскость «альфа»в точке А.

Где лежит точка А?

Видео:№166. Неперпендикулярные плоскости α и β пересекаются по прямой MN. В плоскости βСкачать

Прямая а лежит в плоскости альфа?

Прямая а лежит в плоскости альфа.

Плоскость бета пересекает плоскость альфа по прямой б.

Известно, что прямая а пересекает плоскость бета в точке Б.

Где лежит точка Б?

Видео:№159. Прямая ВМ перпендикулярна к плоскости прямоугольника ABCD. ДокажитеСкачать

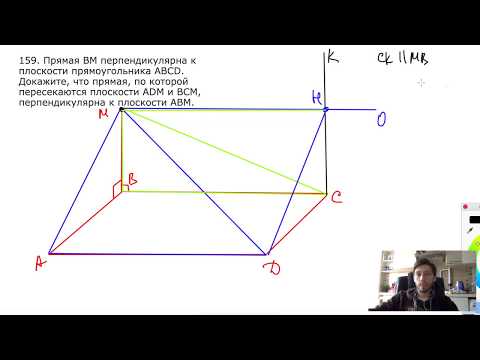
Прямая АМ перпендикулярна плоскости квадрата АВСД, диагонали которого пересекаются в точке О?

Прямая АМ перпендикулярна плоскости квадрата АВСД, диагонали которого пересекаются в точке О.

Докажите, что прямая ВD перпендикулярна плоскости АМО.

Видео:№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

Прямая а пересекает плоскость «а»?

Прямая а пересекает плоскость «а».

Лежит ли в плоскости «а» хоть одна прямая, параллельна «а»?

Видео:№24. Точка М не лежит в плоскости трапеции ABCD с основанием AD.Скачать

Прямая A лежит в плоскости альфа прямая b пересекает плоскость альфа в точке B не лежfщей на этой прямой A докажите что прямые A и B не пересекаются?

Прямая A лежит в плоскости альфа прямая b пересекает плоскость альфа в точке B не лежfщей на этой прямой A докажите что прямые A и B не пересекаются.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Плоскости a и b пересекаются по прямой р?

Плоскости a и b пересекаются по прямой р.

Точка А лежит в плоскости a вне прямой р.

Точка В лежит в плоскости b вне прямой р.

Как расположены прямые АВ и р?

Видео:№129. Прямая AM перпендикулярна к плоскости квадрата ABCD, диагонали которого пересекаютсяСкачать

Доказать, что все прямые, пересекающие данную прямую и проходящую через точку вне прямой лежат в одной плоскости?

Доказать, что все прямые, пересекающие данную прямую и проходящую через точку вне прямой лежат в одной плоскости.

Видео:№147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать

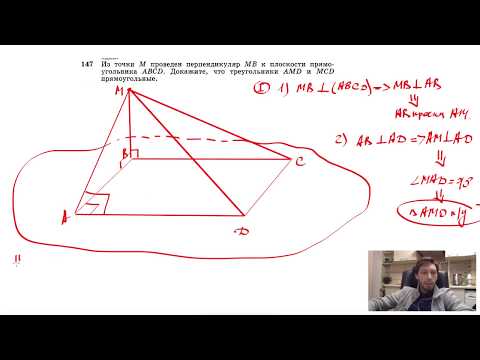
Даны пересекающиеся плоскости альфа и бета?

Даны пересекающиеся плоскости альфа и бета.

Прямая с лежит в плоскости бета и пересекает плоскость альфа в точке С.

Прямая d лежит в плоскости альфа и пересекает плоскость бета в точке D.

По какой прямой пересекаются плоскости альфа и бета?

Помогите пж — та с задачей.

На этой странице находится ответ на вопрос Точка М лежит вне плоскости четырехугольника АВСД?, из категории Геометрия, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Видео:№29. В трапеции ABCD основание ВС равно 12 см. Точка М не лежит в плоскостиСкачать

10 класс. Геометрия. Аксиомы стереометрии и их следствия.

10 класс. Геометрия. Аксиомы стереометрии и их следствия.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать

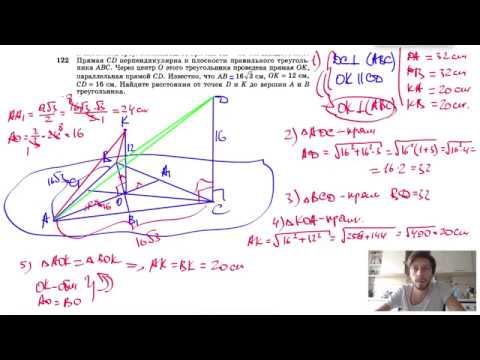
1. Напоминание аксиом стереометрии и теорем, которые следуют из них

Аксиомы стереометрии и следствия из них устанавливают взаимоотношения между основными фигурами стереометрии: точкой, прямой и плоскостью.

Точка может лежать на прямой, может не лежать на прямой.

Прямая может принадлежать плоскости, может не принадлежать плоскости.

Плоскость может проходить через прямую, не проходить через нее, содержать точку, не содержать точку.

Подобные задачи мы решали для пирамиды и для параллелепипеда. Теперь мы будем решать задачи в общем виде.

Вспомним для этого сначала аксиомы и теоремы-следствия.

Аксиома 1 (А1)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Иллюстрация аксиомы А1.

Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: (Рис. 1.). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость , и притом только одна. Плоскость можно также обозначить через три точки АВС.

Аксиома 2 (А2)

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Иллюстрация аксиомы А2. (Рис. 2.)

Аксиома 3 (А3).

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (плоскости пересекаются по прямой).

Иллюстрация аксиомы А3. (Рис. 3.)

Повторение теорем, которые следуют из аксиом стереометрии.

Теорема 1

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Иллюстрация теоремы 1. (Рис. 4.)

единственная

Теорема 2

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Иллюстрация теоремы 2. (Рис. 5.)

Видео:№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать

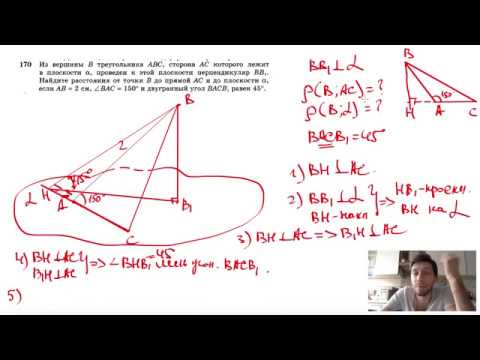
2. Решение задачи 1

Задача 1.

Даны две прямые, которые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости (Рис. 6.).

Нам даны две прямые а и b, которые пересекаются в некоторой точке М. Возьмем произвольную прямую с, которая не проходит через точку М, но пересекает исходные прямые а и b в точках А, В, соответственно.

Через две пересекающиеся прямые проходит плоскость, и притом только одна, согласно 2 теореме. Значит через пересекающиеся прямые а и b проходит единственная плоскость, обозначим ее .

Две разные точки А и В прямой с принадлежат плоскости . А из того, что две точки прямой принадлежат плоскости, вытекает, что все точки прямой принадлежат плоскости, т.е. вся прямая лежит в плоскости. Значит, прямая с принадлежит этой плоскости.

Таким образом, мы доказали, что все прямые, пересекающие А и В, но не проходящие через М, лежат в одной плоскости.

Видео:10 класс, 18 урок, Теорема о прямой, перпендикулярной к плоскостиСкачать

3. Решение задачи 2

Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.

Пусть нам даны три точки: А, В, и С. Нужно доказать, что отрезки АВ, ВС, СА лежат в одной плоскости (Рис. 7.).

Если точка С лежит на прямой АВ, то ответ очевиден. Предположим, что точка С не принадлежит прямой АВ. Тогда через три точки A, B, C, не лежащие на одной прямой, проходит плоскость, и притом только одна, в силу аксиомы 1. Обозначим эту плоскость

Прямая АВ целиком лежит в плоскости , потому что две ее точки лежат в этой плоскости. Но, значит, и отрезок АВ лежит в плоскости .

Аналогично и с другими отрезками. Прямая ВС лежит в плоскости , потому что две ее точки В и С лежат в плоскости, значит, и отрезок ВС лежит в плоскости .

И аналогично, отрезок АС лежит в плоскости . Что и требовалось доказать.

Видео:11. Прямая в пространстве и ее уравненияСкачать

4. Решение задачи 3

Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли 2 другие вершины параллелограмма в плоскости ?

Пусть дан параллелограмм АВСD. Известно: точка А, точка В, точка О – точка пересечения диагоналей, лежат в плоскости . Нужно проверить, лежат ли вершины С и D лежат также в этой плоскости.

Через три точки А, В и О проходит плоскость, и притом только одна. Это плоскость . Прямая АО целиком лежит в этой плоскости, потому что две ее точки лежат в плоскости. Значит, точка С, точка прямой АО, лежит в плоскости .

Аналогично, прямая ВО целиком лежит в плоскости , значит, точка D этой прямой тоже лежит в плоскости .

Ответ: Да, вершины С и D лежат в плоскости .

Видео:Лекция 2. Плоскость. Точка и прямая в плоскости.Скачать

5. Решение задачи 4

Дана прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.

Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам нужно доказать, что все прямые, которые проходят через точку М и пересекают прямую а лежат в некоторой единственной плоскости.

Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит единственная плоскость, обозначим через . Теперь возьмем произвольную прямую, которая проходит через точку М и пересекает прямую а, например, в точке А. Прямая МА лежит в плоскости , потому что две ее точки М и А, лежат в этой плоскости. Значит, и вся прямая лежит в плоскости , в силу 2 аксиомы.

Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи, и доказали, что она лежит в плоскости . Значит, все прямые, проходящие через точку М и пересекающие прямую а лежат в плоскости , что и требовалось доказать.

Видео:№365. Вне плоскости параллелограмма ABCD взята точка О. Точка M — середина АВ, а точка КСкачать

6. Решение задачи 5

Верно ли утверждение:

а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости;

б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?

а) Пусть дана окружность и точки А, В, С. В случае если только две точки В и С принадлежат некоторой плоскости, то совсем необязательно, что и любая другая точка окружности лежит в этой плоскости. Поэтому, данное утверждение неверно.

б) Даны три точки окружности А, В, и С. В силу аксиомы 1, через эти три различные точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Назовем эту плоскость .

Теперь докажем, что любая точка М окружности лежит в плоскости . Соединим М с А, получим точку D. Вся прямая АD лежит в плоскости , потому что две ее точки А и D лежат в плоскости . Значит, и точка Мокружности лежит в плоскости . Значит, данное утверждение верно.

Видео:🔴 В параллелограмме ABCD отмечена точка M ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

7. Решение задачи 6

Точки А, В, С и D не лежат в одной плоскости (Рис. 11.).

а) Могут ли какие-то три из них лежать на одной прямой?

б) Могут ли прямые АВ и СD пересекаться?

а) Предположим, что любые три точки, например, А, В, С лежат на одной прямой. Тогда через эту прямую и точку Dпроходит плоскость, и все 4 точки лежат в этой плоскости, что противоречит условию;

б) Нет, так как через пересекающиеся прямые можно провести плоскость, а тогда, в этой плоскости содержатся все 4 точки, что противоречит условию.

8. Решение задачи 7

а) Верно ли, что любые 3 точки лежат в одной плоскости?

Через 3 точки, если они не лежат на одной прямой, можно провести плоскость, и притом только одну, в силу аксиомы А1.

б) Верно ли, что любые 4 точки лежат в одной плоскости?

Через 3 точки можно провести плоскость, а 4 точку можно взять и в этой плоскости, и вне нее. Значит, ответ отрицательный.

в) Верно ли, что любые 4 точки не лежат в одной плоскости?

Приведем конкретный пример. Рассмотрим плоский четырехугольник, в плоскости этого четырехугольника лежат 4 точки. Итак, ответ на этот вопрос отрицательный, нет.

г) Верно ли, что через любые 3 точки проходит плоскость, и притом только одна?

Приведем пример. Возьмем 3 точки А, В, С, лежащие на одной прямой. Через них можно провести плоскость , плоскость . Через 3 точки, лежащие на одной прямой, можно провести бесконечное количество плоскостей.

9. Итоги урока

Итак, мы еще раз подытожили наши знания о стереометрии, а именно: прокомментировали три аксиомы, и два следствия из нее. И, кроме того, решили самые разнообразные задачи с использованием этих знаний.

Далее и аксиомы, и следствия будут использованы на следующих уроках при решении вопросов параллельности прямых и плоскостей.