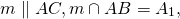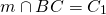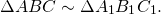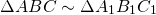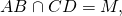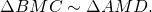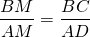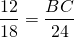Признака подобия треугольников
Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F
F’`. Напомним, что запись подобия треугольников `Delta ABC
Delta A_1 B_1 C_1` означает, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. `A` переходит в `A_1`, `B` — в `B_1`, `C` — в `C_1`.
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC
Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,
`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.
Два треугольника подобны, если:
1. два угла одного соответственно равны двум углам другого;
2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
3. три стороны одного треугольника пропорциональны трём сторонам другого.
В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.
Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.
Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.
И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.
1. Пусть `O` — точка пересечения диагоналей, `AD = a`, `BC = b`. Прямая `MN` параллельна основанию `AD` (рис. 10а), следовательно, $$ MOparallel AD$$, треугольники `BMO` и `BAD` подобны, поэтому
2. $$ ADparallel BC$$, `Delta AOD
Delta COB` по двум углам (рис. 10б):
`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.
3. Учитывая, что `BD = BO + OD` находим отношение
`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.
Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.
Точки `M` и `N` лежат на боковых сторонах `AB` и `CD` трапеции `ABCD` и $$ MNparallel AD$$ (рис. 11а). Найти длину `MN`, если `BC = a`, `AD = 5a`, `AM : MB = 1:3`.
1. Пусть $$ BFVert CD$$ и $$ MEVert CD$$ (рис. 11б), тогда `/_ 1 = /_ 2`, `/_ 3 = /_ 4` (как соответствующие углы при пересечении двух параллельных прямых третьей) и `Delta AME
Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.
2. Обозначим `MN = x`. По построению `BCNF` и `MNDE` — параллелограммы, `FN = a`, `ED = x` и, значит, `MF = x — a`; `AE = 5a — x`. Итак, имеем `(5a — x)/(x — a) = 1/3`, откуда находим `x = 4a`.
Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.
Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.
Попытайтесь доказать это самостоятельно.
Прямоугольные треугольники подобны, если:
1. они имеют по равному острому углу;
2. катеты одного треугольника пропорциональны катетам другого;
3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.
Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.
Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.
СВОЙСТВА ВЫСОТ И БИССЕКТРИС
Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C
Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).
Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).
В треугольнике `A A_1C` угол `A_1` — прямой, `A_1C = AC cos C = ul (b cos C)`.
В треугольнике `B B_1C` угол `B_1` — прямой, `B_1C = BC cos C = ul (a cos C)`.
В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.
Таким образом, `Delta A_1 B_1 C
Delta ABC` с коэффициентом подобия `ul (cos C)`. (Заметим, что `/_ A_1 B_1 C = /_B`).
б) Треугольник `ABC` — тупоугольный (рис. 12б), угол `C` — острый, высота `A A_1` проведена из вершины тупого угла.
$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cos C =b cos C;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cos C =a cos C,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC,$$
коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.
Случай, когда угол `B` тупой, рассматривается аналогично.
в) Треугольник `ABC` — тупоугольный (рис. 12в), угол `C` — тупой, высоты `A A_1` и `B B_1` проведены из вершин острых углов.
`varphi = /_ BCB_1 = /_ ACA_1 = 180^@ — /_ C`, `cos varphi = — cos C = |cos C|`.
$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cosvarphi =b |cos C|;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cosvarphi =b |cos C|,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC$$
с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.
В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).
Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).
Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).
По первой лемме о высотах `Delta A_1 B_1 C
Delta ABC`, `/_ A_1 B_1 C = /_ B`.
Аналогично `Delta AB_1C_1
Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.
Так как `BB_1` — высота, то `/_AB_1B = /_CB_1B = 90^@`.
Поэтому `/_C_1B_1B = /_A_1B_1B = 90^@ — /_B`, т. е. луч `B_1B` — биссектриса угла `A_1B_1C_1`.
Аналогично доказывается, что `A A_1` — биссектриса угла `B_1 A_1 C_1` и `C_1C` — биссектриса угла `B_1 C_1 A_1`.
Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.
Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.
Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.
1. По условию пересекаются высоты, поэтому треугольник остроугольный. Положим `BH = HB_1 = x` и `HA_1 = y`, тогда `AH = 2y`. По второй лемме о высотах `AH * HA_1 = BH * HB_1`, т. е. `x^2 = 2y^2`, `x = y sqrt 2`.
2. В треугольнике `AHB_1` угол `AHB_1` равен углу `C` (т. к. угол `A_1 AC` равен `90^@ — C`), поэтому `cos C = cos (/_ AHB_1) = x/(2y) = sqrt 2/ 2`. Угол `C` — острый, `/_ C = 45^@`.
Установим ещё одно свойство биссектрисы угла треугольника.
Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если `AD` — биссектриса треугольника `ABC`, то `(BD)/(DC) = (AB)/(AC)`.
Проведём через точку `B` прямую параллельно биссектрисе `DA`, пусть `K` — её точка пересечения с прямой `AC` (рис. 16).
Параллельные прямые `AD` и `KB` пересечены прямой `KC`, образуются равные углы `1` и `3`. Те же прямые пересечены и прямой `AB`, здесь равные накрест лежащие углы `2` и `4`. Но `AD` — биссектриса, `/_1 = /_2`, следовательно `/_3 = /_4`. Отсюда следует, что треугольник `KAB` равнобедренный, `KA = AB`.
По теореме о пересечении сторон угла параллельными прямыми из $$ ADVert KB$$ следует `(BD)/(DC) = (KA)/(AC)`. Подставляя сюда вместо `KA` равный ему отрезок `AB`, получим `(BD)/(DC) = (AB)/(AC)`. Теорема доказана.
Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.
Пусть `AD` — биссектриса и `BD = 3`, `DC = 5` (рис. 17).
По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.
Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16
Видео:Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать
Прямая, параллельная стороне треугольника
Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него треугольник, подобный данному.
Дано : ∆ ABC,
В треугольниках ABC и A1BC1
1) ∠BAC=∠BA1C1 (как соответственные при AC ∥ A1C1 и секущей AB)
Следовательно, треугольники подобны:
Что и требовалось доказать .
Продолжения боковых сторон AB и CD трапеции пересекаются в точке M. Большее основание трапеции AD равно 24 см, МС=5 см, CD=7см. Найдите меньшее основание трапеции.
Дано : ABCD — трапеция, AD ∥ BC,
AD=24 см, BM=12 см, AB=6 см
В треугольнике AMD BC — прямая, параллельная стороне AD и пересекающая две другие его стороны AM и DM. Следовательно, она отсекает от него подобный треугольник:
Из подобия треугольников следует пропорциональность их соответствующих сторон:
Если бы в задаче вместо AD и BC была задействована зависимость между MC и MD, достаточно было бы применить обобщенную теорему Фалеса для угла AMD:
Видео:Геометрия Прямая, параллельная основанию треугольника, делит его на части, площади которых относятсяСкачать
«Если через точку, взятую на боковой стороне треугольника провести прямую, параллельную основанию этого треугольника то она отсечет треугольник подобный данному» (признак подобия треугольников)
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
1. Некоторые базовые теоремы геометрии.
Базовая теорема 1
«Если через точку , взятую на боковой стороне треугольника провести прямую , параллельную основанию этого треугольника то она отсечет треугольник подобный данному» (признак подобия треугольников).
В треугольнике 
( 
— основание треугольника) через точку 
на стороне 
проведен отрезок 
, пересекающий сторону 
в точке 
.
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующее обозначение:
— отрезок проведенный через точку и пересекающий основание в точке 
.
2. С помощью теоремы
«Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов »
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) установить отношение между углами 
при условии что 
.
3.Установить отношение между углами 
при условии что 
.
4.С помощью теоремы
«Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
5.С помощью теоремы
«Если треугольники подобны то стороны лежащие против равных углов пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
6.С помощью теоремы
«Если четырехугольник является параллелограммом то противоположные стороны в нем равны»
(выражающей свойство сторон в параллелограмме) установить отношение между отрезками 
при условии что .
7.Перейти от пропорции 
к пропорции 
7. С помощью теоремы
«Если угол одного треугольника равен соответствующему углу другого треугольника , а стороны этого угла в первом треугольнике соответственно пропорциональны сторонам угла во втором треугольнике то такие треугольники будут подобны»
(выражающей признак подобия двух треугольников по двум сторонам и углу между ними) установить отношение между треугольниками 
при условии что 
.
Базовая теорема 2
«Если на сторонах угла отложить пропорциональные отрезки и через концы этих отрезков провести параллельные прямые то на второй стороне угла образуются пропорциональные отрезки с тем же коэффициентом пропорции» (теорема Фалеса)
На стороне угла 
от вершины 
отложены отрезки 
так что 
.Через точки 
проведены параллельные между собой прямые 
пересекающие вторую сторону угла соответственно в точках 
.
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующее обозначение:
— отрезок проведенный через точку 
параллельно стороне и пересекающий сторону 
в точке .
2. С помощью теоремы
«Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов »
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) установить отношение между углами 
при условии что 
.
3.С помощью теоремы
«Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
5.С помощью теоремы
«Если треугольники подобны то стороны лежащие против равных углов пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
6.С помощью теоремы
«Если четырехугольник является параллелограммом то противоположные стороны в нем равны»
(выражающей свойство сторон в параллелограмме) установить отношение между отрезками 
при условии что 
.
7.Перейти от пропорции 
к пропорции 
.
Базовая теорема 3
«Если на каждой из боковых сторон треугольника взято по одной точке так что отрезки на одной стороне пропорциональны отрезкам на другой стороне с тем же коэффициентом пропорции то отрезок , соединяющий эти точки будет параллелен третьей стороне» (теорема обратная теореме Фалеса).
В треугольнике точки взяты соответственно на сторонах 
так что 
.
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующие обозначения:
.
2.С помощью теоремы
«Если две параллельные прямые пересекаются третьей прямой то образуются пары равных углов»
(выражающей свойство углов , образованных параллельными прямыми) определить отношение между парами углов 
при условии что .
3.С помощью теоремы
«Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам) определить отношение между треугольниками 
при условии что 
.
4.С помощью теоремы
«Если два треугольника подобны то стороны лежащие в треугольниках против равных углов будут пропорциональны»
(выражающей отношение между сторонами в подобных треугольниках) определить отношение между сторонами 
при условии что 
.
5.Сравнить между собой пропорции 
.
6.С помощью теоремы
«Если в четырехугольнике две противоположные стороны равны и параллельны то он являеься параллелограммом»
(выражающей признак того что четырехугольник является параллелограммом) определить отношение между 
при условии что 
.
Базовая теорема 4
«Если в треугольнике через середину боковой стороны провести прямую , параллельную основанию треугольника то она разделит пополам смежную сторону» (частный случай теоремы Фалеса).
В треугольнике через точку , лежащей на середине стороны проведен отрезок 
.
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующее обозначение:
— дополнительное построение.
2.С помощью теоремы
«Если четырехугольник является параллелограммом то его противоположные стороны равны между собой»
(выражающей свойство сторон в параллелограмме) определить отношение между сторонами 
при условии что 
.
3.Определить отношение между отрезками 
при условии что 
.
4.С помощью теоремы
«Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что
5.С помощью теоремы
«Если в двух треугольниках две стороны и угол в одном треугольнике соответственно равны двум сторонам и углу в другом треугольнике то такие треугольники будут конгруэнтны»
(выражающей признак конгруэнтности двух треугольников по стороне и двум углам прилежащим к этой стороне) определить отношение между треугольниками 
при условии что 
.
6.С помощью теоремы
«Если два треугольника конгруэнтны то в этих треугольниках против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных треугольниках) определить отношение между сторонами 
при условии что 
.
Базовая теорема 5
«Если два треугольника подобны то отношение величин площадей этих треугольников равно квадрату отношение величин пропорциональных сторонв этих треугольниках» (свойство площадей в подобных треугольниках).
В треугольнике ( — основание треугольника) через точку на стороне проведен отрезок 
, отсекающий треугольник 
.
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующие обозначения:
— коэффициент пропорциональности сторон в подобных треугольниках;
— высота в треугольнике 
;
— высота в треугольнике
2.С помощью теоремы
«Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что
3.С помощью теоремы
«Если два прямоугольных треугольника имеют равный острый угол то они подобны»
(выражающей признак подобия прямоугольных треугольников) определить в отношение между треугольниками 
при условии что 
.
4.С помощью теоремы
«Если треугольники подобны то строны лежащие против равных углов пропорциональны»
(выражающей свойство сторон в подобных треугольниках) определить отношение между сторонами 
при условии что 
.
5.С помощью формулы 
(выражающей площадь треугольника с помощью основания и высоты) найти 
при условии что 
.
Базовая теорема 6
«Если отрезок соединяет середины двух смежных сторон треугольника то он параллелен третьей стороне и его длина равна половине длины третьей стороны» (свойство средней линии треугольника).
В треугольнике ( — основание треугольника) на сторонах 
выбраны соответственно точки так что 
.
1.Доказать что .
2.Доказать что 
.
Алгоритм управления решением:
1.Ввести следующие обозначения:
— отрезок проведенный через точку 
параллельно стороне и пересекающий продолжение 
в точке .
1. С помощью теоремы
«Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов »
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) установить отношение между углами 
при условии что 
.
2.С помощью теоремы
«Если стороны одного угла являются продолжениями сторон другого угла то такие углы равны»
(выражающей признак равенства углов с общей вершиной) установить отношение между углами 
.
3.С помощью теоремы
«Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника то такие треугольники конгруэнтны»
(выражающей признак конгруэнтности треугольников по стороне и двум углам) установить отношение между треугольниками 
при условии что 
.
4.С помощью теоремы
«Если два треугольника конгруэнтны то в них против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных треугольниках) установить отношение между сторонами 
при условии что 
5.Установить отношение между отрезками 
при условии что 
6.С помощью теоремы
«Если в четырехугольнике две противоположные стороны равны и параллельны то он является параллелограммом»
(выражающей признак параллелограма) установить отношение между сторонами 
при условии что 
1.Установить отношение между отрезкам 
при условии что 
.
Базовая теорема 7
«Если отрезок соединяет середины боковых сторон трапеции то он параллелен основаниям и его длина равна полусумме длин оснований» (свойство средней линии трапеции).
В трапеции 
( 
— соответственно нижнее и верхнее основание) проведена средняя линия (
) ,
1.Доказать что 
.
2.Доказать что 
.
Алгоритм управления решением:
1.Ввести следующее обозначение:
— отрезок, проходящий через точку 
, который пересекает продолжение основания 
(в сторону вершины ) в точке .
1.С помощью теоремы
«Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов »
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) установить отношение между углами 
при условии что 
.
2.С помощью теоремы
«Если стороны одного угла являются продолжениями сторон другого угла то такие углы равны»
(выражающей признак равенства углов с общей вершиной) установить отношение между углами 
.
3.С помощью теоремы
«Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника то такие треугольники конгруэнтны»
(выражающей признак конгруэнтности треугольников по стороне и двум углам) установить отношение между треугольниками 
при условии что 
.
4.С помощью теоремы
«Если два треугольника конгруэнтны то в них против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных треугольниках) установить отношение между сторонами 
при условии что 
5.С помощью теоремы
«Если в треугольнике проведена средняя линия то она параллельна основанию»
(выражающей свойство средней линии треугольника) установить отношение между отрезками 
при условии что 
.
1.С помощью теоремы
«Если в треугольнике провести среднюю линию то ее длина будет равна половине длины основания»
(выражающей свойство средней линии треугольника) найти при условии что 
. 
Базовая теорема 8
«Если в треугольнике из вершины угла проведена биссектриса то он делит сторону противоположную вершине на части пропорциональные сторонам угла» (свойство биссектрисы угла в треугольнике).
В треугольнике проведена виссектриса 
угла 
.
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующие обозначения:
— соответственно перпендикуляры опущенные из точки на стороны ;
— высота опущенная из вершины 
на основание .
2.С помощью теоремы
«Если точка находится на биссектрисе угла то она равноудалена от сторон этого угла»
(выражающей свойство точек , находящихся на биссектрисе) установить отношение между отрезками 
при условии что 
.
3.С помощью формулы
(выражающей площадь треугольника с помощью основания и высоты) найти площади треугольников 
.
4.Перейти от систем уравнений 
к пропорции при условии что 
.
Базовая теорема 9
«Если в окружности проведены две пересекающиеся хорды то произведение длин частей одной хорды равно произведению длин частей другой хорды» (пропорциональные отрезки в круге).
В окружности с центром 
даны две хорды 
, пересекающиеся в точке .
Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы
«Если вписанные углы опираются на одну дугу то они равны между собой»
(выражающей свойство вписанных углом) установить отношение между углами 
.
2.С помощью теоремы
«Если два угла одного треугольника соответственно равны двум углам другого треугольника то треугольники подобны»
(выражающей признак подобия треугольнико по двум углам) установит отношение между треугольниками 
при условии что 
.
3.С помощью теоремы
«Если два треугольника подобны то стороны лежащие против равных углов пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
4.Перейти от пропорции 
к произведению 
.
Базовая теорема 10
«Если из точки, лежащей вне окружности, проведены к окружности две касательные то длины отрезков этих касательных от данной точки до точек касания равны» (свойство касательных, проведенных к окружности).
Из точки , находящейся вне окружности проведены к окружности две касательные ( 
— точки касания).
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующие обозначения:
— центр окружности;
— радиусы окружности;
— отрезок , соединяющий центр окружности с данной точкой;
2.С помощью теоремы
«Если вершина угла находится на окружности , а сторонами угла являются радиус и касательная к окружности то угол равен 
»
(выражающей свойство угла, связанного с окружностью) установить величины углов 
.
3.С помощью теоремы
«Если катет и гипотенуза одного прямоугольного треугольника равны соответствующим катету и гипотенузе другого прямоугольного треугольника то такие треугольники конгруэнтны»
(выражающей признак конгруэнтности прямоугольных треугольников по катету и гипотенузе) установить отношение между треугольниками 
при условии что .
4.С помощью теоремы
«Если два треугольника конгруэнтны то в них против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных прямоугольных треугольникфх) установить отношение между сторонами при условии что 
.
Базовая теорема 11
«Если из точки, лежащей вне окружности, к окружности проведены касательная и секущая то произведение длины секущей на часть ее длины, не содержащейся в круге. равно квадрату длины касательной» (свойство касательной и секущей, проведенных из одной точки к окружности).
Из точки , лежащей вне окружности , проведена касательная к окружности и прямая , пересекающая окружность соответственно в точках 
.
Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы
«Если угол образован двумя хордами или касательной и хордой то он измеряется половиной дуги , на которую он опирается»
(выражающей свойство углов , связанных с окружностью) установить отношение между углами 
.
2.С помощью теоремы
«Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
3.С помощью теоремы
«Если два треугольника подобны то стороны в них лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
4.Перейти от пропорции 
к равенству .
Базовая теорема 12
«Если из точки, лежащей вне окружности, проведены к окружности две секущие то произведение длин отрезков одной секущей равно произведению длин отрезков другой секущей» (свойство секущих, проведенных из одной точки к окружности).
Из точки , находящейся вне окружности к окружности проведена секушая ,пересекающая окружность в точках и секущая 
, пересекающая окружность в точках .
Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы
«Если угол образован двумя хордами то он измеряется половиной дуги , на которую он опирается»
(выражающей способ измерения вписанного угла) установить отношение между углами 
.
2.С помощью теоремы
«Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
3.С помощью теоремы
«Если два треугольника подобны то стороны в них лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
п.2 Решение некоторых задач по планиметрии.
В треугольнике 
.
1.Доказать что 
.
2.Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы
«Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов »
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) установить отношение между углами 
при условии что 
.
2.С помощью теоремы
«Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника то такие треугольники будут конгруэнтны»
(выражающе признак конгруэнтности двух треугольников по стороне и двум прилежащим к ней углам) установить отношение между треугольниками 
при условии что 
.
1.С помощью теоремы
«Если два треугольника конгруэнтны то в них против равных сторон лежат равные углы»
(выражающей отношение между углами в конгруэнтных треугольниках) установить отношение между сторонами 
.
2.С помощью определения
«Четырехугольник , противоположные стороны которого параллельны, называется параллелограммом»
(выражающего определение параллелограмма) определить вид четырехугольника 
при условии что 
.
3.С помощью теоремы
«Если четырехугольник является параллелограммом то в нем противоположные стороны равны»
(выражающей отношение между противоположными сторонами в параллелограмме) установить отношение между сторонами 
.
4.Установить отношение между сторонами 
при условии что 
В треугольнике три высоты 
пересекаются в точке 
.
1.Доказать что 
.
2.Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если треугольник прямоугольный то сумма острых углов в нем равна »
(выражающей связь между углами в прямоугольном треугольнике) установить связь между углами 
.
1.С помощью теоремы «Если острый угол одного прямоугольного треугольника соответственно равен острому углу другого прямоугольного треугольника то такие прямоугольные тругольники будут подобны» (выражающей признак подобия прямоугольных треугольников по острому углу) установить отношение между прямоугольными треугольниками 
.
2.С помощью теоремы «Если два треугольника подобны то стороны , лежащие против равных углов будут пропорциональны» (выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
.
3.Определить связь между пропорциями 
.
4.С помощью теоремы «Если угол одного треугольника равен соответствующему углу другого треугольника , а стороны угла в первом треугольнике соответственно пропорциональны сторонам угла во втором треугольнике то такие треугольники будут подобны»
(выражающей признак подобия двух треугольников по двум сторонам и углу между ними) установить отношение между треугольниками 
при условии что 
.
5.С помощью теоремы «Если два треугольника подобны то углы лежащие против пропорциональных сторон будут равны между собой»
(выражающей отношение между углами в подобных треугольниках) установить отношение между углами 
при условии что 
.
1. С помощью теоремы «Если острый угол одного прямоугольного треугольника соответственно равен острому углу другого прямоугольного треугольника то такие прямоугольные тругольники будут подобны»
(выражающей признак подобия прямоугольных треугольников по острому углу) установить отношение между прямоугольными треугольниками 
.
2.С помощью теоремы «Если два треугольника подобны то стороны , лежащие против равных углов будут пропорциональны»
(выражающей отношение между сторонами в двух подобных треугольниках) определить отношение между сторонами 
.
3.Определить связь между пропорциями 
.
4. С помощью теоремы «Если угол одного треугольника равен соответствующему углу другого треугольника , а стороны угла в первом треугольнике соответственно пропорциональны сторонам угла во втором треугольнике то такие треугольники будут подобны»
(выражающей признак подобия двух треугольников по двум сторонам и углу между ними) установить отношение между треугольниками 
при условии что 
.
5.С помощью теоремы «Если два треугольника подобны то против пропорциональных сторон лежат равные углы»
(выражающей отношение между углами в двух подобных треугольниках) установить отношение между углами 
при условии что 
6.Установить отношение между углами 
при условии что 
.
В равнобедренном треугольнике 
проведена медиана к боковому ребру .
.
1.Доказать что — равносторонний.
2.Известно что 
.Вычислить длину стороны треугольника и его площадь.
Алгоритм управления решением:
1.Ввест следующие обозначения в :
— основание треугольника; 
— по построению; 
;
1.С помощью теоремы «Если две прямые перпендикулярны к одной и той же прямой то эти прямые параллельны»
(выражающей признак параллельности прямых) установить отношение между прямыми 
.
2.С помощью теоремы «Если на одной стороне угла отложены пропорциональные отрезки и через их концы проведены параллельные прямые то на другой стороне углы отложаться отрезки с сохранением пропорциональности»
(выражающей сохранение пропорциональности отрезков) установить отношение между отрезками 
.
3.С помощью теоремы «Если отрезок соединяет середины боковых сторон треугольника то он параллелен основанию треугольника и длина его равна половине длины основания»
(выражающей свойство средней линии треугольника) установить отношение между отрезками 
.
4.С помощью теоремы «Если в прямоугольном треугольнике имеется угол в тридцать градусов то длина катета , лежащего против этого угла равна половине гипотенузы этого треугольника»
(выражающей свойство угла 
в прямоугольном треугольнике) установить тношение между отрезками 
.
5.Установить отношение между отрезками 
при условии что 
.
6.С помощью теоремы «Если в треугольнике проведены две медианы то они пересекаются в одной точки и делят друг друга на части 
, считая от вершины»
(выражающей свойство медиан треугольника) установить отношение между отрезками 
при условии что 
.
7.С помощью теоремы «Если треугольник равнобедренный то в нем равны углы при основании»
(выражающей свойства углов при основании равнобедренного треугольника) установить отношение между углами 
.
8.С помощью теоремы «Если угол является внешним к треугольнику то его величина равна сумме двух величин углов треугольника , которые не являются смежными к этому углу»
(выражающей свойство внешнего угла треугольника) установить отношение между углами 
.
9.Решить уравнение 
при условии что 
.
10.С помощью теоремы «Если в любом треугольнике сложить величины всех его углов то сумма будет равна 
»
(выражающей свойство углов в треугольнике) найти величины углов треугольника при условии что 
.
1.С помощью теоремы «Если треугольник прямоугольный то квадрат длины гипотенузы равен сумме квадратов длин катетов»
(выражающей связь гипотенузы и катетов в прямоугольном треугольнике) установить отношение между отрезками 
.
2.Решить уравнение 
при условии что 
.
3.С помощью формулы 
(выражающей площадь треугольника с помощью длины основания и высоты) вычисления площади треугольника найти площадь при условии что 
.
Ответ: 2.
.
В прямоугольном треугольнике 
через точку , лежащую на гипотенузе , проведен перпендикуляр 
, пересекающий катет в точке и продолжение катета (в сторону вершины ) в точке 
. 
.
Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если треугольник прямоугольный то в нем квадрат гипотенузы равен сумме квадратов длин его катетов»
(выражающей связь между гипотенузой и катетами в прямоугольном треугольнике) найти отношение между сторонами 
.
2.Решить уравнение 
при условии что 
.
3.С помощью теоремы «Если угол одного прямоугольного треугольника равен соответствующему углу другого прямоугольного треугольника то эти треугольники подобны»
(выражающей признак подобия прямоугольных треугольников по равному острому углу) установить отношение между треугольниками 
.
4.С помощью теоремы «Если два треугольника подобны то стороны лежащие против равных углов пропорциональны»
(выражающей отношение между сторонами в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
5.Решить уравнение 
при условии что 
.
6.С помощью теоремы «Если треугольник прямоугольный то в нем квадрат длины гипотенузы равен сумме квадратов длин его катетов»
(выражающей связь между гипотенузой и катетами в прямоугольном треугольнике) установить отношение между сторонами 
.
7.Решить уравнение 
при условии что 
.
8. С помощью теоремы «Если угол одного прямоугольного треугольника равен соответствующему углу другого прямоугольного треугольника то эти треугольники подобны»
(выражающей признак подобия прямоугольных треугольников по равному острому углу) установить отношение между треугольниками 
.
9.С помощью теоремы «Если два подобных треугольника имеют равную сторону , лежащую против равного угла то они конгруэнтны»
(выражающей связь между конгруэнтностью и подобием треугольников) установить отношение между треугольниками при условии что 
.
В треугольнике проведена медиана и биссектрисы 
соответственно углов 
.
Доказать что .
Алгоритм управления решением:
1.С помощью теоремы «Если из вершины угла треугольника проведена биссектриса к некоторой стороне то она делит эту сторону пропорционально сторонам угла»
(выражающей свойство биссектрисы угла в треугольнике) определить отношение между сторонами 
.
2.Сравнить пропорции 
при условии что 
.
3.С помощью теоремы «Если на сторонах угла отложены отрезки так что на каждой из сторон сохраняется пропорциональность отрезков и если концы отрезков соединены соответствующим образом прямыми то эти прямые параллельны»
(выражающей свойство прямых , соединяющих пропорциональные отрезки) определить отношение между 
при условии что 
.
Дан параллелограмм ( 
— верхняя и нижняя стороны соответственно). На сторонах 
построены соответственно квадраты 
соответственно.
Доказать что треугольник 
является прямоугольным равнобедренным.
Алгоритм управления решением:
1.Ввести следующее обозначение:
— продолжение стороны 
в сторону вершины
1.С помощью теоремы «Если в двух треугольниках имеются две соответственно равные стороны и углы , заключенные между этими сторонами равны то токие треугольники будут конгруэнтны»
(выражающей признак конгруэнтности треугольников по двум сторонам и углу между ними) определить отношение между треугольниками 
при условии что 
.
2.С помощью теоремы «В конгруэнтных треугольниках против равных сторон лежат равные углы , а против равных углов лежат равные стороны»
(выражающей связь между сторонами и углами в конгруэнтных треугольниках) определить отношение между сторонами 
и также между парами углов 
при условии что 
.
3.С помощью теоремы «Если в треугольнике сложить величины всех углов то сумма равна »
(выражающей свойство углов в треугольнике) найти сумму величин 
.
4.Найти сумму величин углов 
при условии что 
.
5.Решить уравнение 
при условии что 
.
В треугольнике проведена медиана к стороне так что 
Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если треугольник равнобедренный то в нем углы при основании равны по величине»
(выражающей свойство углов в равнобедренном треугольнике) определить отношение между углами 
при условии что 
.
2.С помощью теоремы «Если в треугольнике сложить величины всех углов то сумма равна »
(выражающей свойство углов в треугольнике) найти сумму величин 
.
3.Решить уравнение 
при условии что 
.
В треугольнике проведена средняя линия треугольника 
параллельная основанию треугольника и биссектриса , пересекающая среднюю линию в точке .
Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если в треугольнике проведена средняя линия то она параллельна основанию»
(выражающей свойство средней линии треугольника) определить отношение между прямыми .
2.С помощью теоремы «Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов разного вида»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что
3.Определить отношение между углами 
при условии что 
.
4.С помощью теоремы «Если в треугольнике два угла равны то этот треугольник равнобедренный»
(выражающей признак равнобедренности треугольника) определить отношение между отрезками 
при условии что 
.
5.С помощью теоремы «Если в треугольнике медиана проведенная к некоторой стороне равна половине этой стороны то медиана проведена из вершины прямого угла»
(выражающей свойство медианы в прямоугольном треугольнике) определить величину угла 
при условии что 
.
В квадрате ( — нижнее основание) диагонали 
пересекаются в точке . Биссектриса 
угла 
персекает диагональ в точке и сторону в точке .
1.Найти отношения 
.
2.Доказать что 
-равнобедренный.
3.Доказать что 
.
Алгоритм управления решением:
1.Ввести следующие обозначения:
— длина стороны квадрата;
.
1.С помощью теоремы «Если треугольник прямоугольный то квадрат длины гипотенузы равен сумме квадратов длин катетов»
(выражающей отношение между сторонами в прямоугольном треугольнике) определить отношение между сторонами 
.
2.Решить уравнение 
при условии что 
.
3.С помощью теоремы «Если в треугольнике проведена биссектриса угла , лежащего против некоторой стороны то она делит эту сторону на части пропорциональные сторонам угла»
(выражающей свойство биссктрисы угла треугольника) определить отношение между отрезками 
.
4.Найти отношения 
из пропорций 
при условии что 
.
1.С помощью теоремы «Если треугольник прямоугольный то сумма острых углов в нем равна »
(выражающей свойство углов в прямоугольном треугольнике) найти углы 
.
2.С помощью теоремы «Если стороны одного угла являются продолжениями сторон другого угла то такие углы равны»
(выражающей свойство углов , имеющих общую вершину) определить отношение между углами 
.
3.Определить отношение между углами 
при условии что 
.
4.С помощью теоремы «Если в треугольнике два угла равны между собой то этот треугольник равнобедренный»
(выражающей признак равнобедренности треугольника) определить отношение между сторонами 
при условии что 
.
1.Определить отношение между отрезками 
при условии что 
.
В прямоугольном треугольнике 
проведены отрезки 
. Известно что 
.
Найти .
Алгоритм управления решением:
1. С помощью теоремы «Если треугольник прямоугольный то квадрат длины гипотенузы равен сумме квадратов длин катетов»
(выражающей отношение между сторонами в прямоугольном треугольнике) определить отношение между сторонами .
2.Решить уравнение 
при условии что 
.
3.С помощью теоремы «Если в двух прямоугольных треугольниках имеется общий острый угол то они подобны»(выражающей признак подобия прямоугольных треугольников) определить отношение между треугольниками 
.
4.С помощью теоремы «Если два треугольника подобны то стороны лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) определить отношение между сторонами 
при условии что 
.
5.Решить уравнение 
при условии что 
.
6.С помощью теоремы «Если в треугольнике провести отрезок параллельный основанию то он отсекает треугольник подобный данному»
(выражающей признак подобия двух треугольников) определить отношение между треугольниками 
.
7. С помощью теоремы «Если два треугольника подобны то стороны лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) определить отношение между сторонами 
при условии что 
.
5.Решить уравнение 
при условии что 
Ответ: 
В трапеции ( — соответственно нижнее и верхнее основания) через точку (точка пересечения диагоналей трапеции ) проведен отрезок 
. 
.
Найти .
Алгоритм управления решением:
1.С помощью теоремы «Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов разного вида»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что
2.С помощью теоремы «Если в двух треугольниках имеются два равных общих угла то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам)
определить отношение между треугольниками 
при условии что 
.
3.С помощью теоремы «Если два треугольника подобны то стороны лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) определить отношение между сторонами 
4.Определить отношения 
исходя из пропорции 
при условии что
5.С помощью теоремы «Если в треугольнике проведен отрезок параллельный основанию то он отсекает треугольник подобный данному»
(выражающей признак подобия треугольников)
определить отношение между треугольниками 
при условии что 
.
6.С помощью теоремы «Если два треугольника подобны то стороны лежащие против равных углов пропорциональны»
(выражающей свойство сторон в подобных треугольниках) определить отношение между сторонами 
при условии что 
с 
при условии что 
Ответ: 
В прямоугольнике ( — соответственно нижняя и верхняя стороны) диагонали пересекаются в точке . Сторона продлевается в сторону вершины на отрезок 
. Известно что 
.
1.Доказать что 
.
2.Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если в прямоугольном треугольнике гипотенуза вдвое больше катета то угол лежащий против катета равен »
(выражающей связь сторон в прямоугольном треугольнике) найти величину угла 
.
2.С помощью теорем : «Если четырехугольник является прямоугольником то его диагонали равны»
(выражающей свойство диагоналей прямоугольника),
«Если четырехугольник является параллелограммом то его диагонали в точке пересечения делятся на две равные части»
(выражающей свойство диагоналей параллелограмма) определить отношение между отрезками 
при условии что является одновременно параллелограммом и прямоугольником.
3.С помощью теорем: «Если фигура является треугольником то сумма углов в ней равна »
(выражающей свойство углов в треугольнике) ,
«Если треугольник является равнобедренным то в нем равны углы при основании»
(выражающей свойство углов равнобедренного треугольника) определить величины углов треугольника 
при условии что 
.
4.Определить отношение между отрезками 
при условии что 
5.С помощью теорем: «Если фигура является треугольником то сумма углов в ней равна »
(выражающей свойство углов в треугольнике) ,
«Если треугольник является равнобедренным то в нем равны углы при основании»
(выражающей свойство углов равнобедренного треугольника) определить величину угла 
при условии что 
и также 
.
6.Определить величину угла 
при условии что 
.
1.С помощью теоремы «Если в вдух треугольниках имеется пара соответственно равных сторон и углы , заключенные между этими сторонами равны то треугольники конгруэнтны»
(выражающая признак конгруэнтности двух треугольников по двум сторогам и углу между ними) определить отношение между треугольниками 
при условии что 
.
2.С помощью теоремы «Если два треугольника конгруэнтны то в них против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных треугольниках) определить отношение между сторонами 
при условии что 
.
В трапеции ( 
— соответственно нижнее и верхнее основания причем 
) через точку проведена прямая параллельная к диагонали трапеции , которая пересекает продолжение основания (в сторону вершины ) в точке . Диагонали трапеции пересекаются в точке . Площадь треугольника 
.
Найти 
.
Алгоритм управления решением:
1.Ввести следующие обозначения:
— длина стороны меньшего основания;
— высота в треугольнике 
;
— высота в треугольнике
2.С помощью формулы
(выражающей площадь треугольника с помощью основания и высоты) найти площадь треугольника 
.
3. С помощью теоремы «Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов разного вида»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что 
2.С помощью теоремы «Если в двух треугольниках имеются два равных общих угла то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам)
определить отношение между треугольниками 
при условии что 
.
3.С помощью теоремы «Если два треугольника подобны то отношение сторон равно отношению соответствующих высот»
(выражающей свойство между сторонами и высотами в подобных треугольниках) определить отношение между отрезками 
при условии что 
4.Решить уравнение 
при условии что 
.
5.С помощью формулы 
(выражающей площадь трапеции с помощью основания и высоты) найти 
при условии что 
.
6.С помощью формулы
(выражающей площадь треугольника с помощью основания и высоты) найти площадь треугольника 
при условии 
.
7.Найти 
при условии что 
.
Ответ: 
В треугольнике проведена медиана 
на сторону . Отрезки 
пересекаются в точке .Отрезки 
параллельны между собой. Известно что 
.
1.Доказать что 
.
2.Доказать что 
.
Алгоритм управления решением:
1.Ввести следующее обозначение:
— отрезок параллельный и пересекающий 
в точке .
2.С помощью определения «Четырехугольник , у которого противоположные стороны параллельны, называется параллелограммом»
(выражающим определение параллелограмма) определить вид четырехугольника 
при условии что 
.
3.С помощью теоремы «Если четырехугольник является параллелограммом то его противоположные стороны равны»
(выражающей свойство сторон в параллелограмме) определить отношение между отрезками 
.
4.С помощью теоремы «Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов разного вида»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что 
5.Определить отношение между углами 
при условии что 
.
6.С помощью теоремы «Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов разного вида»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что 
7.С помощью теоремы «Если в двух треугольниках имеется по одной равной стороне и по двум углам, которые прилежат к этой стороне то такие треугольники будут конгруэнтны»
(выражающей признак конгруэнтности двух треугольников по стороне и двум углам) определить отношение между треугольниками 
при условии что 
8.С помощью теоремы «Если два треугольника конгруэнтны то в них против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных треугольниках) определить отношение между сторонами 
при условии что 
.
9.Определить отношение между отрезками 
при условии что 
1.С помощью теоремы «Если в треугольнике провести отрезок параллельный основанию то он отсечет треугольник подобный данному»
(выражающей способ построения треугольника
подобного данному) определить отошение между треугольниками 
при условии что 
.
2.С помощью теоремы «Если два треугольника подобны то стороны лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) определить отношение между сторонами 
при условии что 
.
3.Определить отношение 
исходя из пропорции 
при условии что .
Ответ: 2.
В параллелограмме ( — соответственно нижняя и верхняя стороны) точка наъодится на стороне так что 
. Продолжение отрезка (в сторону точки встречается с продолжением стороны (в сторону вершины ) в точке 
. Известно что 
.
1.Найти площадь треугольника 
.
2.Найти площадь треугольника 
.
Алгоритм управления решением:
1.С помощью теоремы «Если стороны одного угла являются продолжениями сторон другого угла то такие углы равны»
(выражающей свойство углов с общей вершиной) определить отношение между углами 
.
2. С помощью теоремы «Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов разного вида»
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) определить отношение между углами 
при условии что 
3.С помощью теоремы «Если в двух треугольниках имеется по два соответственно равных угла то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углами) определить отношение между треугольниками 
при условии что 
.
4.С помощью теоремы «Если два треугольника подобны то отношение их площадей равно квадрату отношения их пропорциональных сторон»
(выражающей свойство площадей в подобных треугольниках) определить отношение между 
при условии что 
.
5.Решить уравнение 
при условии что 
.
1.Определить отношение между отрезками 
при условии что 
.
2.С помощью теоремы «Если в треугольнике провести отрезок параллельный основанию то он отсекает треугольник подобный данному»
(выражающей способ построения треугольник подобный данному) определить отношение между треугольниками 
при условии что 
.
3. С помощью теоремы «Если два треугольника подобны то отношение их площадей равно квадрату отношения их пропорциональных сторон»
(выражающей свойство площадей в подобных треугольниках) определить отношение между 
при условии что 
.
4.Решить уравнение 
при условии что 
.
Ответ: 
; 2.
В равнобедренном треугольнике (— основание треугольника ) проведена медиана к основанию. Точка лежит на продолжении бокового ребра (в сторону вершины ). Отрезок 
пересекает продолжение медианы в точке и через эту точку проводится отрезок 
.
1.Доказать что 
.
2.Известно что 
. Найти 
.
Алгоритм управления решением:
1.С помощью теоремы «Если в равнобедренном треугольнике проведена медианы то она является биссектрисой»
(выражающей свойство медианы в равнобедренном треугольнике) установить отношение между углами 
.
2.С помощью теоремы «Если в треугольнике проведена биссектриса к некоторой стороне то она делит эту сторону на части проплрциональные сторонам между которыми проходит»
(выражающей свойство биссектрисы в треугольнике) установить отношение между отрезками 
при условии что .
3.С помощью теоремы «Если на одной стороне угла отложить пропорциональные отрезки и через концы отрезков провести параллельные прямые то на другой стороне угла отложаться отрезки в той же пропорции»
(выражающей свойство пропорциональности отрезков) перейти от пропорции 
к пропорции
1.Решить уравнение при условии что 
.
Ответ: 2.
В треугольнике ( — основание треугольника) проведена биссектриса 
угла 
, которая пересекает сторону в точке . Через точку проведен отрезок 
, пересекающий основание в точке . Известно что 
.
Найти .
Алгоритм управления решением:
1.С помощью теоремы «Если две параллельные прямые пересечь третиьей то будут образованы пары равных углов »
(выражающей отношение между углами , образованными при пересечении двух параллельных прямых третьей) установить отношение между углами 
при условии что .
2.Установить отношение между углами 
при условии что 
.
3.С помощью теоремы «Если в треугольнике есть два равных угла то этот треугольник равнобедренный»
(выражающий признак равнобедренного треугольника) установить отношение между сторонами 
при условии что 
.
4.С помощью теоремы «Если в треугольнике провести отрезок параллельный основанию то он отсечет треугольник подобный данному»
(выражающей способ построения треугольника подобного данному) установить отношение между треугольниками 
при условии что .
5.С помощью теоремы «Если треугольники подобны то стороны лежащие против равных углов пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами при условии что 
.
6.Решить уравнение 
при условии что 
.
Ответ: 
В треугольнике ( — основание треугольника) проведены высоты 
, пересекающиеся в точке причем 
.
1.Доказать что 
.
2.Доказать что 
.
3.Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если два катета одного прямоугольного треугольника равны соответствующим двум катетам другого прямоугольного треугольника то такие треугольники конгруэнтны»
(выражающей признак конгруэнтности прямоугольных треугольников по двум катетам) установить отношение между треугольниками 
при условии что .
2.С помощью теоремы «Если два прямоугольных треугольника конгруэнтны то против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных треугольниках) установить отношение между отрезками 
при условии что 
.
1. С помощью теоремы «Если два прямоугольных треугольника конгруэнтны то против равных сторон лежат равные углы»
(выражающей свойство углов в конгруэнтных треугольниках) установить отношение между углами 
при условии что .
2.С помощью теоремы «Если стороны одного угла являются продолжением сторон другого угла то такие углы равны»
(выражающей свойство углов с общей вершиной) установить отношение между углами 
.
3.С помощью теоремы «Если сторона и два прилежащих к ней угла одного треугольника равны соответствующим стороне и двум прилежащим к ней углам другого треугольника то такие треугольники конгруэнтны»
(выражающей признак конгруэнтности двух треугольников по стороне и двум углам) установить отношение между треугольниками 
при условии что 
.
4.С помощью теоремы «Если два треугольника конгруэнтны то в них против равных углов лежат равные стороны»
(выражающей свойство сторон в конгруэнтных треугольниках) установить отношение между сторонами 
при условии что 
.
В треугольнике три высоты пересекаются в точке .
Доказать что четырехугольник 
можно вписать в окружность.
Алгоритм управления решением:
1.С помощью теоремы «Если в четырехугольнике сумма противоположных углов равна то его можно вписать в окружность»
(выражающей условие вписания в окружность четырехугольника) найти сумму углов 
при условии что 
и зная что сумма углов четырехугольника равна 
.
В окружности с центром и радиусом 
диаметр перпендикулярен хорде и пересекается с ней в точке . Известно что 
.
Найти площадь треугольника 
.
Алгоритм управления решением:
1.Решить уравнение 
при условии что 
.
2.С помощью теоремы «Если в окружности проведены две пересекающиеся хорды то произведение частей одной хорды равно произведению частей другой хорды»
(выражающей свойство частей хорды) установить отношение между отрезками 
.
3.С помощью теоремы «Если диаметр перпендикулярен к хорде то он делит ее на две равные части»
(выражающей свойство диаметра) установить отношение между отрезками 
.
4.Решить уравнение при условии что 
.
4.С помощью формулы 
(выражающей площадь треугольника по основанию и высоте) найти при условии что 
.
Ответ: 
Четырехугольник вписан в окружность. является биссектрисой угла . Через точку проведена касательная , которая пересекает продолжения сторон (в сторону вершин 
соответственно в точках 
.
1.Доказать что 
.
2.Доказать что 
.
3.Известно что 
. Найти .
Алгоритм управления решением:
1.С помощью теоремы «Если четырехугольник можно вписать в окружность то сумма противоположных углов в нем равна »
(выражающей свойство углов вписанного в окружность четырехугольника) найти сумму 
.
2.С помощью теоремы «Если углы являются смежными то они в сумме составляют »
( выражающей свойство смежных углов) найти сумму 
.
3.Установить отношение между углами 
при условии что 
.
1.С помощью теоремы «Если угол висан в окружность или составлен касательной и хордой то он измеряется половиной дуги , на которую он опирается»
(выражающей свойство вписанного угла и угла образованного касательной и хордой) установить отношение между углами 
.
2.С помощью теоремы «Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
1.С помощью теоремы «Если дуги равны то на них опираются равные хорды»
(выражающей свойство хорд) установить отношение между отрезками 
при условии что .
2.С помощью теоремы «Если два треугольника подобны то стороны лежащие против равных углов пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между отрезками 
при условии что 
.
3.Решить уравнение 
при условии что 
.
Ответ: 
Окружность с центром касается некоторой прямой в точке . Через центр окружности проходит диаметр . Через концы диаметра проведены касательные соответственно 
, пересекающие вышеуказанную прямую соответственно в точках 
.
1.Доказать что 
.
2.Доказать что 
.
3.Известно что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если проведена касательная к окружности то она составляет угол с радиусом этой окружности в точке касания»
(выража.щей свойство касательной к окружности) установить величины углов 
.
2.С помощью теоремы «Если из точки вне окружности провести две касательные к окружности то отрезки касательных от указанной точки до точек касания будут равны»
(выражающей свойство касательных к окружности) установить отношение между отрезками 
.
3.С помощью теоремы «Если точка равноудалена от сторон угла то она находится на биссектрисе этого угла»
(выражающей свойство биссектрисы угла) установить отношение между углами 
.
4.Найти сумму величин углов 
при условии что 
1.С помощью теоремы «Если треугольник прямоугольный то сумма острых углов в нем равна »
(выражающей свойство острых углов в прямоугольном треугольнике) найти углы 
.
2.С помощью теоремы «Если острый угол в одном прямоугольном треугольнике равен соответствующему острому углу в другом прямоугольном треугольнике то такие треуголшьники подобны»
(выражающей признак подобия прямоугольных треугольников) установить отношение между треугольниками 
при условии что 
.
1.С помощью теоремы «Если треугольники подобны то стороны, лежащие в них против равных углов, пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
2.Решить уравнение 
при условии что 
.
Ответ: 3.
Из точки , лежащей вне окружности проведена секущая 
, пересекающая окружность в точках 
(причем точка находится вне окружности) и касательная .Проводят хорду 
и через точку проводят прямую параллельную этой хорде , которая не пересекает окружность , но пересекает продолжение касательной касательной в точке 
.
1.Доказать что 
.
2.Доказать что четырехугольник 
можно вписать в окружность.
Алгоритм управления решением:
1.С помощью теоремы «Если угол образован двумя хордами или касательной и секущей то он измеряется половиной дуги на которую он опирается»
(выражающей способ измерения углов , связанных с окружностью) установить отношение между углами 
.
1.С помощью теоремы «Если углы являются смежными то сумма их величин равна »
(выражающей свойство смежных углов) найти сумму величин углов 
.
2.С помощью теоремы «Если две параллельные прямые пересечь третьей прямой то образуются пары равных углов»
(выражающей свойство углов, образованных параллельными прямыми) установить отношение между углами 
при условии что 
.
3.С помощью теоремы «Если сумма величин противоположных углов четырехугольника равна то этот четырехугольник можно вписать в окружность»
(выражающей признак вписания четырехугольника в окружность) найти сумму величин углов 
при условии что 
.
В равнобедренный треугольник 
( — основание треугольника) вписана окружность, касающаяся основания в точке и боковых сторон 
соответственно в точках . Известно что 
.
1.Доказать что 
.
2.Найти .
Алгоритм управления решением:
1.С помощью теоремы «Если из точки вне окружности провести к окружности две касательные то отрезки касательных от указанной точки до точек касания будут равны»
(выражающей свойство касательных к окружности) установить отношение между отрезками 
.
2.С помощью теоремы «Если треугольник равнобедренный то в нем равны углы при основании»
(выражающей свойство углов в равнобедренном треугольнике) установить отношение между углами 
.
3.С помощью теоремы «Если сложить величины углов треугольника то сумма будет равна »
(выражающей свойство величин углов треугольника) найти значение величин углов 
4.С помощью теоремы «Если при пересечении двух прямых третьей соответственные углы равны то прямые параллельны»
(выражающей признак параллельности прямых) установить отношение между отрезками 
при условии что 
.
1.Найти 
при условии что 
2.С помощью теоремы «Если в треугольнике проведена линия параллельно основанию то она отсекает от него треугольник подобный данному»
(выражающей способ построения треугольника подобного данному) установить отношение между треугольниками 
при условии что .
3.С помощью теоремы «Если два треугольника подобны то стороны лежащие в них против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
4.Решить уравнение 
при условии что 
.
Ответ: 2.
В прямоугольный треугольник 
вписана полуокружность , касающаяся катетов 
соответственно в точках 
и центр которой находится на гипотенузе 
. Известно что 
.
1.Доказать что 
.
2.Найти 
.
Алгоритм управления решением:
1.С помощью теоремы «Если угол образован радиусом окружности и касательной с вершиной в точке касания то он равен »
(выражающей признак прямого угла) установить величины углов 
.
2.С помощью теоремы «Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника то такие треугольники конгруэнтны»
(выражающей признак конгруэнтности прямоугольных треугольников) установить отношение между треугольниками 
при условии что .
3.С помощью теоремы «Если два треугольника конгруэнтны то в них против равных сторон лежат равные углы»
(выражающей свойство сторон в конгруэнтных треугольниках) установить отношение между углами 
.
1.С помощью теоремы «Если треугольник является прямоугольным то квадрат длины гипотенузы равен сумме квадратов длин катетов»
(выражающей свойство сторон в прямоугольном треугольнике) установить отношение между сторонами 
.
2.Решить уравнение 
при условии что .
3.С помощью теоремы «Если острый угол одного прямоугольного треугольника равен соответствующему острому углу другого прямоугольного треугольника то такие треугольники подобны»
(выражающей признак подобия прямоугольных треугольников по острому углу) установить отношения между треугольниками 
.
4.С помощью теоремы «Если два треугольника подобны то стороны лежащие в них против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
5.Решить уравнение 
при условии что 
.
Ответ: 2.
Треугольник 
вписан в окружность. Прямая 
касается этой окружности в точке . Через точку проведена прямая 
.
1.Доказать что 
.
2.Известно что 
.Найти 
.
Алгоритм управления решением:
1.С помощью теоремы «Если угол образован касательной и хордой или двумя хордами то он измеряется половиной дуги на которую опирается»
(выражающей способ измерения углов , связанных с окружностью) установить отношение между углами 
.
2.С помощью теоремы «Если две параллельные прямые пересекаются третьей то при этом образуются пары углов равных между собой»
(выражающей свойство углов , образованных параллельными прямыми) установить отношение между углами 
при условии что .
3.Установить отношение между углами 
при условии что 
.
4.С помощью теоремы «Если два угла одного треугольника равны соответствующим двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
1.С помощью теоремы «Если два треугольника подобны то стороны лежащие в них против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
2.Решить уравнение 
при условии что 
.
Ответ: 2.
В треугольник 
( — основание треугольника) вписана окружность , касающаяся основания в точке , а боковых сторон 
в точках соответственно. Биссектриса угла 
делит основание треугольника на части 
так что 
. Известно что 
.
Найти стороны .
Алгоритм управления решением:
1.С помощью теоремы «Если из точки вне окружности провести две касательные к окружности то длины отрезков этих касательных от указанной точки до точек касаия будут равны»
(выражающей свойство касательных проведенных к окружности) установить отношение между отрезками 
.
2.С помощью теоремы «Если в треугольнике провести биссектрису угла то она разделит сторону противоположную этому углу на части пропорциональные сторонам угла»
(выражающей свойство биссектрисы угла в треугольнике) установить отношение между отрезками 
.
3.Решить систему уравнений 
при условии что 
.
Ответ: 
Равнобедренный треугольник ( — основание треугольника) вписан в окружность. Через точку проведена касательная к окружности , которая пересекает прямую 
в точке . Известно что 
.
1.Доказать что 
.
2.Найти .
Алгоритм управления решением:
1.С помощью теоремы «Если угол образован касательной и хордой или двумя хордами то он измеряется половиной дуги на которую опирается»
(выражающей способ измерения углов , связанных с окружностью) установить отношение между углами 
.
2.С помощью теоремы «Если две параллельные прямые пересекаются третьей то при этом образуются пары углов равных между собой»
(выражающей свойство углов , образованных параллельными прямыми) установить отношение между углами 
при условии что .
3.С помощью теоремы «Если два угла одного треугольника равны соответствующим двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия двух треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
1.С помощью теоремы «Если два треугольника подобны то стороны лежащие в них против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
2.Решить уравнение 
при условии что .
Ответ: 2. 
В равнобедренную трапецию ( — соответственно нижнее и верхнее основание) вписана окружность , касающаяся оснований соответственно в точках и боковых сторон 
соответственно в точках .
1.Доказать что 
.
2.Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если провести радиус в точку касания прямой с окружностью то угол образованный радиусом с касательной равен »
(выражающая свойство угла , образованного радиусом и касательной) установить величины углов 
.
2.С помощью теоремы «Если точка равноудалена от сторон угла то она находится на биссектрисе этого угла»
(выражающей свойство точек , находящихся на биссектрисе) установить отношение между углами 
.
3.С помощью теоремы «Если при пересечении двух параллельных прямых третьей образуются углы прилежащие к третьей прямой то сумма их величин равна »
(выражающей свойство углов , образованных параллельными прямыми) найти сумму 
при условии что 
.
4.Найти величину угла 
при условии что 
.
5.С помощью теоремы «Если треугольник прямоугольный то сумма острых углов в нем равна »
(выражающей свойство острых углов в прямоугольном треугольнике) установить величины углов 
при условии что 
.
6.С помощью теоремы «Если острый угол в одном прямоугольном треугольнике равен соответствующему острому углу в другом прямоугольном треугольнике то такие треугольники подобны»
(выражающей признак подобия прямоугольных треугольников по острому углу) установить отношение между треугольниками 
при условии что 
.
7.С помощью теоремы «Если треугольники подобны то стороны в них лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между отрезками 
при условии что 
.
8.Перейти от пропорции 
к отношению 
.
1.С помощью теоремы «Если из точки вне окружности провести две касательные к окружности то длины отрезков этих касательных от указанной точки до точек касаия будут равны»
(выражающей свойство касательных проведенных к окружности) установить отношение между отрезками 
.
2.Перейти от равенства к равенству 
при условии что 
.
В трапеции ( — соответственно нижнее и верхнее основании трапеции) основание и боковая сторона являются хордами окружности в то время как боковая сторона касается этой окружности в точке .
1.Доказать что 
.
2.Известно что 
. Найти .
Алгоритм управления решением:
1.С помощью теоремы «Если угол образован двумя хордами или касательной и хордой то он измеряется половиной дуги , на которую он опирается»
(выражающей свойство углов , связанных с окружностью) установить отношение между углами 
.
2.С помощью теоремы «Если две параллельные прямые пересекаются третьей прямой то образуются пары равных между собой углов»
(выражающей свойство углов , образуемых параллельными прямыми) установить отношение между углами 
при условии что .
3.С помощью теоремы «Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
1.С помощью теоремы «Если два треугольника подобны то стороны в них лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
2.Решить уравнение 
при условии что .
Ответ: 2. 
Из точки , находящейся вне окружности проведена секущая , пересекающая окружность в точках и секущая , пересекающая окружность в точках 
. Известно что 
.
Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия треугольников по двум углам) установить отношение между треугольниками 
при условии что 
.
2.С помощью теоремы «Если в треугольнике два угла равны то этот треугольник равнобедренный»
(выражающей признак равнобедренности треугольника) установить отношение между отрезками 
при условии что 
.
3.С помощью теоремы «Если два треугольника подобны то стороны в них лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
4Перейти от пропорции 
к равенству 
при условии что 
.
— диаметр окружности с центром . Точки соединены с точкой , лежащей вне окружности , соответственно отрезками 
. Отрезок 
пересекает окружность в точке 
и через эту точку проведена касательная к окружности , перепендикулярная к отрезку и пересекающая его в точке .
1.Доказать что 
.
2.Доказать что 
.
Алгоритм управления решением:
1.С помощью теоремы «Если угол образован двумя хордами или касательной и хордой то он измеряется половиной дуги , на которую он опирается»
(выражающей свойство углов , связанных с окружностью) установить отношение между углами 
.
2.С помощью теоремы «Если угол одного прямоугольного треугольника соответственно равен углу другого прямоугольного треугольника то такие треугольники подобны»
(выражающей признак подобия прямоугольных треугольников по острому углу) установить отношение между треугольниками 
при условии что 
.
3.С помощью теоремы «Если два треугольника подобны то стороны в них лежащие против равных углов будут пропорциональны»
(выражающей свойство сторон в подобных треугольниках) установить отношение между сторонами 
при условии что 
.
4.Перейти от пропорции 
к равенству 
.
1.С помощью теоремы «Если стороны одного угла соответственно перпендикулярны сторонам другого угла то такие углы равны»
(выражающей свойство углов с соответственно перпендикулярными сторонами) установить отношение между углами 
при условии что 
.
2.Установить отношение между углами 
при условии что 
.
3.С помощью теоремы «Если в треугольнике равны два угла то этот треугольник равнобедренный»
(выражающей признак равнобедренности треугольника) установить отношение между сторонами 
при условии что 
.
4.С помощью теоремы «Если треугольник равнобедренный то высота в нем является медианой»
(выражающей свойство высоты в равнобедренном треугольнике) установить отношение между отрезками 
при условии что 
.
Треугольник 
( — основание треугольника) вписан в окружность. Биссектриса угла пересекает основание в точке и окружность в точке . Точка делит основание на части 
. Из точки на основание опущен перпендикуляр .
Доказать что 
Алгоритм управления решением:
1.С помощью теоремы «Если в треугольнике проведена биссектриса угла то она делит сторону противоположную углу на части пропорциональные сторонам угла»
(выражающей свойство биссектрисы угла) установить отношение между отрезками при условии что .
2.Установить отношение 
при условии что 
.
3.С помощью теоремы «Если угол вписан в треугольник то он измеряется половиной дуги на которую он опирается»
(выражающей способ измерения вписанного угла) установить отношения между дугами 
при условии что 
.
4.С помощью теоремы «Если дуги окружности равны то равны и хорды опирающиеся на эти дуги»
(выражающей свойство хорд в окружности) установить отношение между отрезками 
при условии что 
.
5.С помощью теоремы «Если в равнобедренном треугольнике проведена высота то она является медианой»
(выражающей свойство высоты в равнобедренном треугольнике) установить отношение между отрезками 
при условии что 
.
6.Найти при условии что 
.
Две окружности касаются друг друга внешним образом в точке .Через эту точку проведена прямая , пересекающая одну из окружностей в точках 
и другую окружность в точках 
. Другая прямая , проведенная через эту же точку , пересекает одну окружность в точках 
и другую окружность в точках 
.
Доказать что 
.
Алгоритм управления решением:
1.Ввести следующее обозначение:
— общая касательная к двум окружностям;
2.С помощью теоремы «Если угол образован касательной и хордой или двумя хордами то он измеряется половиной дуги , на которую он опирается»
(выражающей способ измерения углов , связанных с окружностью) установить отношения между углами 
.
3.С помощью теоремы «Если стороны одного угла являются продолжением сторон другого угла то такие углы равны»
(выражающей свойство углов с общей вершиной) установить отношение между углами 
.
4.Установить отношение между углами 
при условии что 
и также при условии что 
.
5.С помощью теоремы «Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие треугольники подобны»
(выражающей признак подобия треугольников по двум углам) установить отношение между треугольниками 
при условии что 
. .
🔥 Видео
№241. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВСкачать
Геометрия Длина основания треугольника равна 36 см. Прямая, параллельная основанию, делит площадьСкачать
Задание 3 ЕГЭ по математике. Урок 41Скачать
Средняя линия. Теорема о средней линии треугольникаСкачать
Параллельные прямые | Математика | TutorOnlineСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать
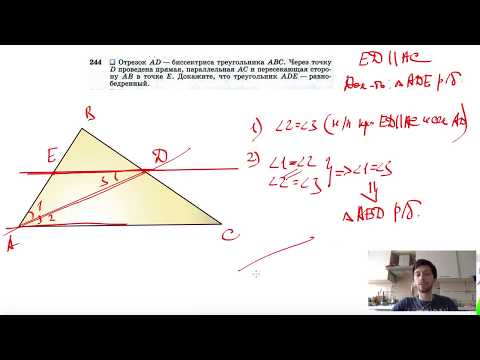
№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать
Основная теорема о пропорциональностиСкачать
Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать
Средняя линия треугольника и трапеции. 8 класс.Скачать
Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать
🔺📏 Теорема Вариньона: Новая глава геометрии! 🔺📏Скачать
Теорема о средней линии треугольникаСкачать
8 класс, 25 урок, Средняя линия треугольникаСкачать
ЗАДАНИЕ 1|ЕГЭ ПРОФИЛЬ| Площадь треугольника ABC равна 52, DE-средняя линия, параллельная стороне AB.Скачать
Параллельность прямых. 10 класс.Скачать
№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать
