Все о BIM, CAD, ERP
- Как создать дугу заданной длины
- Аниматик по длинне дуги в автокаде.
- 7 комментариев
- Сегмент круга
- Формулы вычисления параметров сегмента
- Как построить окружность по хордам
- Сегмент круга
- Формулы вычисления параметров сегмента
- Построение дуги окружности по хорде и вписанному углу
- Построение дуги окружности по хорде и вписанному углу
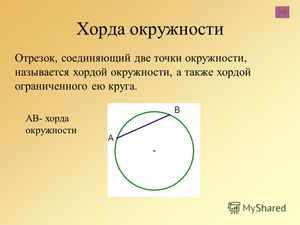
- Что такое хорда окружности в геометрии, её определение и свойства
- Как построить геометрическую хорду
- Свойства
- Взаимосвязь с радиусом и диаметром
- Хорда и радиус
- Отношения со вписанными углами
- Взаимодействия с дугой
- 📸 Видео
Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Как создать дугу заданной длины

Самый очевидный выход — вычислить необходимые параметры дуги с помощью простых математических действий из раздела аналитической геометрии. По радиусу и необходимой длине вычислить угол сектора, и уже с его мощью создать дугу требуемой длинны. Но согласитесь — это довольно запарно.
Впрочем есть и другой вариант:
- Нарисовать дугу требуемого радиуса.
- Затем изменить её с помощью инструмента Увеличить (lengthen).
С его помощью вы можете изменить полную длину объекта — любого объекта, в том числе и дуги. Выберите опцию ВСЕГО и введите требуемое значение:
Команда: _lengthen
Выберите объект для измерения или [ДЕльта/проЦент/Всего/ДИнамика] :
Текущая длина: 736.3428, внутренний угол: 151
Выберите объект для измерения или [ДЕльта/проЦент/Всего/ДИнамика] : В
Укажите общую длину или [Угол] : 500
Теперь можно посмотреть в свойства и убедиться, что длинна дуги равна требуемому значению:
Видео:Длина дуги окружности. 9 класс.Скачать

Аниматик по длинне дуги в автокаде.
Однако, лично я не сталкивался в своей практике с необходимостью в подобных построениях. Кто-нибудь знает зачем это вообще может пригодится?
Видео:Длина окружности. Математика 6 класс.Скачать

7 комментариев
Да. Нужно было начертить развертку части усеченного конуса для раскладки на плазме.
Надо было прокатать на вальцах деталь определённого радиуса имея определённую длину развёртки. Пригодилоссь, спасибо!
Видео:Окружнось, дуга, длина дуги, центральный угол.Скачать

Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Видео:Радиус и диаметрСкачать

Как построить окружность по хордам
Видео:ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Построение дуги окружности по хорде и вписанному углу

Видео:Параметризация длины дуги окружностиСкачать

Построение дуги окружности по хорде и вписанному углу
Композиция дуги и вписанный угол окружности вдоль хорды. Из геометрии известно, что вписанный угол — это угол, под которым вершина расположена на окружности, а стороны-это струны.
- Вписанный угол измеряется в половине дуги, на которой он расположен. Поэтому./,ABC =(рисунок 139) измеряется-АЦП, А. / АЦП 2 Измерение-Азбука. Сумма 2 углов/ ABC + ADC = L.
Поскольку угол EDC добавляется к l / AOSU, он становится / EDC-ty. Людмила Фирмаль
Какую бы позицию ни занимала позиция D в интервале от A до C, угол между продолжением кода AD (то есть линией DE) и кодом DC не изменяется и остается равным φ.
Угол между продолжением кода переменного тока и касательной окружности в точке С также равен углу ip. Центр окружности О находится в точке пересечения перпендикуляра к середине хорды и касательной (рис. 140).
- Из вышеизложенного, если хорды и вписанный угол указаны, чтобы найти центр окружности (см. Рисунок 140), вам нужно: V * Г.
1.Восстановите средний перпендикуляр строки.
2.Нарисуйте прямую линию, касательную к окружности, под углом φ к продолжению хорды. Людмила Фирмаль
3.Восстанавливает перпендикуляр к касательной.
Точка пересечения перпендикуляра относительно струны и касательной дает центр окружности.



















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Что такое хорда окружности в геометрии, её определение и свойства
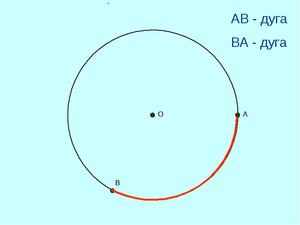
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
Видео:Длина дуги окружностиСкачать

Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Видео:+Как найти длину окружностиСкачать

Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
- Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
- Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Видео:Окружнось. Зависимость длины хорды, от длины дуги.Скачать

Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Хорда и радиус
Между этими понятиями существуют следующие связи:
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Видео:Длина дуги окружности. Практическая часть. 9 класс.Скачать
Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
📸 Видео
Как найти длину дуги окружности центрального угла. Геометрия 8-9 классСкачать

КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Нахождение длины дуги кривойСкачать







 Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой. Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.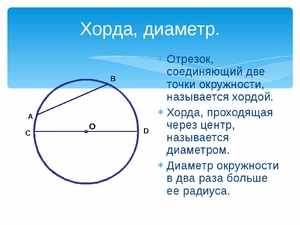 Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.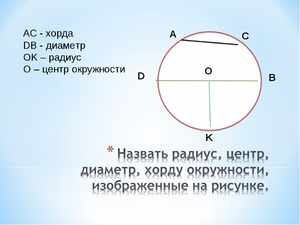 Две равные между собой хорды стягивают равные дуги.
Две равные между собой хорды стягивают равные дуги.