- Определение окружности, вписанной в треугольник
- Теорема об окружности, вписанной в треугольник
- Теорема об окружности вписанной в треугольник сколько окружностей можно
- Как написать хороший ответ?
- Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- 🎥 Видео
Видео:Теорема об окружности вписанной в треугольникСкачать

Определение окружности, вписанной в треугольник
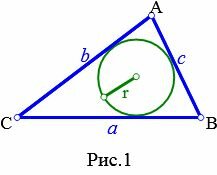
Определение 1. Окружностью, вписанной в треугольник называется окружность, которая находится внутри треугольника и касается всех его сторон (Рис.1).
 |
Можно дать и другое определение окружности, вписанной в треугольник.
Определение 2. Окружностью, вписанной в треугольник называется наибольшая окружность, которая может находится внутри треугольника.
При этом треугольник называется треугольником описанным около окружности . Центр вписанной в треугольник окружности явлется точка пересечения биссектрис треугольника. Центр окружности вписанной в треугольник называется инцентром треугольника.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Теорема об окружности, вписанной в треугольник
Теорема 1. В любой треугольник можно вписать окружность.
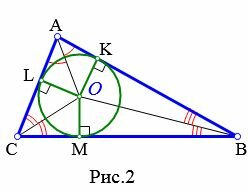 |
Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения биссектрис треугольника. Проведем из точки O перпендикуляры OK, OL и OM к сторонам AB, AC, BC, соответственно. Поскольку точка O равноудалена от сторон треугольника ABC, то OK=OL=OM. Тогда окружность с центром O и радиусом OK проходит через три точки K, L, M. Стороны AB, AC, BC треугольника ABC касаются этой окружности в точках K, L, M, поскольку они перпендикулярны к радиусам OK, OL, OM, соответственно. Следовательно, окружность с центром O и радиусом OK является вписанной в треугольник ABC.
Замечание 1. В любой треугольник можно вписать только одну окружность.
Доказательство. Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из этих окружностей равноудален от сторон треугольника и совпадает с точкой O пересечения биссектрис треугольника. Радиус этих окружностей равен расстоянию от точки O до сторон треугольника. Поэтому эти окружности совпадают.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Теорема об окружности вписанной в треугольник сколько окружностей можно
Вопрос по геометрии:
сформулируйте и докажите теорему об окружности вписанной в треугольник? сколько окружностей можно вписать в данный треугольник?
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Доказательство.
Пусть ABC данный, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Δ AEO = Δ AOD по гипотенузе и катету (EO = OD – как радиус, AO – общая). Из равенства треугольников следует, что ∠ OAD = ∠ OAE. Значит AO биссектриса угла EAD. Точно также доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.
В треугольник всегда можно вписать окружность,и при том только одну.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
 Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
🎥 Видео
Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Окружность, вписанная в треугольникСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

8 класс, 38 урок, Вписанная окружностьСкачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Радиус описанной окружностиСкачать

#233. Теоремы синусов и косинусов | Формулы радиусов окружностейСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Треугольник и окружность #shortsСкачать






























