В треугольнике abc прямая параллельная стороне ac делит сторону bc на отрезки

Решение:
Дано: треугольник АВС MN//AC (параллельно) BN = 15 см NC = 5 см АС = 15 см Найти: MN — ? Решение: MN параллельно AC ==> угол BAC = углу BMN u угол BNM = углу BCA ==> треугольник АВС подобен треугольнику MBN ==> MN/AC = BN/BC (пропорция) ВС = BN + NC = 15 + 5 = 20 см MN/15 = 15/20 = $$ frac = 11,25 $$ Ответ: MN = 11,25 см

Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

В треугольнике abc прямая параллельная стороне ac делит сторону bc на отрезки

Площадь треугольника АВС равна 12. На прямой АС взята точка D так, что точка С является серединой отрезка AD. Точка K — середина стороны AB, прямая KD пересекает сторону BC в точке L.

a) Докажите, что BL : LC = 2 : 1.

б) Найдите площадь треугольника BLK.

а) Соединим отрезками точки B и D, A и L. Рассмотрим треугольник АВD. Ясно, что L — точка пересечения медиан этого треугольника. Отсюда BL : LC = 2 : 1, что и требовалось доказать.

б) Как известно, медианы треугольника, пересекаясь в одной точке, делят его на 6 равновеликих треугольников. Учитывая то, что L — точка пересечения медиан а также получим:

Точка D делит сторону AC в отношении AD : DC = 1 : 2.

а) Докажите, что в треугольнике ABD найдётся медиана, равная одной из медиан треугольника DBC.

б) Найдите длину этой медианы в случае, если AB = 7, BC = 8, и AC = 9.

а) Обозначим середины отрезков BA, BD, BC за E, F, G соответственно. Тогда EG — средняя линия треугольника ABC, и точка F лежит на ней. Поскольку FG — средняя линия DBC, то Итак, в четырехугольнике AFGD две стороны равны и параллельны, значит, он параллелограмм и

б) По теореме косинусов в треугольнике ABC имеем откуда

По теореме косинусов в треугольнике DGC имеем откуда

Ответ:

Площадь треугольника ABC равна 10; площадь треугольника AHB, где H — точка пересечения высот, равна 8. На прямой CH взята такая точка K, что треугольник ABK — прямоугольный.

а) Докажите, что

б) Найдите площадь треугольника ABK.

а) Заметим, что поскольку тогда или как перпендикуляры к одной прямой. Значит, Обозначим основания высот треугольника ABC за Тогда точки K, B, A, A₁, B₁ лежат на окружности с диаметром AB (из-за прямых углов). заметим, что — основание перпендикуляра из K на

Перепишем требуемое утверждение:

Это верно из-за подобия треугольников AHS и CBS по двум углам: действительно,

б) Из пункта а) следует, что

Ответ:

Видео:№538. Биссектриса AD треугольника ABC делит сторону ВС на отрезки CD и BD, равные соответственноСкачать

Формирование умений учащихся и их наставников к решению и объяснению заданий ЕГЭ

Видео:Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Педагогические науки

• Баталаев Арслан Викторович , аспирант
• Калмыцкий государственный университет

• ПЛАНИМЕТРИЧЕСКИЕ ЗАДАЧИ
• ФОРМИРОВАНИЕ УМЕНИЙ
• ЕГЭ

Видео:ОГЭ Р-2 номер 16Скачать

Похожие материалы

Большинство населения воспринимают ЕГЭ как более объективную, более справедливую по сравнении с существовавшей системой вступительных экзаменов (до 2005 г). Заметим, что английские to test означают — «проверять». У нас же в обществе слово «тест» воспринимается как выбор ответа из нескольких предложенных.

В организационном плане процедура ЕГЭ была заимствована из практики большинства стран Европы.

В последнее время произошли качественные изменения в использовании и понимании обществом социально-ориентируемой математической информацией в заданиях ОГЭ, ЕГЭ. Всё большее количество людей, прямо или косвенно являются учителями и советниками учащихся, обсуждая с ними содержание заданий.

Сейчас особенно активны родители или родственники выпускников, получившие физико-математическое или техническое образование в советское время. Для того, чтобы составить очень много различных по числовым параметрам заданий, необходимо правильно и удачно выбрать линейку основных примеров. Здесь очень важна информационная база знаний о предмете. Решение любой геометрической задачи предполагает определенный теоретический баланс и вполне естественно, что чем он больше, тем больше возможностей для достижения этой цели.

Запоминание учениками определений, теорем, правил и умение пользоваться ими на практике происходит в процессе решения соответствующих задач и упражнений.

Поэтому одним из самых важных аспектов обучения математике в средней школе, несомненно является работа над задачей. Несмотря на изменяющиеся стандарты математического образования, решение задач было и остается основным фактором формирования важнейших качеств личности ученика.

Математическое знание в отличие от других наук, может быть проверено самим учащимся, причём эта проверка носит для него творческий характер, показывающий его уровень понимания темы.

Рассмотрим далее теорему об отрезках касательных к окружности и её применение к решению планиметрических задач.

Основнаятеорема. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности [2].

Т.е AB=AC; ∠1=∠2 (рис.1).

Задача 1. Катеты прямоугольного треугольника равны a и b, гипотенуза с. Найти радиус вписанной окружности (рис.2).

Обозначим точки касания вписанной окружности со сторонами треугольника М, N, P.

О — центр окружности.

По указанной выше теореме AM=AN, BN=BP, CM=CP и четырехугольник СMOP — квадрат.

Пусть AM=AN=x, BN=BP=y, CM=CP=r.

Составим систему 3 уравнений:

Сложив два последних уравнения,

x+y+2r=a+b или c+2r=a+b. Отсюда r=(a+b−c):2. Задача решена.

Преобразовав последнее равенство, получим ещё одну полезную формулу:

Радиус вписанной окружности равен разности полупериметра и гипотенузы.

Задача 2. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 и 12. Найти катеты треугольника (рис.3).

AK=12, BK=5. Пусть M и N — точки касания окружности с катетами BC и AC.

BM=BK=5, AN=AK=12, CN=CM=r, тогда AC=12+r, BC=5+r, AB=12+5=17.

По теореме Пифагора (5+r) 2 +(12+r) 2 =289. Решая уравнение, получаем r₁=3, r₂=−20.

Понятно, что интересующий нас ответ r=3, но у пытливого ученика может возникнуть вопрос: а в чем смысл второго корня? Ведь, составляя уравнение, мы поставим перед ним вполне определенную задачу — найти радиус вписанной окружности. Но при составлении уравнения мы запрограммировали определенное условие: найти радиус окружности, которая касается прямых AC, BC и AB и делит отрезок AB на отрезки, равные 5 и 12.

Вот уравнение и выдало нам ещё один радиус, как оказалось вневписанной окружности, для которой все указанные выше условия выполняются, но центр её находится вне треугольника.

Задача 3. Из точки, лежащей вне окружности радиуса 1, проведены к ней две взаимно перпендикулярные касательные MB и MA. Между точками касания A и B на меньшей дуге AB взята произвольная точка С и через неё проведена третья касательная KL, образующая с касательными MA и MB треугольник KLM. Найти его периметр (рис.4).

В самом условии задачи кроется подсказка: положение точки С определено только принадлежностью дуге AB и более никак не уточняется, следует ожидать, что оно и не влияет на ответ, что на самом деле и оказывается:

Задача 4. Равнобедренный треугольник описан около окружности с радиусом, равным 6. К окружности проведена касательная, параллельная основанию, причём длина отрезка касательной, заключенной между боковыми сторонами треугольника равна 8. Найдите основание треугольника (рис.5).

В одном из пособий есть решение этой задачи, с использованием подобия треугольников MBN и ABC, приводящее к квадратному уравнению. Решение задачи с использованием нашей темы выглядит более компактным и изящным.

Обозначим D,E,F и G — точки касания вписанной окружности со сторонами треугольника ABC и отрезком MN. O — центр окружности. NE=NG=4. Соединим точку О с N и C. Получим прямоугольный треугольник ONC, в котором OG — высота.

По теореме о пропорциональных отрезках в прямоугольном треугольнике: OG 2 =NG∙GC и GC=OG 2 :NG=>GC=9 и AC=18.

Задача 5. В трапецию вписана окружность r=6. Точка касания делит нижнее основание трапеции на отрезки 9 и 12. Найти стороны и площадь трапеции (рис.6).

Эта задача похожа на задачу 4.

Дважды применив способ, получаем отрезки CP и CK, из которых складывается верхнее основание, попутно определяются длины боковых сторон и площадь можно определить по формуле S=pr, где p=0,5r, а r нам известно.

Ответ: BC=7, AB=13, CD=15, S=168.

Задача 6. В треугольнике ABC: AB=10, BC=5, CA=6. Точка D лежит на прямой BC так, что BD:DC=1:2. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются отрезка AD в точках E и F. Найти EF.

Из соотношения сторон видно, что треугольник ABC тупоугольный. Рассмотрим два случая.

Случай 1. Точка O находится на отрезке BC (рис.7).

Обозначив точки касания окружностей со сторонами треугольника M,N,P и K и по теореме об отрезках касательных, получаем:

Из уравнения EF=17/3−EF находим EF=17/6.

Случай 2. Точка D находится на прямой BC так, что точка B лежит между точками C и D (рис.8).

В этой части будут рассмотрены задачи, в которых главенствует теорема о пропорциональных отрезках на сторонах угла, которая, как известно обобщает теорему Фалеса и связанные с ней отношения площадей треугольников имеющих: а) равные высоты б) равные основания в) равные углы

Основная теорема. Если стороны угла пересечены параллельными прямыми, то отрезки, отсекаемые ими на одной стороне угла, пропорциональны соответственным отрезкам, отсекаемым ими на другой стороне (рис.9).

Также нам будут полезны следующие утверждения:

• Площади треугольников, имеющих равные высоты относятся как длины оснований;
• Площади треугольников, имеющих равные основания, относятся как длины высот, к ним проведенных;
• Площади треугольников, имеющих по одному равному углу относятся как произведение сторон их образующих;
• Площади подобных фигур относятся как квадрат коэффициента подобия.

Рассмотрим два подхода к решению одной задачи.

Задача 1. В треугольнике ABC на стороне AC взята точка М, такая, что AM=2AC:5, а на стороне BC — точка K, такая, что BK=BC:3. В каком отношении отрезок BM делит отрезок AK.

Из условий задачи следует, что AM:MC=2:3 и BK:KC=1:2.

Самое сложное в подобных задачах — провести нужный отрезок, чтобы использовать вышеуказанную теорему.

В этой задаче это отрезок KL параллельный BM. Тогда BK:KC=ML:LC=1:2, но поскольку в первом отношении на MС приходилось три части, то тогда отрезок ML содержит одну часть и AM:MC=2:1, и вновь по той же теореме AN:NK=AM:MC=1:2.

В пособии [3], решения этой задачи представлялось несколько иначе: все указанные в условии отношения конвертируются с дополнительного построения, которое позволяет переводить их с одной прямой на другую, ей непараллельную (рис.11).

Проведём через точку А прямую параллельную BC и продолжим BM до пересечения с ней в точке L. ΔAMC

Пусть BK=a, тогда BC=3a. AL:BC=AM:MC=>AL=2a. Далее, из подобия треугольников ANL и BNK AN:NK=AL:BK=2a:a=2.

Задача 2. В треугольнике ABC на прямой BC выбрана точка K, что BK:KC=1:2, точка E — середина стороны AB. Прямая CE пересекает отрезок AK в точке P. Найти площадь ΔAEP, если площадь ΔABC равна 120 (рис.12).

Медиана CE делит площадь треугольника ABC на две равные части S_AEC=60. Осталось найти отношение EP:PC, а ещё лучше EP:EC.

Проведём EF параллельно AK. EF — средняя линия треугольника ABK. Следовательно, FK:KC=0,5:2=1:4. Из чего следует: EP:PC=1:4 и EP:EC=1:5, т.е. площадь треугольника AEP равна пятой части площади ΔABC т.е. S_AEP=60:5=12.

Второй случай этой задачи заложен в слове «прямая BC». Согласно которому точку К можно выбрать и за пределами отрезка ВС при том, что условие задачи будет выполнено (рис.13).

Продолжим ВС за точку B и отложим отрезок BK=BC. Условие BK:KC=1:2 выполняется. Решение аналогично. Можно смотреть решение 1-го случая и все повторять здесь:

Проведём EF||AK. В ΔABK EF — средняя линия. Следовательно, FK:KC=0,5:2=1:4 отсюда EP:PC=FK:KC=1:4 или EP:EC=1:3.

Задачи для самостоятельного решения:

1. В равнобедренном треугольнике ABC (AB=BC) на стороне BC выбрана точка D так, что BD:DC=1:4. В каком отношении прямая AD делит высоту BM треугольника ABC.

2. На медиане BD треугольника ABC, площадь которого S выбрана точка E так, что DE=BD:4. Прямая AE пересекает сторону BC в точке F. Найти площадь треугольника AFC.

3. В треугольнике ABC на стороне AB взята точка K так, что AK:BK=1:2, а на стороне BC взята точка L так, что CL:BL=2:1. Пусть Q — точка пересечения прямых AC и CK. Найти площадь треугольника ABC, если площадь ΔBQC=1

4. В треугольнике ABC основание BC=9,5, площадь треугольника 28,5. Окружность, вписанная в треугольник, касается средней линии, параллельной основанию.

• Докажите, что AC+AB=3BC;
• Найдите наименьшую из боковых сторон.

5. В треугольнике ABC AB=BC=10, AC=12. Биссектриса угла BAC пересекает сторону BC точке D и описанную около треугольника окружность в точке P.

• Докажите, что углы ABP и BDP равны;
• Найдите отношение площадей треугольников ADB и BDP.

6. Площадь треугольника ABC равна 10. Площадь треугольника AHB, где H — точка пересечения высот, равна 8. На прямой CH взята точка K так, что треугольник ABK прямоугольный.

• Доказать, что 2 _ABK=∙;
• Найти площадь треугольника.

7. Все четыре треугольника заштрихованные на рис. 14 равновелики.

Рисунок 14.

• Докажите, что все четыре четырехугольника, не заштрихованные на нём равновелики;
• Найдите площадь одного четырехугольника, если площадь одного заштрихованного треугольника равна 1.

8. В треугольнике ABC на сторонах AB,BC и CA отложены соответственно отрезки. AD=AB:3, BE=BC:3, CF=CA:3

• Докажите, что S_AMC=S_ANB=S_BKC, где M=AE∩CD, K=CD∩BF, N=AE∩BF;
• Найдите, какую часть от площади треугольника ABC составляет площадь треугольника MNK.

9. Площадь треугольника ABC равна 12. На прямой AC взята точка D так, что точка С является серединой отрезка AD. Точка K — середина стороны AB, прямая KD пересекает сторону BC в точке L.

• Докажите, что BL:LC=2:1;
• Найдите площадь треугольника BLK.

10. В треугольник ABC вписана окружность. Точка касания окружности стороны AC делит её на отрезки с длинами 6 и 4. Периметр треугольника равен 24. Найти синус угла BAC.

Ответ: 0,6 или 0,8.

11. К окружности, вписанной в треугольник с периметром 18, проведена касательная параллельно основанию треугольника. Отрезок касательной между боковыми сторонами равен 2. Найдите основание треугольника.

Видео:Решаем геометрию ОГЭ по математике 2024! Задание №15.Скачать

Список литературы

1. Корямов А.Г. Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии (многовариантные задачи).
2. www.alexlarin.net – сайт по оказанию информационной поддержки студентам и аби-туриентам при подготовке к ЕГЭ, поступлению в ВУЗы.
3. Шарыгин И.Ф. Решение задач 10 класс. — М.: Просвещение, 1994.
4. Габович И.Г. Алгоритмический подход к решению геометрических задач. — М.: Про-свещение, 1994.
5. Атанасян Л.С. и др. Геометрия 8. Дополнительные главы к школьному учебнику. — М.: Просвещение, 1996.
6. Атанасян Л.С. и др. Геометрия 7-9. М.: Просвещение, 2000.

Завершение формирования электронного архива по направлению «Науки о Земле и энергетика»

• 23 ноября 2020

Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.

Соучредители СМИ: Долганов А.А., Майоров Е.В.

📽️ Видео

ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ПОДОБНЫЕ ТРЕУГОЛЬНИКИСкачать

В каком отношении делит сторону BC треугольника ABC прямая, проходящая через A?Скачать

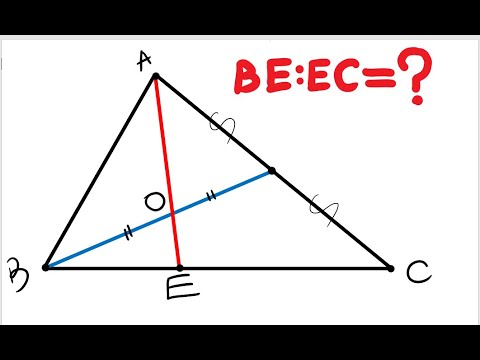
Задание 3 ЕГЭ по математике. Урок 41Скачать

ОГЭ 2024 Ященко 3 вариант ФИПИ школе полный разбор!Скачать

№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

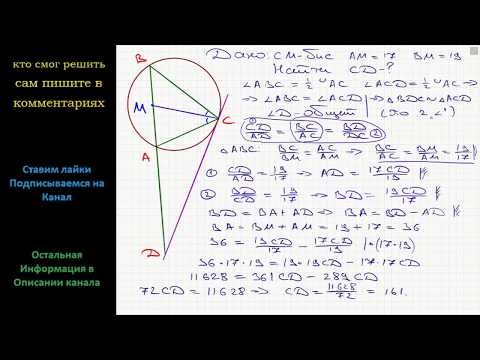
Геометрия Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 17 и MB = 19. КасательнаяСкачать

В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

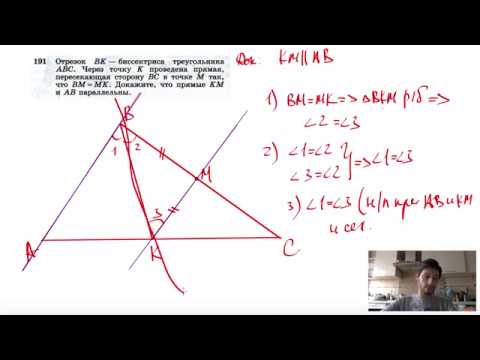
№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

№384. Через середину М стороны АВ треугольника ABC проведена прямая,Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№241. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВСкачать

Геометрия Биссектриса BD треугольника ABC делит сторону AC на отрезки AD и DC длины которыхСкачать

№31. Плоскость α параллельна стороне ВС треугольника ABC и проходит черезСкачать