Поток вектора смещения через поверхность сферы (5 видео)

Теорема Гаусса в интегральной форме

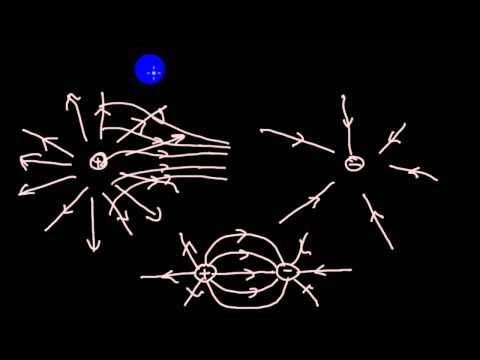
Для формулировки теоремы найдем сначала поток вектора напряженности электрического поля через сферу для поля точечного заряда (рис. 16.2). На поверхности сферы из соображений симметрии поле постоянно по модулю и направлено перпендикулярно поверхности. Из формулы (15.5) для поля точечного заряда имеем

Отсюда поток вектора напряженности электрического поля равен

Если заряд подвинуть внутри сферы или деформировать сферу в эллипс, то, очевидно, величина потока вектора напряженности электрического поля, определяемая количеством проходящих через поверхность силовых линий, остается неизменной.

Несколько сложней ситуация, когда рельеф замкнутой поверхности более сложный и силовая линия может протыкать ее несколько раз. Тем нс менее поток и в этом случае неизменен — благодаря нечетному числу прохождений силовой линии через поверхность. При этом прохождение внутрь поверхности компенсируется прохождением наружу. Так, на рис. 16.3 некоторые силовые линии проходят через поверхность трижды — дважды наружу (положительный поток) и один раз внутрь (отрицательный поток). В результате суммарный поток соответствует одному прохождению силовой линии и определяется формулой (16.6).

Аналогично, если заряд находится вне замкнутой поверхности, то поток — благодаря четному числу прохождений силовой линии через поверхность — равен нулю (рис. 16.4). В результате такого анализа следует важный вывод: поток определяется только зарядом внутри замкнутой поверхности.

Рис. 163 Рис. 16.4

Если внутри замкнутой поверхности находятся N зарядов, то суммарное поле и поток определяются принципом суперпозиции и вывод сохраняется:

Дадим теперь в соответствии с формулами (16.2) и (16.7) окончательную формулировку теоремы Гаусса.

Теорема Гаусса для электрического поля в вакууме: поток вектора напряженности электрического поля через любую замкнутую поверхность равен сумме зарядов, находящихся внутри этой поверхности, деленной на с₀:

Теорема Гаусса позволяет рассчитать электрические поля заряженных тел различной конфигурации. Искусство применения теоремы Гаусса состоит в том, чтобы для данного заряженного тела подобрать удобную замкнутую гауссову поверхность, для которой из соображений симметрии просто вычислить интеграл (16.8). Рассмотрим несколько важнейших примеров.

Содержание

Теорема Гаусса в интегральной форме
Теорема Гаусса в интегральной форме
Поток вектора смещения через поверхность сферы
📺 Видео

Видео:Билет №02 "Теорема Гаусса"Скачать

Теорема Гаусса в интегральной форме

Видео:Применение теоремы Гаусса-Остроградского. Напряжённость поля пластины, сферы и шара.Скачать

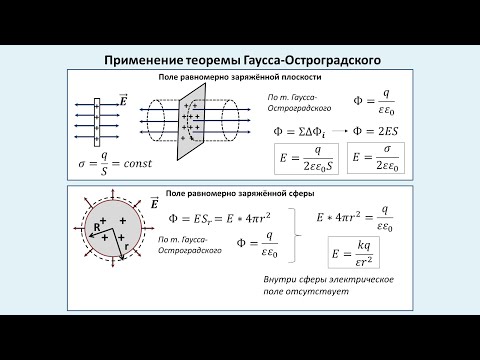
Теорема Гаусса в интегральной форме

Интегральная форма теоремы Гаусса. Поток вектора электрического смещения через замкнутую поверхность, окружающую конкретный объем, равен алгебраической сумме свободных зарядов на этой поверхности. (13.16)

Поскольку SD = eoerE, теорема Гаусса для однородных и изотропных сред имеет вид (5Åds-, (13.17) J «o *), то есть замкнутая поверхность представляет собой

сумму свободных зарядов на этой поверхности. Людмила Фирмаль

В отличие от теоремы Гаусса (13.17), равной произведенному на eoeg произведению, которое в обоих случаях используется для записи, поток вектора E через замкнутую поверхность является суммой свободных зарядов.

Мало того, что он создается суммой объединенных зарядов на поверхности (связь), замкнутая поверхность равна алгебраической сумме связанных зарядов внутри этой поверхности, взятой с противоположным знаком.

Напомним, что ka и вакуум равны модулю вектора поляризации, на рисунках 402 и b показано положение диполя в поляризованном диэлектрике длиной L, сечение S. Совмещенный заряд находится на обоих концах диэлектрика.

Образуются на их поверхности Плотность обозначена o. Длинные положительные и отрицательные заряды взаимно компенсируются, поэтому заряд os концентрируется на обоих концах, 402, b, длина L * диполя.

учитывая поляризационный диэлектрик Людмила Фирмаль

Электрический момент всего диэлектрика длиной L равен usL, поэтому электрический момент объема диэлектрического блока равен, а плотность связанных зарядов на обоих концах поляризованного диэлектрика равна модулю вектора поляризации P. (Вектор P перпендикулярен ребру.)

Взгляните на диаграмму: 402, c, которая показывает свободный положительный заряд, который вызвал поляризацию окружающего диэлектрика. Рассчитайте некомпенсированный заряд связи, который упал внутри. Некомпенсированный заряд связи — это заряд диполя, который пересекает поверхность $.

Поскольку их поверхностная плотность равна ct, — (f ods— $ Pds, вперед, теорема Гаусса (Уравнение 13.16 или U ^ fx — электростатическое поле

Обратите внимание, что это также относится к определенным условиям и к переменным электромагнитным полям, где точка, где требуется растянуть расстояние от заряда, генерирующего электромагнитное поле, намного короче электромагнитной длины (подробности) (Подробнее см. § 481.) D.

Максвелл расширил теорему Гаусса на переменные электромагнитные поля: уравнения Максвелла (13.17) и (13.17x) имеют разные правые части, или ИЛИ, поэтому уравнение (13.16) имеет вид

Следовательно, eo fÅds Yasvob cfe -g Chsvob 4 и simplicity все еще являются замкнутой поверхностью для зарядов, расположенных в замкнутой поверхности через эту точку, поэтому вся эта поверхность

Если условие равенства точек (симметричное) может быть реализовано, оно используется для определения интенсивности и электрического смещения в любой точке поля. Такие поверхности обычно представляют собой сферы (если заряд представляет собой точку) или стороны цилиндра (если заряд является «линейным»).

Кроме того, из-за симметричного положения всех точек на поверхности относительно заряда значения напряженности поля в разных точках на этой поверхности будут одинаковыми.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Поток вектора смещения через поверхность сферы

отсюда можно записать:

где P = . — вектор поляризации; . — диэлектрическая восприимчивость среды, характеризующая поляризацию единичного объема среды.

Таким образом, вектор D есть сумма (линейная комбинация) двух векторов различной природы: E — главной характеристики поля и P — поляризации среды.

В СИ . т.е. это заряд, протекающий через единицу поверхности.

Для точечного заряда в вакууме .

Для D имеет место принцип суперпозиции, как и для E , т.е.

1.4.4. Поток вектора электрического смещения. Теорема Остроградского-Гаусса для D

Аналогично потоку для вектора E . можно ввести понятие потока для вектора D (Φ_D). Пусть произвольную площадку S пересекают линии вектора электрического смещения D под углом α к нормали n (рис. 1.4.10):

В однородном электростатическом поле Φ_D = DS cos α = D_nS.

Теорему Остроградского — Гаусса для вектора D получим из теоремы Остроградского — Гаусса для вектора E: