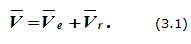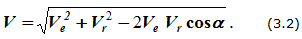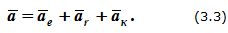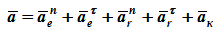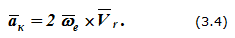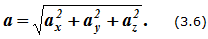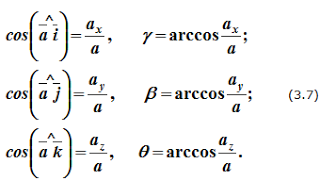Теорема о векторе скорости

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Теорема

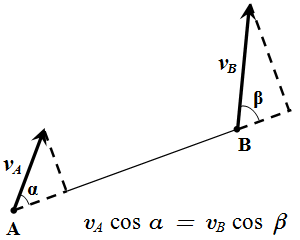
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.
v_A cos α = v_B cos β .

Доказательство

Выберем прямоугольную неподвижную систему координат Oxyz . Возьмем две произвольные точки твердого тела A и B . Пусть ( x_A, y_A, z_A ) и ( x_B, y_B, z_B ) – координаты этих точек. При движении твердого тела они являются функциями от времени t . Дифференцируя по времени, получаем проекции скоростей точек.
, .

Воспользуемся тем, что при движении твердого тела, расстояние | AB | между точками остается постоянным, то есть не зависит от времени t . Также постоянным является квадрат расстояния
.
Продифференцируем это уравнение по времени t , применяя правило дифференцирования сложной функции.

Сократим на 2 .
(1)

Введем вектор
.
Тогда уравнение (1) можно представить в виде скалярного произведения векторов.
(2)
Выполняем преобразования.
;
(3) .
По свойству скалярного произведения
,
.
Подставляем в (3) и сокращаем на | AB | .
;

Что и требовалось доказать.

Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Относительная скорость

Рассмотрим движение точки B относительно точки A . Введем относительную скорость точки B относительно A .

Тогда уравнение (2) можно переписать в виде
.

То есть относительная скорость перпендикулярна вектору , проведенному из точки A в точку B . Поскольку точка B взята произвольным образом, то относительная скорость любой точки твердого тела перпендикулярна радиус вектору, проведенному из точки A . То есть относительно точки A тело совершает вращательное движение. Относительная скорость точек тела определяется по формуле для вращательного движения
.

Точку A , относительно которой рассматривают движение, часто называют полюсом.

Абсолютную скорость точки B относительно неподвижной системы координат можно записать в следующем виде:
.
Она равна сумме скорости поступательного движения произвольной точки A (полюса) и скорости вращательного движения относительно полюса A .

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Пример решения задачи

Колеса 1 и 2 с радиусами R ₁ = 0,15 м и R ₂ = 0,3 м , соответственно, соединены шарнирами со стержнем 3 длины | AB | = 0,5 м . Колесо 1 вращается с угловой скоростью ω ₁ = 1 рад/с . Для изображенного на рисунке положения механизма, определить угловую скорость ω ₂ колеса 2. Принять L = 0,3 м .

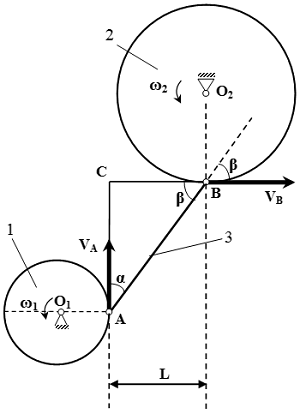
Рисунок к решению задачи

Точка A движется по окружности радиуса R ₁ вокруг центра вращения O ₁ . Скорость точки A определяется по формуле
V_A = ω ₁ R ₁ .
Вектор направлен вертикально (перпендикулярно O ₁ A ).

Точка B движется по окружности радиуса R ₂ вокруг центра вращения O ₂ . Скорость точки B определяется по формуле
V_B = ω ₂ R ₂ .
Отсюда
.
Вектор направлен горизонтально (перпендикулярно O ₂ B ).

Строим прямоугольный треугольник ABC . Применяем теорему Пифагора.
(м)
Косинус угла между вектором скорости и прямой AB , в направлении вектора , равен
.
Косинус угла между вектором скорости и прямой AB , в направлении вектора , равен
.

По теореме о проекциях скоростей двух точек твердого тела на прямую имеем:
V_A cos α = V_B cos β .
Отсюда
.

Находим угловую скорость колеса 2.
рад/с .

Автор: Олег Одинцов . Опубликовано: 07-10-2015

Видео:Физика | Ликбез по векторамСкачать

iSopromat.ru

Рассмотрим определение величины и направления скоростей и ускорений точек при сложном движении. Кориолисово ускорение, правило векторного произведения и правило Жуковского.

Теоремы о скоростях и ускорениях точек в сложном движении подробно изложены в учебниках по теоретической механике.

Абсолютная скорость точки при сложном движении определяется как геометрическая сумма переносной и относительной скоростей:

Каждое слагаемое в этой формуле определяется независимо друг от друга, исходя из соответствующего закона движения. В примере на рисунке 3.2 относительная скорость V_r определяется с учетом закона движения точки по оси Oy.

Переносная скорость определится как скорость точки M при вращении вместе с квадратом вокруг оси его вращения. Величина абсолютной скорости может быть определена с помощью теоремы косинусов:

Для определения вектора абсолютной скорости можно равенство (3.1) спроецировать на выбранные оси координат, найти проекции абсолютной скорости, её величину и направляющие косинусы, то есть определить углы, которые вектор скорости составляет с выбранными осями.

Ускорение точки при сложном движении определяется как сума трех ускорений: переносного, относительного и кориолисова (поворотного):

Первые два слагаемые этой формулы определяются из соответствующих законов переносного и относительного движений. В случае неравномерных криволинейных движений эта формула имеет вид

Величина этого ускорения

где α — угол между векторами переносной угловой и линейной относительной скоростями.

Направление кориолисова ускорения определяется двумя правилами:

Видео:Урок 19. Относительность движения. Формула сложения скоростей.Скачать

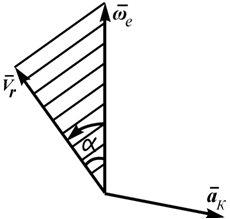
1. Правило векторного произведения при сложном движении

Согласно этому правилу вектор кориолисова ускорения перпендикулярен векторам ω_e и V_r (или плоскости, проходящей через эти вектора, проведенные из одной точки). Направлен вектор a_K так, что если смотреть ему навстречу, то кратчайший поворот вектора ω_e до совмещения с вектором V_r происходит против хода часовой стрелки (рисунок 3.3).

Видео:Мгновенный центр скоростейСкачать

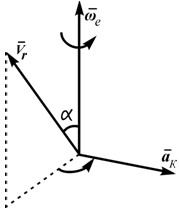
2. Правило Жуковского при сложном движении

Для определения направления кориолисова ускорения при сложном движении нужно спроецировать вектор относительной скорости в плоскость, перпендикулярную вектору переносной угловой скорости и полученную проекцию повернуть на в сторону переносного вращения (рисунок 3.4).

Из формулы (3.5) видно, что кориолисово ускорение равно нулю, если

• равна нулю относительная скорость;
• переносное движение — поступательное ( ω_e=0);
• угол между ω_e и V_r равен 0 o или 180 o (вектор V_r параллелен оси переносного вращения).

Абсолютное ускорение точки при сложном движении определяется по аналогии с определением её скорости. Формула (3.3) проецируется на выбранные оси координат, и находятся проекции абсолютного ускорения на эти оси: a_x, a_y, a_z. Величина ускорения определяется по формуле:

Направление вектора абсолютного ускорения определяется с помощью направляющих косинусов, то есть определяются углы, которые вектор ускорения составляет с осями координат:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Определение скоростей точек плоской фигуры

Напомним, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения вместе с полюсом и вращательного движения вокруг полюса.

В соответствии с этим скорость произвольной точки М плоской фигуры геометрически складывается из скорости какой-нибудь точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса, т. е.

При этом скорость V_MA определяется как скорость точки М при вращении тела вокруг неподвижной оси, проходящей через точку А перпендикулярно плоскости движения (см. § 7.2), т. е.

Таким образом, если известны скорость полюса V_А и угловая скорость тела со, то

скорость любой точки М тела определяется в соответствии с равенством (8.2), диагональю параллелсгграмма, построенного на векторах V_A и V_MA, как на сторонах (рис. 8.3), а модуль скорости V_M вычисляется по формуле

где у — угол между векторами V_A и V_MA

Задача 8.1. Колесо катится по неподвижной поверхности без скольжения (рис. 8.4, а). Найти скорость точек К и D колеса, если известны скорость V_c центра С колеса, радиус R колеса, расстояние КС = b и угол а.

Решение. 1. Рассматриваемое движение колеса является плоскопараллельным. Приняв точку С за полюс (так как ее скорость известна), в соответствии с общим равенством (8.2), для точки К можем записать

Однако нет возможности определить значение V_KC, так как неизвестна угловая скорость со.

Для определения со рассмотрим скорость другой точки, а именно точки Р касания колеса о неподвижную поверхность (рис. 8.4, б). Для этой точки можно написать равенство

Особенностью точки Р является то обстоятельство, что в данный момент времени V_p— 0, так как колесо катится без скольжения. Тогда равенство (б) принимает вид

Отсюда следует: 1) векторы скоростей V_PC и V_c должны быть направлены в противоположные стороны; 2) из равенства модулей V_PC — V_c получаем ыРС= V_c, отсюда найдем со = V_c/PC= V_c/R. В соответствии с направлением вектора V_PC определяем направление дуговой стрелки со и показываем ее на чертеже (рис. 8.4, б).

Теперь возвращаемся к определению V_K по равенству (а). Находим

Vкс = о КС — V^b/R. Зная направление угловой скорости со, изображаем вектор V_KC перпендикулярно отрезку КС и выполняем построение параллелограмма на векторах V_c и V_KC (рис. 8.4, в). Так как в данном случае V_c и V_KC взаимно перпендикулярны, окончательно находим

2. Скорость точки D на ободе колеса определим из равенства V_D = V_C + V_DC. Так как численно V_DC— соR — V_c, то параллелограмм, построенный на векторах V_c и V_DC, будет ромбом. Угол между V_c и V_DC равен 2а. Определив V_D как длину соответствующей диагонали ромба, получим

Теорема о проекциях скоростей двух точек твердого тела

Согласно равенству (8.2) для двух_ произвольных точек А и В твердого тела справедливо равенство V_B =V_A +V_BA, в соответствии с которым выполним построение, показанное на рис. 8.5. Проецируя это равенство на ось Az, направленную по А В, получим Ум + V_BAz. Учитывая, что вектор V_BA перпендикулярен прямой

Этот результат и выражает теорему: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.

Отметим, что равенство (8.5) математически отражает то обстоятельство, что тело рассматривается как абсолютно твердое и расстояние между точками А и В не изменяется. Поэтому равенство (8.5) выполняется не только при плоскопараллельном, но и при любом движении твердого тела.

Задача 8.2. Ползуны А и В, соединенные стержнем с шарнирами на концах, перемешаются по взаимно перпендикулярным направляющим в плоскости чертежа (рис. 8.6, а). Определить при данном угле а скорость точки В, если известна скорость V_A.

Решение. Проведем ось х через точки А и В. Зная направление V_A,

находим проекцию этого вектора на прямую АВ: V_Ax — V_A cos а (на рис. 8.6, б это будет отрезок Аа). Далее на чертеже от точки В откладываем ВЬ — Аа (так как отрезок Аа расположен на оси х вправо от точки А, то и отрезок ВЬ откладываем от точки В по оси х вправо). Восставляя в точке Ь перпендикуляр к прямой АВ, находим точку конца вектора V_B.

Согласно теореме о проекциях V_A cos а = K^cosp. Отсюда (учтя, что Р = 90° — а) окончательно получим V_B = V_A cos a/cos(90° — a) или V_B = = V_A ctg a.

Определение скоростей точек с помощью мгновенного центра скоростей

Для определения скоростей точек плоской фигуры выберем в качестве полюса какую-либо точку Р. Тогда, согласно формуле

(8.2), скорость произвольной точки М определяется как сумма двух векторов:

Если бы скорость полюса Р в данный момент времени была равна нулю, то правая часть этого равенства была бы представлена одним слагаемым У_МР и скорость любой точки определялась бы как скорость точки М тела при вращении его вокруг неподвижного полюса Р.

Следовательно, если выбрать в качестве полюса точку Р, скорость которой в данный момент времени равна нулю, то модули скоростей всех точек фигуры будут пропорциональны их расстояниям до полюса Р, а направления векторов скоростей всех точек будут перпендикулярны прямым, соединяющим рассматриваемую точку и полюс Р. Естественно, что расчет по формулам (8.6) значительно проще расчета по общей формуле (8.2).

Точка плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС). Легко убедиться, что если фигура движется непоступательно, то такая точка в каждый момент времени существует и при том единственная. Отметим, что мгновенный центр скоростей может быть расположен как на самой фигуре, так и на ее мысленном продолжении.

Рассмотрим способы определения положения мгновенного центра скоростей.

1. Пусть в момент времени t jum плоской фигуры известны ее угловая скорость со и скорость V_A какой-нибудь ее точки А (рис. 8.7, а). Тогда, выбирая точку А в качестве полюса,_скорость_иско- мой нами точки Р можно определить по формуле V_p = V_A + Vp_A—

Задача состоит в том^чтобы найти такую точку Р, у которой V_P =0, значит, для нее V_A +У_РЛ =0 и отсюда У_РА = -У_А. Следовательно, для точки Р скорость У_РА, которую точка Р получает при вращении фигуры вокруг полюса А, и скорость У_А полюса А равны по модулю (У_РА= У_А) или озАР= У_А и противоположны по направлению. Кроме того, точка Р должна лежать на перпендикуляре к вектору У_А. Определение положения точки Р осуществляется таким построением: из точки А (рис. 8.7, б) восставим перпендикуляр к вектору У_А и отложим на нем расстояние АР = У_А/со в ту сторону от точки А, куда «покажет» вектор У_А, если его повернуть на 90° в направлении дуговой стрелки со.

Мгновенный центр скоростей является единственной точкой плоской фигуры, скорость которой в данный момент времени равна нулю.

В другой момент времени мгновенным центром скоростей может быть уже другая точка плоской фигуры.

2. Пусть известны направления скоростей V_A и У_в (рис. 8.8, а) двух точек А и В плоской фигуры (причем векторы скоростей этих точек непараллельны), или известны элементарные перемещения этих точек. Мгновенный центр скоростей будет находиться в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к элементарным перемещениям точек). Такое построение выполнено на рис. 8.8, б. Оно основано на том, что для любых точек А и В фигуры применимы положения (8.6):

Из этих равенств следует, что

Зная положение МЦС и угловую скорость тела, применив формулы (8.6), легко определить скорость любой точки этого тела. На- пример^для точки К (см. рис. 8.8, б) модуль скорость V_K=coКР, вектор У_к направлен перпендикулярно прямой КР в соответствии с

направлением дуговой стрелки ю.

Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как будто эта фигура вращается вокруг мгновенного центра скоростей.

3. Если скорости точек А и В плоской фигуры параллельны друг другу, то возможны три варианта, которые изображены на рис. 8.9. Для случаев, когда прямая АВ перпендикулярна векторам V_А и V_B (рис. 8.9, а, б), построения основываются на пропорции (8.7).

Если скорости точек Ли В параллельны, а прямая AB_nt перпендикулярна V_А (рис. 8.9, в), то перпендикуляры к У_А и V_B параллельны и мгновенный центр скоростей находится в бесконечности (АР= оо); угловая скорость вращения фигуры со = VJAP = V_A/cc = 0. В этом случае скорости всех точек фигуры в данный момент времени равны друг другу, т. е. фигура имеет распределение скоростей как при поступательном движении. Такое состояние движения тела называют мгновенно поступательным. Отметим, что в этом состоянии ускорения всех точек тела не будут одинаковыми.

4. Если плоское движение тела осуществляется путем его качения без скольжения по неподвижной поверхности (рис. 8.10), то точка касания Р будет являться мгновенным центром скоростей (см. задачу 8.1).

Задача 8.3. Плоский механизм состоит из стержней 7, 2, 3, 4 и ползуна В (рис. 8.11), соединенных друг с другом и с неподвижными опорами 0_< и 0₂ шарнирами; точка D находится в середине стержня АВ. Длины стержней: /₂ =0,4 м, /₂ = 1,2 м, /₃ = 0,7 м, /₄ = 0,3 м. Угловая скорость стержня 7 в заданном положении механизма со, = 2 с -1 и направлена против хода часовой стрелки. Определить V_A, V_B, V_D, V_E, oo₂, co₃, to₄ и скорость точки К в середине стержня DE (DK = КЕ).

Решение. В рассматриваемом механизме стержни 7, 4 совершают вращательное движение, ползун В — поступательное, а стержни 2, 3 —

Скорость точки А определим как принадлежащую стержню 7, совершающему вращательное движение:

Рассмотрим движение стержня 2. Скорость точки А определена, а направление скорости точки В обусловлено тем, что она принадлежит одновременно стержню 2 и пол-

зуну, движущемуся вдоль направляющих. Теперь, восставляя из точек А и В перпендикуляры к У_А и направлению движения ползуна В, находим положение точки С₂ — МЦС стержня 2.

По направлению вектора У_А, учитывая, что в рассматриваемом положении механизма стержень 2 вращается вокруг точки С₂, определяем направление угловой скорости со₂ стержня 2 и находим ее числовое значение (о₂ = V_a/AC₂ = 0,8/1,04 = 0,77 с -1 , где АС₂ — АВ sin 60° = 1,04 м (получим при рассмотрении ААС

Теперь определяем числовые значения и направления скоростей точек В и D стержня 2 (так как ABDC₂ равносторонний, то ВС₂ — DC₂ — — 0,6 м):

Рассмотрим движение стержня 3. Скорость точки D известна. Так как точка Е принадлежит одновременно и стержню 4, вращающемуся вокруг оси 0₄, то У_е10₄Е. Тогда, проводя через точки D и Е прямые, перпендикулярные скоростям V_D wV_E, находим положение точки С₃ — МЦС стержня

3. По направлению вектора V_D, глядя из неподвижной точки С₃, определяем направление угловой скорости со₃, а ее числовое значение находим (предварительно определив из AZ)C₃? отрезок Z)C₃ = DEsin 30° = 0,35 м): со₃ = V_d/C₃D= 1,32 с -1 .

Для определения скорости точки К проведем прямую КС₃ и, учитывая, что АР КС₃ равносторонний (КС₃ = 0,35 м), вычислим У_к = Далее, вычислив С₃Е — 0,606 м, определяем У_Е — о₃С₃Е — 0,8 м/с, V_eAC₃E.

Рассмотрим движение стержня_4, вращающегося вокруг оси 0₄. Зная направление и числовое значение V_E, находим направление и значение угловой скорости со₄: со₄ = V_e/0₄E — 2,67 с .

Ответ: V_A = 0,8 м/с, V_B = V_D = 0,462 м/с, V_E= 0,8 м/с, со₂ = 0,77 с» 1 , со₃ = 1,32 с -1 , (о₄ = 2,67 с -1 , направления этих величин показаны на рис. 8.11.

Примечание. В механизме, состоящем из нескольких тел, каждое непоступательно движущееся тело имеет в данный момент времени свой мгновенный центр скоростей и свою угловую скорость.

Задача 8.4. Плоский механизм состоит из стержней 1, 2, 3 и катка, катящегося без скольжения по неподвижной плоскости (рис. 8.12, а). Соединения стержней между собой и стержня 3 к катку в точке D — шарнирные. Длины стержней: 1 _<— 0,4 м, /₂ = 0,6 м, /₃ = 0,8 м. При данных углах а = 60°, В = 30° известны значения и направления угловой скорости со, = = 2 с и скорости центра О катка V₀ = 0,346 м/с, ZABD = 90°. Определить скорость точки В и угловую скорость со₂.

Решение. Механизм имеет две степени свободы (его положение определяется двумя углами а и р, не зависящими друг от друга) и скорость точки В (общей точки стержней 2 и 3) зависит от скоростей точек А и D.

Рассматривая движение стержня /, н аходим направление и значение скорости точки A: V_A = coj/j = 0,8 м/с, V_aAjO_<A.

Рассмотрим движение катка. Его мгновенный центр скоростей расположен в точке Р; тогда V_D найдем из пропорции

Так как ADOP равнобедренный и острые углы в нем равны 30°, то DP— 2 OP cos 30° = ОРл/3. Из равенства (а) находим V_D — 0,6 м/с. Вектор V_D направлен перпендикулярно DP.

Так как точка В принадлежит одновременно стержням АВ и BD, то по теореме о проекциях скоростей должно быть: 1) проекция вектора У_в на прямую А В равна проекции на эту прямую вектора У_А (отрезок Аа на рис. 8.12, а), т. е. У_А cos а = 0,4 м/с; 2) проекция вектора У_в на прямую DB равна проекции на эту прямую вектора У₀ (отрезок Dd на рис. 8.12, а), т. е. У₀ cos у = 0,3 м/с (у = 60°).

Далее решаем графически. Откладываем от точки В в соответствующих направлениях отрезки ВЬ _<= Аа и Bb₂ = Dd. Скорость точки В равна сумме векторов V_B = Bb+ Bbj. Восставляем из точки Ь_< перпендикуляр к ВЬ_Х, а из

точки b₂ — перпендикуляр к ВЬ₂. Точка пересечения этих перпендикуляров определяет конец искомого вектора V_B.

Так как направления отрезков ВЬ и ВЬ₂ взаимно перпендикулярны, то

Определяем со₂. На рис. 8.12, б показан так называемый план скоростей, который графически изображает векторное равенство

где векторы V_A и V_B определены (см. рис. 8.12, а), а направление V_BA перпендикулярно стержню АВ. Из чертежа (рис. 8.12, б) находим

Теперь определяем со₂ = V_ba/AB— 1,66 с -1 (направление со₂ — против хода часовой стрелки).

🔥 Видео

Закон Сложения Скоростей - Относительная скорость / Урок Физики 10 класс / КинематикаСкачать

2.4. Радиус-вектор и вектор перемещенияСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать

Теорема Наполеона и операции над векторамиСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

Урок 222. Поток вектора напряженности электрического поляСкачать

Урок 84. Теорема о движении центра массСкачать

Математика это не ИсламСкачать

✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Скорости точек плоской фигурыСкачать