Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.
Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.
 Вписанный многоугольник | 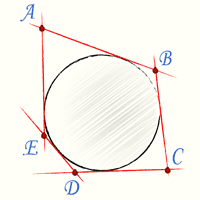 Описанный многоугольник |
Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.
- Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- Геометрический тест: как хорошо вы знаете математику?
- Какой из этих ученых не имеет отношения к геометрии?
- Периметр — это.
- Все фигуры имеют одинаковый периметр. Какая из них имеет наибольшую площадь?
- Какая фигура изображена на картинке?
- Как называется эта геометрическая фигура?
- Какое геометрическое тело изображено на картинке?
- Сумма всех углов треугольника составляет.
- Формула Герона используется для.
- В какую фигуру нельзя вписать окружность?
- Отрезок — это.
- Отношением противолежащего катета к гипотенузе называется.
- Как называется утверждение, требующее доказательства?
- 💥 Видео
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них
Для треугольника всегда возможны и вписанная окружность и описанная окружность.
Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.
Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.
Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрический тест: как хорошо вы знаете математику?
Геометрия — одна из древнейших частей математики, изучающая пространственные отношения и формы тел. Хорошо ли вы слушали своего учителя по этому сложному предмету? Пройдите наш геометрический тест с ответами и узнайте!
Видео:Задача Какая фигура лишняяСкачать
Какой из этих ученых не имеет отношения к геометрии?
Леонардо да Винчи
Видео:Как быстро распределить объекты по окружности в Adobe IllustratorСкачать

Периметр — это.
Численная величина, которая характеризует размер фигуры
Сумма длины всех сторон
Вместимость области пространства
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Все фигуры имеют одинаковый периметр. Какая из них имеет наибольшую площадь?
Видео:Нейрографика. Какие фигуры используем и что они обозначают.Скачать

Какая фигура изображена на картинке?
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как называется эта геометрическая фигура?
Видео:КАК РАСПОЛОЖИТЬ ОБЪЕКТЫ ПО ОКРУЖНОСТИ В ADOBE ILLUSTRATOR. 4 ПРОСТЫХ СПОСОБА!Скачать

Какое геометрическое тело изображено на картинке?
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Сумма всех углов треугольника составляет.
Видео:Урок Illustrator №1 - Создание объемного текста по форме фигурыСкачать

Формула Герона используется для.
Вычисления площади треугольника
Вычисления площади прямоугольника
Вычисления площади ромба
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

В какую фигуру нельзя вписать окружность?
Вопрос 10 из 12
Видео:Как нарисовать ШАР (сфера). Построение , штриховка.Скачать

Отрезок — это.
Линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Часть прямой, которая ограничена двумя точками
Часть прямой, которая имеет начало, но не имеет конца
Вопрос 11 из 12
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Отношением противолежащего катета к гипотенузе называется.
Вопрос 12 из 12
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Как называется утверждение, требующее доказательства?
Поздравляем! Вы закончили проходить геометрический тест! Расскажите друзьям о своем результате!
Русский язык очень богат, красив и сложен. Говорить и писать грамотно по-русски может лишь начитанный и образованный человек. Чтобы проверить твою грамотность, достаточно ответить на несколько наших вопросов. Поехали!
Говорите как native speaker. В этом тесте мы предлагаем вам узнать интересные образные выражения на английском языке, не забывайте — значение идиом всегда в переносном смысле, а не буквальном. Какие из этих английских идиом с цветами вы уже знаете?
Советская школа давала сильные знания в области математики, тем самым развивая логику и мышление у учеников. Как ты считаешь, знаешь ли ты математику так, как знал ее советский девятиклассник? Это несложно проверить, в этом тесте 8 стандартных вопросов для учеников этой параллели времен СССР.
У тебя хорошее воображение? Тогда представь, что мимо тебя по улице идет Эрнест Хемингуэй или Максим Горький. Сделал бы ты с ними селфи или взял бы автограф? Или просто бы прошел мимо, даже не узнав?
Физика – мать всех наук. Почему? Да потому, что всё в мире подчиняется законам этой науки. Знать её рекомендуется именно поэтому. Разбираешься ли ты в ней больше школьника? Предлагаем проверить!
Словарные слова требуют только запоминания или поиска проверочных слов. Лучший способ грамотно писать — много читать или тренироваться, проходя тесты, что и предлагаем сделать вам, чтобы повысить свою письменную грамотность! Проверьте себя и определите, правописание каких слов вам нужно запомнить!
Испытайте свою интуицию и логику — закончите мысль автора! Подумайте или прочувствуйте, какую мысль хотел передать писатель и как может заканчиваться фраза. Надеемся, что ваша догадка будет бодрствовать и обязательно поможет вам успешно пройти тест!
Отвлечься от всего и расшевелить извилины порой очень даже полезно. Поэтому откладывай подальше все гаджеты и проходи наш тест максимально честно!
10 вопросов, ответы на которые не может знать простой житель. Чтобы пройти этот тест на 100%, ты должен быть либо опытным врачом, либо заядлым биологом. Поехали!
В состав Америки входит 50 штатов, каждый из которых имеет свои государственные символы и столицу. Только настоящий гик сможет назвать хотя бы некоторые из них. Не из таких ли ты?
Что нашли под полом Мариинского театра? Для чего придумали пузырчатую пленку? Что такое Кин-дза-дза? Если вы не знаете ответы на эти вопросы, то дальше вам будет очень трудно. Итак, тест для настоящего эрудита. Посмотрим, кто тут самый умный!
Сюжет «Ревизора» Николаю Гоголю был подсказан Александром Пушкиным. История основана на довольно реальных событиях произошедших в Новгородской губернии. Сам Александр Сергеевич тоже пользовался историями своих знакомых. Сюжет «Пиковой дамы» ему подсказал князь Голицын, который крупно проигрался, но смог вернуть свои деньги, поставив по совету бабки на три карты. Сейчас мы рассказали вам только два случая из мира русской литературы, но у нас есть ещё. Предлагаем вам пройти наш тест и проверить свою эрудицию. Удачи!
Слитно, раздельно или через дефис? В этом тесте мы будем распутывать загадочные и капризные наречия, которые начинаются на «по». Загадка их состоит в том, что подобрать правило, которые укажет верный вариант написания, не так-то просто, вот эти наречия и капризничают, то подавай им дефис, а то убери, а то и вовсе слитно пиши! Запоминайте верный вариант написания и проверьте себя!
Приглашаем вас пройти визуальный марафон на знание азиатских столиц. Освежите свои знания — мы уверены, что многие города-столицы у вас «на слуху» и вы назовёте их даже не задумываясь, а если вы не помните или не знаете правильный вариант — действуйте наугад! Дополните свои знания и потренируйте память!
В ходе этого теста вы точно повысите свой культурный уровень и обогатите лексический запас. Проверьте свою память, догадку и, конечно, знания — сможете ли вы правильно подобрать термины к определениям, которые касаются различных сфер деятельности человека (вам также пригодятся знания из спортивной и архитектурной сферы — всё понемногу!)
В школьные годы география для многих была любимым предметом. Ведь узнавать о странах, континентах, природе и климате куда привлекательнее, чем заниматься сухими расчетами по техническим дисциплинам. Давайте проверим, как много знаний у вас сохранилось с тех времен. Предлагаем вам пройти тест по окружающему миру и географии: природные зоны России и мира!
Улучшайте свои знания, постоянно тренируя мозг! В этом тесте мы подготовили для вас несколько вопросов для развития логики, и несколько — для проверки знаний по математике. Насколько хорошо вы помните то, что учили в школе? Какие задачи способен ваш мозг решать сейчас? Проверьте свою память, догадку и силу мышления!
В этом тесте мы попросим вас определить верное написание слов, в которых многие путаются, и вот по какому поводу — согласные «на слух» кажутся то удвоенными, а то и нет! Поможет в этом только справочник — а он не всегда под рукой. Тренируйте свою зрительную память и пишите грамотно!
Обществознание — это первый предмет, который готовит школьников к самостоятельной жизни. Он затрагивает основы общественных наук, необходимых для решения типичных проблем во всех сферах жизни. Пройди тест и проверь, насколько ты подкован в этих вопросах.
Эти стихи мы все учили в школьные годы. Они известны буквально всем. Но помните ли Вы их до сих пор? Ведь мало, кто из нас их повторяет. После школы у многих из нас нет времени, чтобы уделить чтению. Но эти стихи должен знать каждый.
💥 Видео
Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Длина окружности. Математика 6 класс.Скачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать