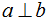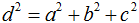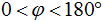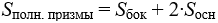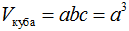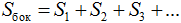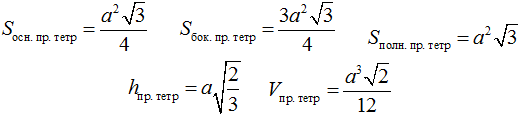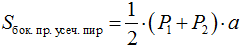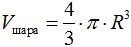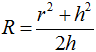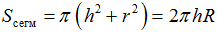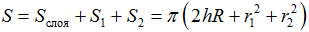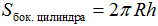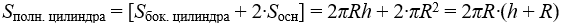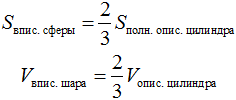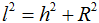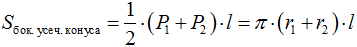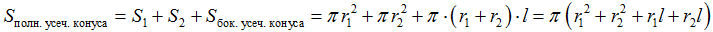Теорема о линии пересечения двух плоскостей содержащих параллельные прямые (8 видео)

Параллельные прямые в пространстве. Параллельность трех прямых

Содержание

Геометрия. 10 класс
Теорема о линии пересечения двух плоскостей содержащих параллельные прямые
Построение сечений в стереометрии
Взаимное расположение прямых и плоскостей в стереометрии
Теорема о трех перпендикулярах
Двугранный угол
Симметрия фигур
Призма
Параллелепипед
Пирамида
Правильная пирамида
Формулы для объема и площади пирамиды
Тетраэдр
Прямоугольная пирамида
Усечённая пирамида
Формулы для усеченной пирамиды
Пирамида и шар (сфера)
Пирамида и конус
Пирамида и цилиндр
Сфера и шар
Многогранники и сфера
Объем и площадь поверхности шара
Шаровой сегмент, слой, сектор
Шаровой сегмент
Шаровой слой
Шаровой сектор
Цилиндр
Цилиндр и призма
Цилиндр и сфера
Объем и площадь боковой и полной поверхностей цилиндра
Конус
Объем и площадь боковой и полной поверхностей конуса
Усеченный конус
Формулы для усеченного конуса:
Конус и сфера
📺 Видео

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы дадим основные определения и теоремы на тему параллельных прямых в пространстве.
В начале урока рассмотрим определение параллельных прямых в пространстве и докажем теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной. Далее докажем лемму о двух параллельных прямых, пересекающих плоскость. И с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №6. Параллельность плоскостей

Перечень вопросов, рассматриваемых в теме

Определение параллельных плоскостей;
Свойства параллельных плоскостей;
Признак параллельности плоскостей.

Глоссарий по теме

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Плоскости, которые не пересекаются, называются параллельными.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.

Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24

Теоретический материал для самостоятельного изучения

Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.

Определение. Плоскости, которые не пересекаются, называются параллельными.

Параллельные плоскости α и β обозначаются α∥β.

Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Пусть α и β — данные плоскости, a₁ и a₂ – пересекающиеся прямые в плоскости α, а b₁ и b₂ соответственно параллельные им прямые в плоскости β.

Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.

Прямая a₁ параллельна прямой b₁, значит она параллельна и самой плоскости β.

Прямая a₂ параллельна прямой b₂, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).

Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a₁ или a₂ пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a₁ или a₂ пересекает плоскость β, чего быть не может, так как прямые a₁ и a₂ параллельны плоскости β.

Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.

Свойства параллельных плоскостей.

Теорема 1. Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.

Пусть α и β — параллельные плоскости, а γ- плоскость, пересекающая их.

Плоскость α пересекается с плоскостью γ по прямой a.

Плоскость β пересекается с плоскостью γ по прямой b.

Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.

Пусть α и β — параллельные плоскости, а a и b – параллельные прямые, пересекающие их.

Через прямые a и b можно провести плоскость — эти прямые параллельны, значит определяют плоскость, причём только одну.

Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.

По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.

Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.

Пусть α||β, a пересекает α в точке А.

Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.

Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.

Теорема 4. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.

Пусть α||β, α и γ пересекаются.

Докажем, что плоскости β и γ пересекаются.

Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.

Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.

Пусть нам даны плоскость α и точка М, ей не принадлежащая.

Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.

В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a₁ и b₁, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a₁ и b₁, обозначим β. На основании признака параллельности плоскостей плоскость β параллельна плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.

Допустим, что через точку M проходит другая плоскость, например β₁, параллельная α.

Так как β₁ пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β₁ пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана.

Рассмотрим несколько примеров на применение данных свойств.

Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.

Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А₁, эти прямые единственным образом определяют плоскость α.

Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .

Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.

Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.

Примеры и разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Три отрезка А₁А₂, В₁В₂ и С₁С₂, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны.

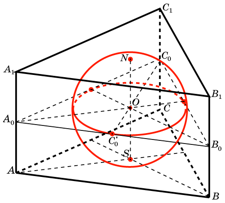
Рассмотрим плоскость, проходящую через прямые А₁А₂ и В₁В₂

(она существует и единственная, т.к. прямые пересекаются).

В этой плоскости лежит четырехугольник А₁В₁А₂В₂, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А₁В₁ и А₂В₂ параллельны.

Аналогично доказывается параллельность В₁С₁ и В₂С₂. Из вышеперечисленного следует, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны по признаку параллельности плоскостей.

Рассмотрим плоскость, проходящую через прямые А₁А₂ и В₁В₂

(она существует и единственная, т.к. прямые пересекаются).

Тип задания: выделение цветом

Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.

Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Теорема о линии пересечения двух плоскостей содержащих параллельные прямые

Некоторые определения:

Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.
Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.
Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.
Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.
Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники.Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы. Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильныеn-угольники.
Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначаетсяS бок ). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначаетсяS полн ).
Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные nграней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.
Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды(обозначается S бок ). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается S полн ).
Правильнаяn-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.
Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).

Аксиомы стереометрии:

Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом стереометрии:

Теорема 1. Через прямую и не лежащую на ней точку проходит единственная плоскость.
Теорема 2. Через две пересекающиеся прямые проходит единственная плоскость.
Теорема 3. Через две параллельные прямые проходит единственная плоскость.

Построение сечений в стереометрии

Для решения задач по стереометрии остро необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба, призмы) некоторой плоскостью. Дадим несколько определений, поясняющих, что такое сечение:

Секущей плоскостью пирамиды (призмы, параллелепипеда, куба) называется такая плоскость, по обе стороны от которой есть точки данной пирамиды (призмы, параллелепипеда, куба).
Сечением пирамиды (призмы, параллелепипеда, куба) называется фигура, состоящая из всех точек, которые являются общими для пирамиды (призмы, параллелепипеда, куба) и секущей плоскости.
Секущая плоскость пересекает грани пирамиды (параллелепипеда, призмы, куба) по отрезкам, поэтомусечение есть многоугольник, лежащий в секущей плоскости, сторонами которого являются указанные отрезки.

Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани. Заметим, что последовательность построения вершин и сторон сечения не существенна. В основе построения сечений многогранников лежит две задачи на построение:

Линии пересечения двух плоскостей.

Для построения прямой, по которой пересекаются некоторые две плоскости α и β (например, секущая плоскость и плоскость грани многогранника), нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей α и β.

Точки пересечения прямой и плоскости.

Для построения точки пересечения прямой l и плоскости α нужно построить точку пересечения прямой l и прямойl 1 , по которой пересекаются плоскость α и любая плоскость, содержащая прямую l.

Взаимное расположение прямых и плоскостей в стереометрии

Определение: В ходе решения задач по стереометрии две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Если прямые а и b, либо AB и CDпараллельны, то пишут:

Несколько теорем:

Теорема 1. Через любую точку пространства, не лежащую на данной прямой, проходит единственная прямая, параллельная данной прямой.
Теорема 2. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Теорема 3 (признак параллельности прямых). Если две прямые параллельны третьей прямой, то они параллельны между собой.
Теорема 4 (о точке пересечения диагоналей параллелепипеда). Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Возможны три случая взаимного расположения прямой и плоскости в стереометрии:

Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).
Прямая и плоскость пересекаются (имеют единственную общую точку).
Прямая и плоскость не имеют ни одной общей точки.

Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямаяа параллельна плоскости β, то пишут:

Теоремы:

Теорема 1 (признак параллельности прямой и плоскости). Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Теорема 2. Если плоскость (на рисунке – α) проходит через прямую (на рисунке – с), параллельную другой плоскости (на рисунке – β), и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке – d) параллельна данной прямой:

Если две различные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны. Однако, в пространстве (т.е. в стереометрии) возможен и третий случай, когда не существует плоскости, в которой лежат две прямые (при этом они и не пересекаются, и не параллельны).

Определение: Две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.

Теоремы:

Теорема 1 (признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.
Теорема 2. Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой.

Теперь введем понятие угла между скрещивающимися прямыми. Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O в пространстве и проведем через нее прямые a 1 и b 1 , параллельные прямым a иb соответственно. Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a 1 и b 1 .

Однако на практике точку O чаще выбирают так, чтобы она принадлежала одной из прямых. Это обычно не только элементарно удобнее, но и рациональнее и правильнее с точки зрения построения чертежа и решения задачи. Поэтому для угла между скрещивающимися прямыми дадим такое определение:

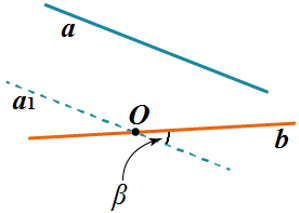
Определение: Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O на одной из них (в нашем случае, на прямой b) и проведем через неё прямую параллельную другой из них (в нашем случае a 1 параллельна a). Углом между скрещивающимися прямыми a и b называется угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a 1 и b).

Определение: Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90°. Перпендикулярными могут быть как скрещивающиеся прямые, так и прямые лежащие и пересекающиеся в одной плоскости. Если прямая a перпендикулярна прямой b, то пишут:

Определение: Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек. Если две плоскости α и β параллельны, то, как обычно, пишут:

Теоремы:

Теорема 1 (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Теорема 2 (о свойстве противолежащих граней параллелепипеда). Противолежащие грани параллелепипеда лежат в параллельных плоскостях.
Теорема 3 (о прямых пересечения двух параллельных плоскостей третьей плоскостью). Если две параллельные плоскости пересечены третьей, то прямые их пересечения параллельны между собой.
Теорема 4. Отрезки параллельных прямых, расположенные между параллельными плоскостями, равны.
Теорема 5 (о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку вне ее). Через точку, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной.

Определение: Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Если прямая a перпендикулярна плоскости β, то пишут, как обычно:

Теоремы:

Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.
Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
Теорема 3 (о параллельности прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.
Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Теорема 5 (о плоскости, проходящей через данную точку и перпендикулярной данной прямой). Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.
Теорема 6 (о прямой, проходящей через данную точку и перпендикулярной данной плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.
Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину:

Следствие: Все четыре диагонали прямоугольного параллелепипеда равны между собой.

Теорема о трех перпендикулярах

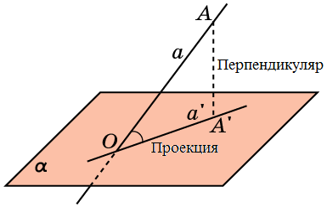
Пусть точка А не лежит на плоскости α. Проведем через точку А прямую, перпендикулярную плоскости α, и обозначим буквой О точку пересечения этой прямой с плоскостью α. Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок АО, точка О называется основанием перпендикуляра. Если АО – перпендикуляр к плоскости α, а М – произвольная точка этой плоскости, отличная от точки О, то отрезок АМ называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок ОМ – ортогональная проекция (или, короче, проекция) наклонной АМ на плоскость α. Теперь приведем теорему, которая играет важную роль при решении многих задач.

Теорема 1 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной. Верно и обратное утверждение:

Теорема 2 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость. Данные теоремы, для обозначений с чертежа выше можно кратко сформулировать так:

Теорема: Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:

две наклонные, имеющие равные проекции, равны;
из двух наклонных больше та, проекция которой больше.

Определения расстояний объектами в пространстве:

Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к данной плоскости.
Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.
Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.

Определение: В стереометрии ортогональной проекцией прямой a на плоскость α называется проекция этой прямой на плоскость α в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости α.

Замечание: Как видно из предыдущего определения, проекций бывает много. Другие (кроме ортогональной) проекции прямой на плоскость можно построить если прямая определяющая направление проецирования будет не перпендикулярна плоскости. Однако, именно ортогональную проекцию прямой на плоскость в будущем мы будем встречать в задачах. А называть ортогональную проекцию будем просто проекцией (как на чертеже).

Определение: Углом между прямой, не перпендикулярной плоскости, и этой плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость (угол АОА’ на чертеже выше).

Теорема: Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.

Двугранный угол

Определения:

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.

Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°). В дальнейшем, при решении задач по стереометрии, под двугранным углом будем понимать всегда тот линейный угол, градусная мера которого удовлетворяет условию:

Определения:

Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.
Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.
Две плоскости называются перпендикулярными, если угол между ними равен 90°.

Теоремы:

Теорема 1 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема 2. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.

Симметрия фигур

Определения:

Точки M и M 1 называются симметричными относительно точки O, если O является серединой отрезка MM 1 .
Точки M и M 1 называются симметричными относительно прямой l, если прямая l проходит через середину отрезка MM 1 и перпендикулярна ему.
Точки M и M 1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка MM 1 и перпендикулярна этому отрезку.
Точка O (прямая l, плоскость α) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки O (прямой l, плоскости α) некоторой точке этой же фигуры.
Выпуклый многогранник называется правильным, если все его грани – равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Призма

Определения:

Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
Боковая поверхность – объединение боковых граней.
Полная поверхность – объединение оснований и боковой поверхности.
Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые ребра призмы параллельны и равны.
Объём призмы равен произведению её высоты на площадь основания:

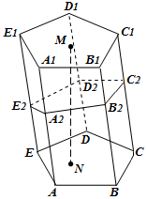
где: S осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A 2 B 2 C 2 D 2 E 2 ).
Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: S сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA 1 или BB 1 и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: P сеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: P осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S осн ∙h = S осн ∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:

Основания правильной призмы являются правильными многоугольниками.
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны между собой.
Правильная призма является прямой.

Видео:Параллельность прямых. 10 класс.Скачать

Параллелепипед

Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.

Другие свойства и определения:

Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро – смежными.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.
Параллелепипед имеет шесть граней и все они – параллелограммы.
Противоположные грани параллелепипеда попарно равны и параллельны.
У параллелепипеда четыре диагонали; они все пересекаются в одной точке, и каждая из них делится этой точкой пополам.
Если четыре боковые грани параллелепипеда – прямоугольники (а основания – произвольные параллелограммы), то он называется прямым (в этом случае, как и у прямой призмы, все боковые ребра перпендикулярны основаниям). Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.
Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.
Объем прямого или наклонного параллелепипеда рассчитывается по общей формуле для объема призмы, т.е. равен произведению площади основания параллелепипеда на его высоту (V = S осн ∙h).
Прямой параллелепипед, у которого все шесть граней – прямоугольники (т.е. кроме боковых граней еще и основания являются прямоугольниками), называется прямоугольным. Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:
- Диагональ прямоугольного параллелепипедаd и его рёбра a, b, c связаны соотношением:

- Из общей формулы для объема призмы можно получить следующую формулу для объема прямоугольного параллелепипеда:

Прямоугольный параллелепипед, все грани которого являются равными квадратами, называется кубом. Помимо прочего, куб является правильной четырехугольной призмой, и вообще правильным многогранником. Для куба справедливы все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:
- Абсолютно все рёбра куба равны между собой.
- Диагональ кубаd и длина его ребра a связаны соотношением:

Из формулы для объема прямоугольного параллелепипеда можно получить следующую формулу дляобъема куба:

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Пирамида

Определения:

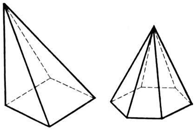
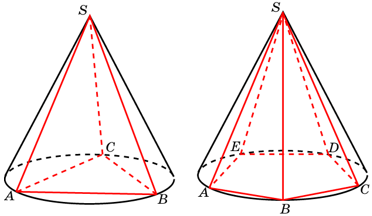
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. На рисунке приведены примеры: четырёхугольная и шестиугольная пирамиды.

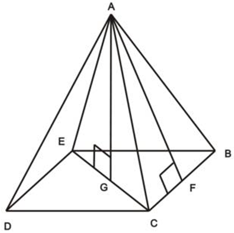
Основание – многоугольник, которому не принадлежит вершина пирамиды. На чертеже основание это BCDE.
Грани, отличные от основания, называются боковыми. На чертеже это: ABC, ACD, ADE и AEB.
Общая вершина боковых граней называется вершиной пирамиды (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины). На чертеже это A.
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. На чертеже это:AB, AC, AD и AE.
Обозначая пирамиду, сначала называют ее вершину, а затем – вершины основания. Для пирамиды с чертежа обозначение будет таким: ABCDE.

Высотойпирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H. На чертеже высота это AG. Обратите внимание:только в случае если пирамида является правильной четырехугольной пирамидой (как на чертеже) высота пирамиды попадает на диагональ основания. В остальных случаях это не так. В общем случае у произвольной пирамиды, точка пересечения высоты и основания может оказаться где угодно.
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. На чертеже это, например, AF.
Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину пирамиды и диагональ основания. На чертеже это, например, ACE.

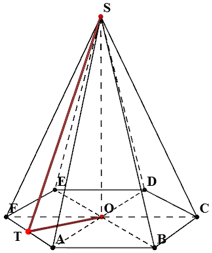
Еще один стереометрический чертеж с обозначениями для лучшего запоминания (на рисунке правильная треугольная пирамида):

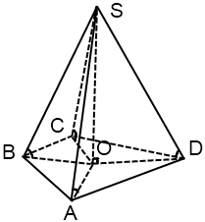
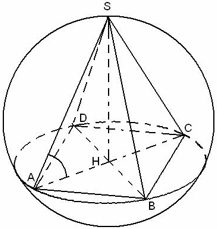
Если все боковые ребра (SA, SB, SC, SD на чертеже ниже) пирамиды равны, то:

Около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр (точка O). Иными словами, высота (отрезок SO), опущенная из вершины такой пирамиды на основание (ABCD), попадает в центр описанной вокруг основания окружности, т.е. в точку пересечения посерединных перпендикуляров основания.
Боковые ребра образуют с плоскостью основания равные углы (на чертеже ниже это углы SAO, SBO, SCO,SDO).

Важно: Также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

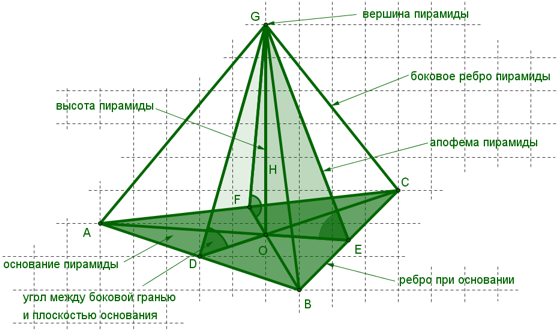
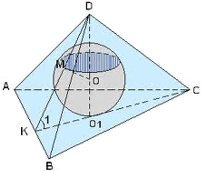
Если боковые грани наклонены к плоскости основания под одним углом (углы DMN, DKN, DLN на чертеже ниже равны), то:

В основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр (точкаN). Иными словами, высота (отрезок DN), опущенная из вершины такой пирамиды на основание, попадает в центр вписанной в основание окружности, т.е. в точку пересечения биссектрис основания.
Высоты боковых граней (апофемы) равны. На чертеже ниже DK, DL, DM – равные апофемы.
Площадь боковой поверхности такой пирамиды равна половине произведения периметра основания на высоту боковой грани (апофему).

где: P – периметр основания, a – длина апофемы.

Важно: Также верно и обратное, то есть если в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в её центр, то все боковые грани наклонены к плоскости основания под одним углом и высоты боковых граней (апофемы) равны.

Правильная пирамида

Определение: Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:

Все боковые ребра правильной пирамиды равны.
Все боковые грани правильной пирамиды наклонены к плоскости основания под одним углом.

Важное замечание: Как видим правильные пирамиды являются одними из тех пирамид к которым относятся свойства, изложенные чуть выше. Действительно, если основание правильной пирамиды – это правильный многоугольник, то центр его вписанной и описанной окружностей совпадают, а вершина правильной пирамиды проецируется именно в этот центр (по определению). Однако важно понимать, что не только правильныепирамиды могут обладать свойствами, о которых говорилось выше.

В правильной пирамиде все боковые грани – равные равнобедренные треугольники.
В любую правильную пирамиду можно как вписать сферу, так и описать около неё сферу.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Формулы для объема и площади пирамиды

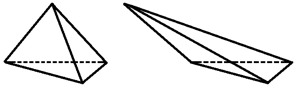
Теорема (об объеме пирамид, имеющих равные высоты и равные площади оснований). Две пирамиды, имеющие равные высоты и равные площади оснований, имеют равные объемы (Вы конечно, наверняка уже знаете формулу для объема пирамиды, ну или видите ее несколькими строчками ниже, и Вам кажется это утверждение очевидным, но на самом деле, если судить «на глаз», то данная теорема не так уж и очевидна (см. рисунок ниже). Это относится кстати и к другим многогранникам и геометрическим фигурам: их внешний вид обманчив, поэтому, действительно – в математике нужно доверять только формулам и правильным расчетам).

Объём пирамиды может быть вычислен по формуле:

где: S осн – площадь основания пирамиды, h – высота пирамиды.

Боковая поверхность пирамиды равна сумме площадей боковых граней. Для площади боковой поверхности пирамиды можно формально записать такую стереометрическую формулу:

где: S бок – площадь боковой поверхности, S 1 , S 2 , S 3 – площади боковых граней.

Полная поверхность пирамиды равна сумме площади боковой поверхности и площади основания:

Тетраэдр

Определения:

Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, иными словами, треугольная пирамида. Для тетраэдра любая из его граней может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 рёбер.
Тетраэдр называется правильным, если все его грани – равносторонние треугольники. У правильного тетраэдра:
1. Все ребра правильного тетраэдра равны между собой.
2. Все грани правильного тетраэдра равны между собой.
3. Периметры, площади, высоты и все остальные элементы всех граней соответственно равны между собой.

На чертеже изображен правильный тетраэдр, при этом треугольники ABC, ADC, CBD, BAD – равны. Из общих формул для объема и площадей пирамиды, а также знаний из планиметрии не сложно получить формулы дляобъема и площадей правильного тетраэдра (а – длина ребра):

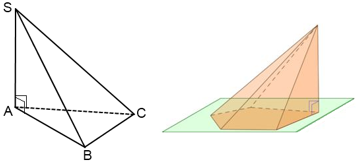
Прямоугольная пирамида

Определение: При решении задач по стереометрии, пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В таком случае, это ребро и является высотой пирамиды. Ниже примеры треугольной и пятиугольной прямоугольных пирамид. На рисунке слева SA – ребро, являющееся одновременно высотой.

Усечённая пирамида

Определения и свойства:

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Фигура, полученная на пересечении секущей плоскости и исходной пирамиды, также называетсяоснованием усеченной пирамиды. Итак, у усеченной пирамиды на чертеже два основания: ABC и A 1 B 1 C 1 .
Боковые грани усечённой пирамиды являются трапециями. На чертеже это, например, AA 1 B 1B.
Боковыми ребрами усеченной пирамиды называются части ребер исходной пирамиды, заключенные между основаниями. На чертеже это, например, AA 1 .
Высотой усеченной пирамиды называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания к плоскости другого основания.
Усеченная пирамида называется правильной, если она является многогранником, который отсекается плоскостью, параллельной основанию правильной пирамиды.
Основания правильной усеченной пирамиды – правильные многоугольники.
Боковые грани правильной усеченной пирамиды – равнобедренные трапеции.
Апофемой правильной усеченной пирамиды называется высота ее боковой грани.
Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.

Формулы для усеченной пирамиды

Объём усечённой пирамиды равен:

где: S 1 и S 2 – площади оснований, h – высота усечённой пирамиды. Однако на практике, удобнее искать объем усеченной пирамиды так: можно достроить усечённую пирамиду до пирамиды, продлив до пересечения боковые рёбра. Тогда объём усечённой пирамиды можно найти, как разность объёмов всей пирамиды и достроенной части. Площадь боковой поверхности также можно искать как разность между площадями боковой поверхности всей пирамиды и достроенной части. Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы:

где: P 1 и P 2 – периметры оснований правильной усеченной пирамиды, а – длина апофемы. Площадь полной поверхности любой усеченной пирамиды, очевидно, находится как сумма площадей оснований и боковой поверхности:

Пирамида и шар (сфера)

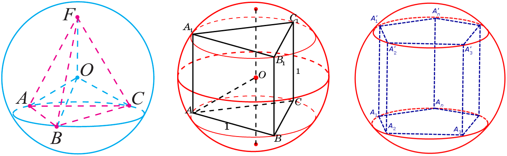
Теорема: Около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит вписанный многоугольник (т.е. многоугольник около которого можно описать сферу). Данное условие является необходимым и достаточным. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им.

Замечание: Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу. Однако, список пирамид около которых можно описать сферу не исчерпывается этими типами пирамид. На чертеже справа, на высоте SH надо выбрать точку О, равноудалённую от всех вершин пирамиды: SO = OВ = OС = OD = OA. Тогда точка О – центр описанного шара.

Теорема: В пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.

Замечание: Вы, очевидно, не поняли того, что прочитали строчкой выше. Однако, главное запомнить, что любая правильная пирамида является такой, в которую можно вписать сферу. При этом список пирамид, в которые можно вписать сферу не исчерпывается правильными.

Определение: Биссекторная плоскость делит двугранный угол пополам, а каждая точка биссекторной плоскости равноудалена от граней, образующих двугранный угол. На рисунке справа плоскость γ является биссекторной плоскостью двугранного угла, образованного плоскостями α и β.

На стереометрическом чертеже ниже изображен шар вписанный в пирамиду (или пирамида описанная около шара), при этом точка О – центр вписанного шара. Данная точка О равноудалена от всех граней шара, например:

Пирамида и конус

В стереометрии конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие).

Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие).

Важное свойство: Высоты у таких конусов и пирамид равны между собой.

Пирамида и цилиндр

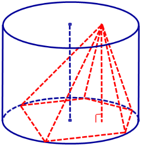
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.

Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды – вписанный многоугольник (необходимое и достаточное условие).

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Сфера и шар

Определения:

Сфера – замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.
Хордой сферы называется отрезок, соединяющий две точки сферы.
Диаметром сферы называется хорда, проходящая через ее центр. Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.
Шар – геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от некоторого центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Обратите внимание: поверхность (или граница) шара называется сферой. Можно дать и такое определение шара: шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.
Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей данного шара.
Разница между шаром и сферой аналогична разнице между кругом и окружностью. Окружность – это линия, а круг – это ещё и все точки внутри этой линии. Сфера – это оболочка, а шар – это ещё и все точки внутри этой оболочки.
Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.
Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).

Теоремы:

Теорема 1 (о сечении сферы плоскостью). Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.
Теорема 2 (о сечении шара плоскостью). Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.

Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. Aи B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.

Определения:

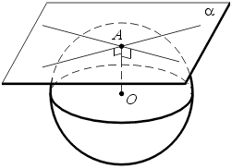
Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.
Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.
Любая прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку – точку касания.

Теоремы:

Теорема 1 (признак касательной плоскости к сфере). Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
Теорема 2 (о свойстве касательной плоскости к сфере). Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.

Многогранники и сфера

Определение: В стереометрии многогранник (например, пирамида или призма) называется вписанным в сферу, если все его вершины лежат на сфере. При этом сфера называется описанной около многогранника (пирамиды, призмы). Аналогично: многогранник называется вписанным в шар, если все его вершины лежат на границе этого шара. При этом шар называется описанным около многогранника.

Важное свойство: Центр сферы, описанной около многогранника, находится на расстоянии, равном радиусу R сферы, от каждой вершины многогранника. Приведем примеры вписанных в сферу многогранников:

Определение: Многогранник называется описанным около сферы (шара), если сфера (шар) касается всехграней многогранника. При этом сфера и шар называются вписанными в многогранник.

Важно: Центр сферы, вписанной в многогранник, находится на расстоянии, равном радиусу r сферы, от каждой из плоскостей, содержащих грани многогранника. Приведем примеры описанных около сферы многогранников:

Объем и площадь поверхности шара

Теоремы:

Теорема 1 (о площади сферы). Площадь сферы равна:

где: R – радиус сферы.

Теорема 2 (об объеме шара). Объем шара радиусом R вычисляется по формуле:

Шаровой сегмент, слой, сектор

Шаровой сегмент

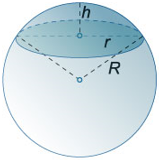
В стереометрии шаровым сегментом называется часть шара, отсекаемая секущей плоскостью. При этом соотношение между высотой, радиусом основания сегмента и радиусом шара:

где: h − высота сегмента, r − радиус основания сегмента, R − радиус шара. Площадь основания шарового сегмента:

Площадь внешней поверхности шарового сегмента:

Площадь полной поверхности шарового сегмента:

Объем шарового сегмента:

Шаровой слой

В стереометрии шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями. Площадь внешней поверхности шарового слоя:

где: h − высота шарового слоя, R − радиус шара. Площадь полной поверхности шарового слоя:

где: h − высота шарового слоя, R − радиус шара, r 1 , r 2 − радиусы оснований шарового слоя, S 1 , S 2 − площади этих оснований. Объем шарового слоя проще всего искать как разность объемов двух шаровых сегментов.

Шаровой сектор

В стереометрии шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше чем пол шара. Площадь полной поверхности шарового сектора:

где: h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара. Объем шарового сектора вычисляется по формуле:

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Цилиндр

Определения:

В некоторой плоскости рассмотрим окружность с центром O и радиусом R. Через каждую точку окружности проведем прямую, перпендикулярную плоскости окружности. Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности. Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.

Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим цилиндрической поверхности. Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.
Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями, которые перпендикулярны ее образующим, а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях, называются основаниями цилиндра. Основания цилиндра – это два равных круга.
Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра. Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.
Осью цилиндра называется отрезок, соединяющий центры кругов, являющихся основаниями цилиндра.
Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания. В цилиндре высота равна образующей.
Радиусом цилиндра называется радиус его оснований.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
Цилиндр можно получить поворотом прямоугольника вокруг одной из его сторон на 360°.
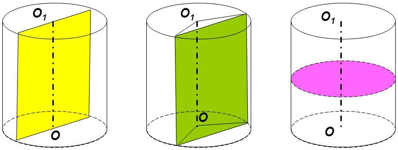
Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие, а две другие – хорды оснований цилиндра.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.
Если секущая плоскость, перпендикулярна оси цилиндра, то в сечении образуется круг равный основаниям. На чертеже ниже: слева – осевое сечение; в центре – сечение параллельное оси цилиндра; справа – сечение параллельное основанию цилиндра.

Цилиндр и призма

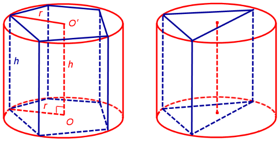
Призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра. В этом случае цилиндр называется описанным около призмы. Высота призмы и высота цилиндра в этом случае будут равны. Все боковые ребра призмы будут принадлежать боковой поверхности цилиндра и совпадать с его образующими. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать в такой цилиндр можно также только прямую призму. Примеры:

Призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра. В этом случае цилиндр называется вписанным в призму. Высота призмы и высота цилиндра в этом случае также будут равны. Все боковые ребра призмы будут параллельны образующим цилиндра. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать такой цилиндр можно только в прямую призму. Примеры:

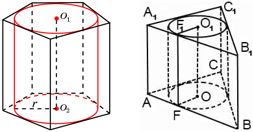
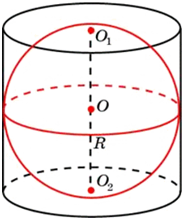
Цилиндр и сфера

Сфера (шар) называется вписанной в цилиндр, если она касается оснований цилиндра и каждой его образующей. При этом цилиндр называется описанным около сферы (шара). Сферу можно вписать в цилиндр, только если это равносторонний цилиндр, т.е. диаметр его основания и высота равны между собой. Центром вписанной сферы будет служить середина оси цилиндра, а радиус этой сферы будет совпадать с радиусом цилиндра. Пример:

Цилиндр называется вписанным в сферу, если окружности оснований цилиндра являются сечениями сферы. Цилиндр называется вписанным в шар, если основания цилиндра являются сечениями шара. При этом шар (сфера) называется описанным около цилиндра. Вокруг любого цилиндра можно описать сферу. Центром описанной сферы также будет служить середина оси цилиндра. Пример:

На основе теоремы Пифагора легко доказать следующую формулу, связывающую радиус описанной сферы (R), высоту цилиндра (h) и радиус цилиндра (r):

Объем и площадь боковой и полной поверхностей цилиндра

Теорема 1 (о площади боковой поверхности цилиндра): Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту:

где: R – радиус основания цилиндра, h – его высота. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности прямой призмы.

Площадью полной поверхности цилиндра, как обычно в стереометрии, называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра (т.е. просто площадь круга) вычисляется по формуле:

Следовательно, площадь полной поверхности цилиндра S полн. цилиндра вычисляется по формуле:

Теорема 2 (об объеме цилиндра): Объем цилиндра равен произведению площади основания на высоту:

где: R и h – радиус и высота цилиндра соответственно. Эта формула также легко выводится (доказывается) на основе формулы для объема призмы.

Теорема 3 (Архимеда): Объём шара в полтора раза меньше объёма, описанного вокруг него цилиндра, а площадь поверхности такого шара в полтора раза меньше площади полной поверхности того же цилиндра:

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Конус

Определения:

Конусом (точнее, круговым конусом) называется тело, которое состоит из круга (называемого основанием конуса), точки, не лежащей в плоскости этого круга (называемой вершиной конуса) и всех возможных отрезков, соединяющих вершину конуса с точками основания. Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.

Отрезки (или их длины), соединяющие вершину конуса с точками окружности основания, называютсяобразующими конуса. Все образующие прямого кругового конуса равны между собой.
Поверхность конуса состоит из основания конуса (круга) и боковой поверхности (составленной из всех возможных образующих).
Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом.
Наглядно прямой круговой конус можно представлять себе, как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. При этом боковая поверхность конуса образуется вращением гипотенузы, а основание – вращением катета, не являющимся осью.
Радиусом конуса называется радиус его основания.
Высотой конуса называется перпендикуляр (или его длина), опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту, т.е. прямая проходящая через центр основания и вершину.
Если секущая плоскость проходит через ось конуса, то сечение равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называетсяосевым.

Если секущая плоскость проходит через внутреннюю точку высоты конуса и перпендикулярна ей, то сечением конуса является круг, центр которого есть точка пересечения высоты и этой плоскости.
Высота (h), радиус (R) и длина образующей (l) прямого кругового конуса удовлетворяют очевидному соотношению:

Объем и площадь боковой и полной поверхностей конуса

Теорема 1 (о площади боковой поверхности конуса). Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:

где: R – радиус основания конуса, l – длина образующей конуса. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности правильной пирамиды.

Площадью полной поверхности конуса называется сумма площади боковой поверхности и площади основания. Площадь основания конуса (т.е. просто площадь круга) равна: S осн = πR 2 . Следовательно, площадь полной поверхности конуса S полн. конуса вычисляется по формуле:

Теорема 2 (об объеме конуса). Объем конуса равен одной трети произведения площади основания на высоту:

где: R – радиус основания конуса, h – его высота. Эта формула также легко выводится (доказывается) на основе формулы для объема пирамиды.

Усеченный конус

Определения:

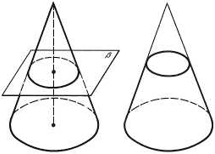
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.

Основание исходного конуса и круг, получающийся в сечении этого конуса плоскостью, называютсяоснованиями, а отрезок, соединяющий их центры — высотой усеченного конуса.
Прямая проходящая через высоту усеченного конуса (т.е. через центры его оснований) является его осью.
Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конуса, расположенные между основаниями усеченного конуса, называются его образующими.
Все образующие усеченного конуса равны между собой.
Усеченный конус может быть получен при повороте на 360° прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

Формулы для усеченного конуса:

Объем усеченного конуса равен разности объемов полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Объём усечённого конуса вычисляется по формуле:

где: S 1 = πr 1 2 и S 2 = πr 2 2 – площади оснований, h – высота усечённого конуса, r 1 и r 2 – радиусы верхнего и нижнего оснований усеченного конуса. Однако на практике, всё же удобнее искать объем усеченного конуса как разность объёмов исходного конуса и отсеченной части. Площадь боковой поверхности усеченного конуса также можно искать как разность между площадями боковой поверхности исходного конуса и отсеченной части.

Действительно, площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Площадь боковой поверхности усеченного конуса вычисляется по формуле:

где: P 1 = 2πr 1 и P 2 = 2πr 2 – периметры оснований усеченного конуса, l – длина образующей. Площадь полной поверхности усеченного конуса, очевидно, находится как сумма площадей оснований и боковой поверхности:

Обратите внимание, что формулы для объема и площади боковой поверхности усеченного конуса получены на основе формул для аналогичных характеристик правильной усеченной пирамиды.

Конус и сфера

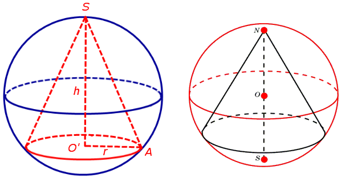
Конус называется вписанным в сферу (шар), если его вершина принадлежит сфере (границе шара), а окружность основания (само основание) является сечением сферы (шара). При этом сфера (шар) называется описанной около конуса. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описанной сферы будет лежать на прямой содержащей высоту конуса, а радиус этой сферы будет равен радиусу окружности, описанной около осевого сечения конуса (это сечение является равнобедренным треугольником). Примеры:

Сфера (шар) называется вписанной в конус, если сфера (шар) касается основания конуса и каждой его образующей. При этом конус называется описанным около сферы (шара). В прямой круговой конус всегда можно вписать сферу. Её центр будет лежать на высоте конуса, а радиус вписанной сферы будет равен радиусу окружности, вписанной в осевое сечение конуса (это сечение является равнобедренным треугольником). Примеры: