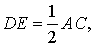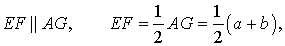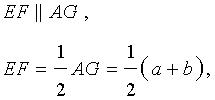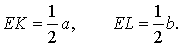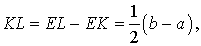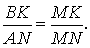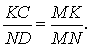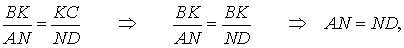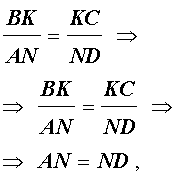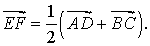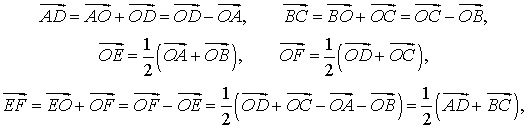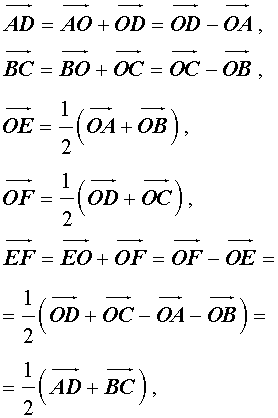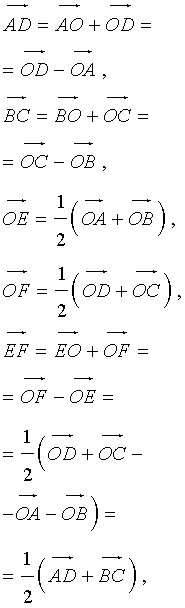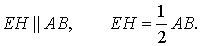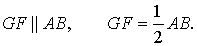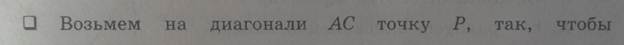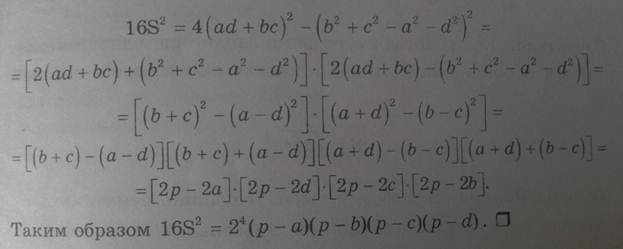В данной публикации мы рассмотрим определение и основные свойства средних линий выпуклого четырехугольника касательно точки их пересечения, соотношения с диагоналями и т.д.
Примечание: далее мы будем рассматривать только выпуклую фигуру.
- Определение средней линии четырехугольника
- Свойства средней линии четырехугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Средние линии
- Средние линии треугольника
- Средняя линия трапеции
- Средние линии четырехугольника. Теорема Вариньона
- Средние линии тетраэдра
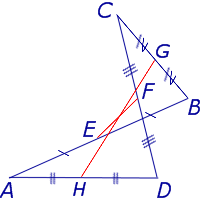
- Теорема о двух средних линиях четырехугольника и отрезке соединяющем середины его диагоналей
- 🔍 Видео
Видео:🔥Вся теория по четырёхугольникам и окружностям второй части ЕГЭ за 1,5 часа🔥Скачать

Определение средней линии четырехугольника
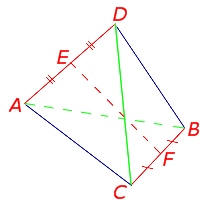
Отрезок, соединяющий середины противоположных сторон четырехугольника (т.е. не пересекающий их), называется его средней линией.
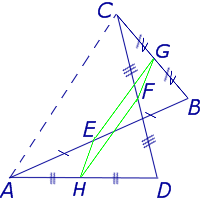
- EF – средняя линия, соединяющая середины AB и CD; AE=EB, CF=FD.
- GH – средняя линия, сеодиняющая середины BC и AD; BG=GC, AH=HD.
Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Свойства средней линии четырехугольника
Свойство 1
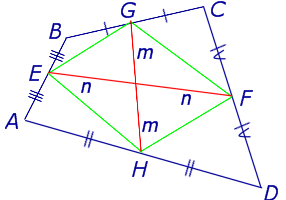
Средние линии четырехугольника пересекаются и в точке пересечения делятся пополам.
Примечание: Точка O является центроидом (или барицентром) четырехугольника.
Свойство 2
Точка пересечения средних линий четырехугольника является серединой отрезка, соединяющего середины его диагоналей.
Свойство 3
Середины сторон четырехугольника являются вершинами параллелограмма, который называется параллелограммом Вариньона.
Центром образованного таким образом параллелограмма и точкой пересечения его диагоналей является середина средних линий исходного четырехугольника, т.е. точка их пересечения – O.
Примечание: Площадь параллелограмма равняется половине площади четырехугольника.
Свойство 4
Если углы между диагоналями четырехугольника и его средней линией равны, значит диагонали имеют одинаковую длину.
Свойство 5
Средняя линия четырехугольника меньше или равна полусумме непересекающих ее сторон (при условии, что данные стороны параллельны).
EF – средняя линия, не пересекающаяся со сторонами AD и BC.
Иначе говоря, средняя линия четырехугольника равняется половине суммы не пересекающих ее сторон тогда и только тогда, когда данный четырехугольник является трапецией. В этом случае рассматриваемые стороны являются основаниями фигуры.
Свойство 6
Для вектора средней линии произвольного четырехугольника выполняется следующее равенство:
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Средние линии
 Средние линии треугольника Средние линии треугольника |
 Средняя линия трапеции Средняя линия трапеции |
 Средние линии четырехугольников. Теорема Вариньона Средние линии четырехугольников. Теорема Вариньона |
 Средние линии тетраэдра Средние линии тетраэдра |
Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Средние линии треугольника
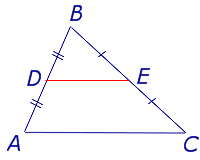
Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).
На рисунке 1 средней линией является отрезок DE .
Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
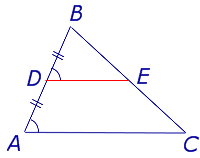
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.
Первую часть утверждения 1 мы доказали.
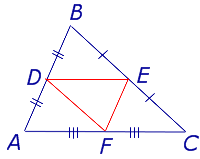
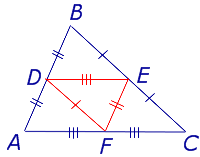
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).
Но поскольку AF = FC , то отсюда вытекает равенство
что и требуется доказать.
Доказательство утверждения 1 закончено.
- Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
- Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .
Видео:Сможешь найти расстояние между серединами диагоналей трапеции? Классика ЕГЭСкачать

Средняя линия трапеции
Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.
Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.
Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.
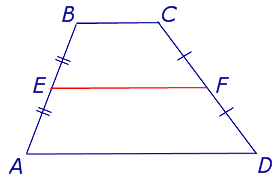
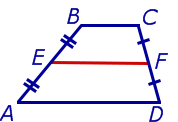
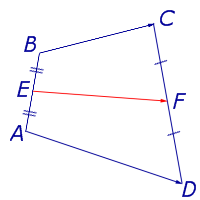
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).
На рисунке 5 средней линией трапеции является отрезок EF .
Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.
Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
что и требовалось доказать.
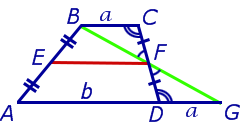
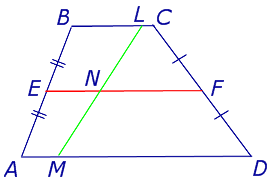
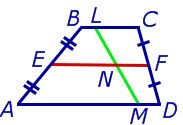
Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.
Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.
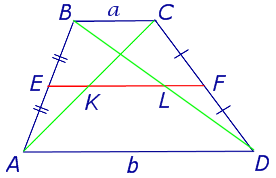
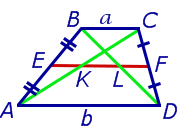
Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.
Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:
что и требовалось доказать.
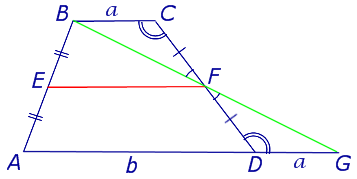
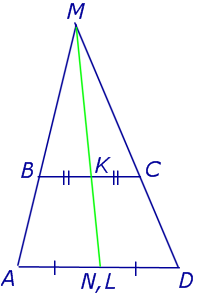
Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
Из этих соотношений получаем:
откуда вытекает, что точки N и L совпадают. Доказательство завершено.
Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.
Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.
Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
Видео:Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

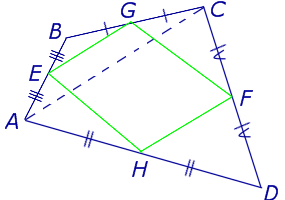
Средние линии четырехугольника. Теорема Вариньона
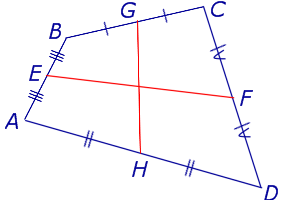
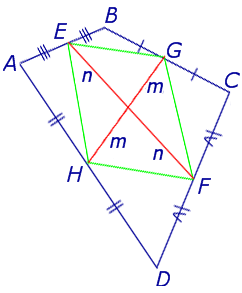
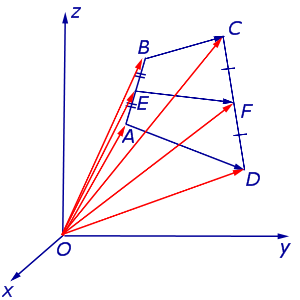
Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).
На рисунке 10 средние линии – это отрезки EF и GH .
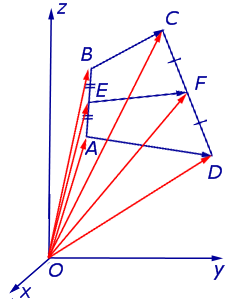
Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.
На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .
Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.
Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.
Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .
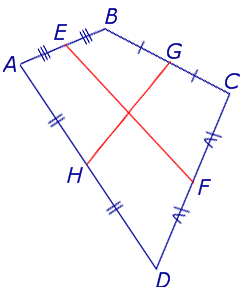
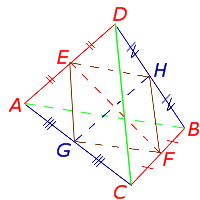
Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).
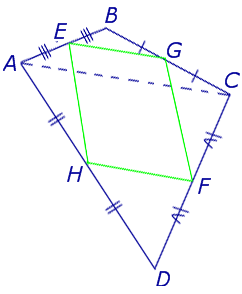
Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).
Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:
что и требовалось доказать.
Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.
Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.
Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

Средние линии тетраэдра
Тетраэдром называют произвольную треугольную пирамиду (рис.17).
У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .
Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.
У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.
Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.
Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).
Заметим, что отрезок EH является средней линией треугольника ADB , поэтому
Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .
Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:
Видео:Теорема о средней линии треугольникаСкачать

Теорема о двух средних линиях четырехугольника и отрезке соединяющем середины его диагоналей
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла. Четырехугольник, у которого угол больше развернутого называется невыпуклым
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
- Сумма углов четырёхугольника равна 2 π = 360°.
- Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
- Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
- Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Теорема Вариньона
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство
Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников 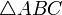
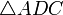
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ 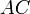
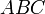
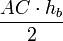
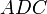
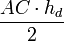
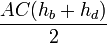
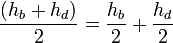
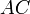
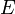
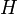
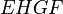
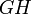
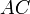
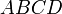
Теорема Эйлера
в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями
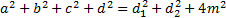

Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон
Теорема Птолемея
Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)
Если a, b, c, d – длины сторон четырёхугольника, 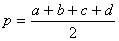
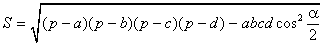
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: 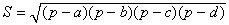
это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: 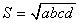
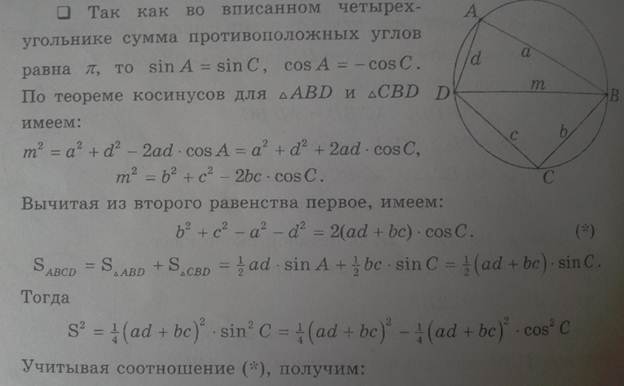
🔍 Видео
Средняя линия треугольника | Задачи 11-20 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Теорема о средней линии трапецииСкачать

Геометрия 8 класс (Урок№16 - Средняя линия треугольников и трапеции.)Скачать

Геометрия 8. Урок 7 - Средняя линия треугольника и трапецииСкачать

8 класс, 49 урок, Средняя линия трапецииСкачать

№101. Докажите, что отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаютсяСкачать

Средняя линия треугольника – 8 класс геометрияСкачать

Средняя линия треугольника | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Геометрия Докажите, что Средняя линия треугольника, соединяющая середины двух его сторонСкачать

СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА . §7 геометрия 8 классСкачать

Средняя линия треугольникаСкачать

Средняя линия треугольника. Видеоурок 13. Геометрия 8 класс.Скачать