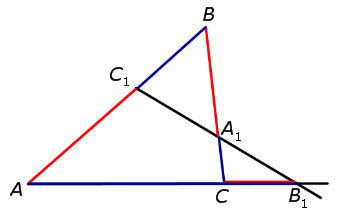
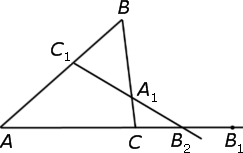
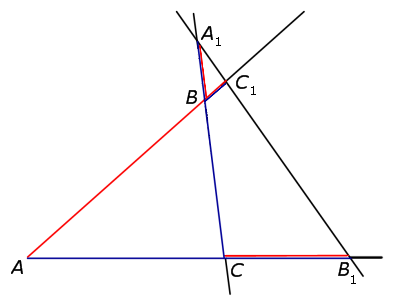
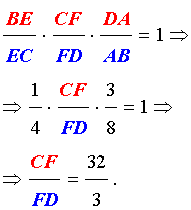
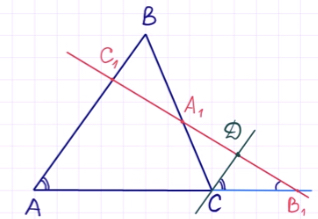
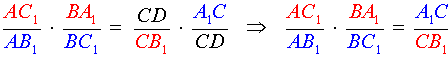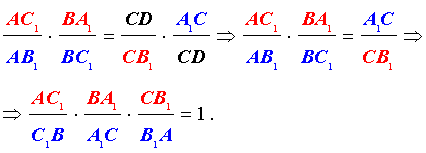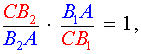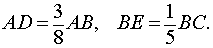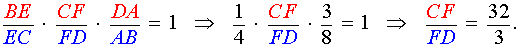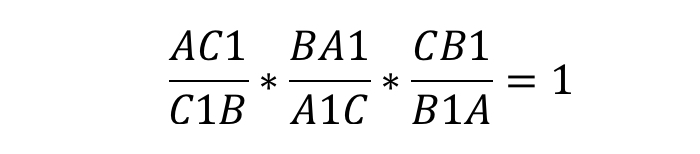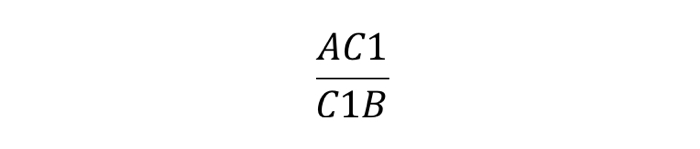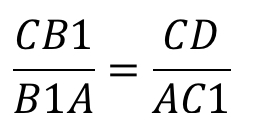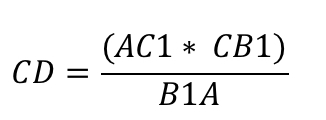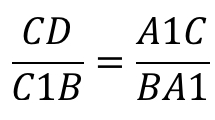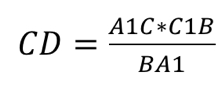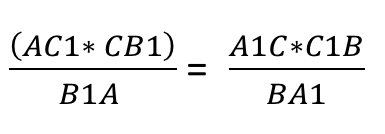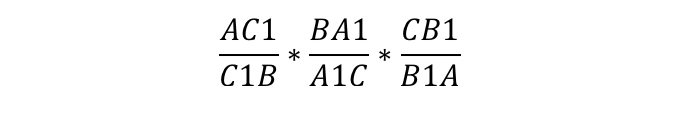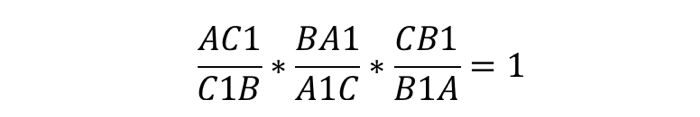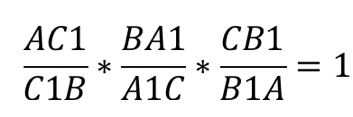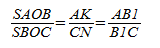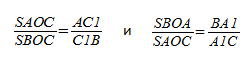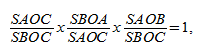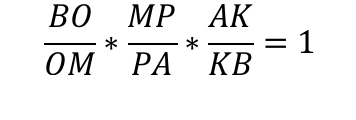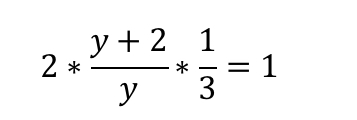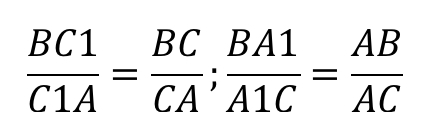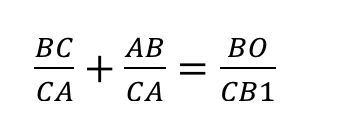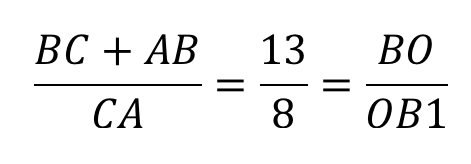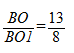Теорема Менелая 1 . Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1 , а точка B1 взята на продолжении стороны AC за точку C (рис.1), то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство
 . . | (1) |
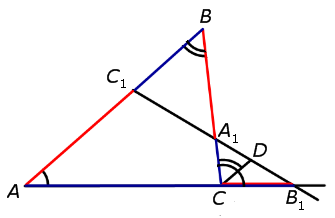
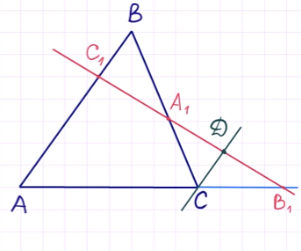
Доказательство необходимости . Докажем, что если точки C1, A1 и B1 лежат на одной прямой, то выполнено равенство (1). Для этого проведём через точку C прямую, параллельную прямой AB , и обозначим буквой D её точку пересечения с прямой C1B1 (рис.2).
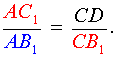 | (2) |
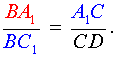 | (3) |
Перемножая равенства (2) и (3), получим
Доказательство необходимости завершено.
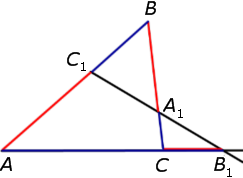
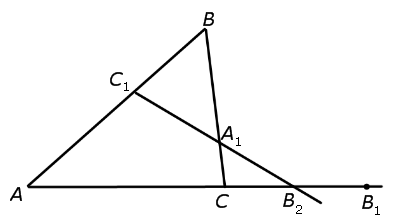
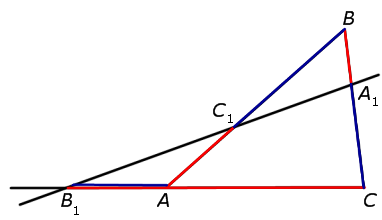
Доказательство достаточности . Докажем, что если выполнено равенство (1), то точки C1, A1 и B1 лежат на одной прямой. Воспользуемся методом «от противного». С этой целью проведём прямую через точки C1 и A1 и обозначим символом B2 точку пересечения этой прямой с прямой AC (рис. 3).
Поскольку точки C1, A1 и B2 лежат на одной прямой, то выполнено равенство
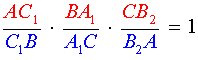 . . | (4) |
Кроме того, выполнено равенство
 . . | (1) |
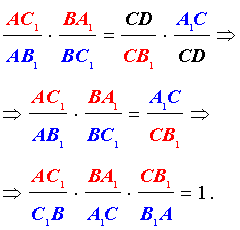
Разделив равенство (4) на равенство (1), получим равенство
следствием которого является равенство
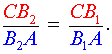 | (5) |
Доказательство достаточности завершено.
Теорема Менелая 1 доказана.
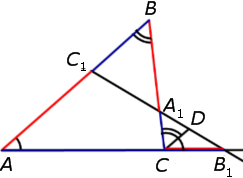
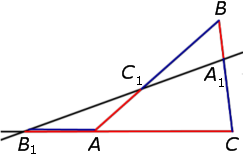
Замечание . Если чуть-чуть изменить формулировку теоремы Менелая 1, выбрав точку B1 на продолжении стороны AC за точку A (рис.4), то доказательство теоремы Менелая практически не изменится, и мы предоставляем его читателю в качестве упражнения.
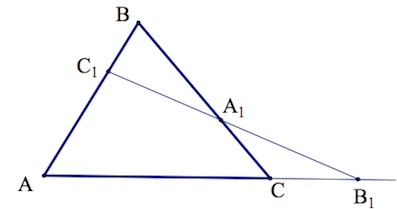
Теорема Менелая 2 . Если на продолжениях сторон AB , BC и AC треугольника ABC взяты соответственно точки C1, A1 и B1 (рис.5), то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство
 . . | (6) |
Замечание . Доказательство теоремы Менелая 2 почти дословно повторяет доказательство теоремы Менелая 1, и мы оставляем его читателю в качестве упражнения.
Для того, чтобы показать, как можно применять теорему Менелая , решим следующую задачу.
Задача . На сторонах AB и BC треугольника ABC взяты точки D и E соответственно, причем
Отрезки AE и CD пересекаются в точке F (рис.6). В каком отношении отрезки AE и CD делятся точкой F ?
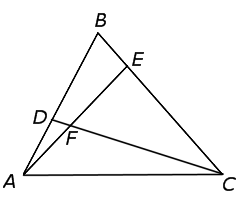
Решение . Применив к треугольнику BCD теорему Менелая (рис. 7),
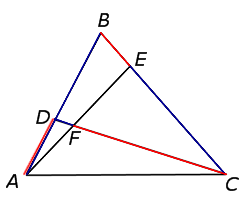
Применив к треугольнику ABE теорему Менелая (рис. 8),
- Теорема Менелая
- Определение Теоремы Менелая
- Доказательство теоремы Менелая
- Теорема Менелая пример (задача с решением)
- Что такое теорема Чевы?
- Теорема Чевы и Менелая — формулировка, применение и примеры решения
- Формулировка теоремы Менелая
- Доказательство теоремы
- Формулировка теоремы Чевы
- Доказательство теоремы
- Применение теорем Чевы и Менелая при решении задач ЕГЭ
- Задача 1
- Задача 2
- 🔍 Видео
Видео:Теорема Менелая | Математика | TutorOnlineСкачать

Теорема Менелая
Видео:Теорема Менелая | Осторожно, спойлер! | Борис Трушин !Скачать

Определение Теоремы Менелая
Теорема Менелая показывает соотношение сторон треугольника, которое получается, когда прямая пересекает две стороны треугольника и продолжение третьей.
С помощью этой теоремы можно получить соотношения сторон треугольника и доказать коллинеарность точек, которые находятся на данном треугольнике (на двух сторонах и продолжении третьей).
Коллинеарными точками называются три или более точки, которые лежат на одной прямой.
Теорема Менелая гласит:
BD/DC * CE/EA * AF/FB = 1
Шаг 1. Есть треугольник ABC. Прямая пересекает две стороны треугольника, таким образом, что она не проходит через вершину треугольника (на нашем рисунке это розовая линия). Таким образом получились две точки пересечения прямой с двумя сторонами треугольника (точки E и D). Третью сторону (AB) нужно продолжить до пересечения (получилась точка пересечения F).
Шаг 2. Берём точку треугольника и начинаем двигаться в другую точку треугольника, проходя через точку пересечения (потом делим один на другой): BD/DC
Обратите внимание, что в такой записи видно точку пересечения посередине («DD»), а B и C (сторона треугольника, по которой мы идём) по бокам. Т. е. мы идём из B к C через D. Можно написать точки стороны, по которой мы идём («BC»), оставив небольшое место между ними, и потом вставить между ними дважды точку пересечения со знаком дроби («D/D»).
В записи дробью точка, через которую мы идём повторяется наискосок.
На рисунке обозначить карандашом стрелочками по какой стороне мы уже прошлись и в какую сторону, и не запутаетесь.
Шаг 3. Идём дальше по треугольнику, делаем сторону CA — это будто прийти от C к A через E, что получается CE/EA.
Эти две стороны умножаются и в тетради, записывается всё вместе:
Шаг 4. Теперь делаем сторону AB через точку F — из A мы сначала пойдём в F, а потом уже вернёмся к B, получится так: AF/FB.
Шаг 5. Перемножаем всё вместе:
BD/DC * CE/EA * AF/FB
Теорема Менелая гласит:
BD/DC * CE/EA * AF/FB = 1
Видео:Теорема Менелая. Убийца ГРОБА на ЕГЭ 2020 по профильной математикеСкачать

Доказательство теоремы Менелая
Есть много способов доказать эту теорему, этот называется «Доказательство с подобными треугольниками»:
Проводим линию, которая параллельна QN через точку A, чтобы пересечь сторону BC в точке M.
Видео:Теорема МенелаяСкачать

Теорема Менелая пример (задача с решением)
Есть треугольник АВС. На стороне ВС стоит точка L, такая, что LC = 3BL. За точку А идёт продолжение стороны АС, где взята точка М, таким образом, что МА = АС. Прямая ML пересекает АВ в точке F.
Найдите соотношение BF/FA:
1. Мы знаем, что МА = АС, LC = 3BL.
2. Прямая ML пересекает две стороны треугольника АВС и является продолжением третьей, значит по теореме Менелая:
Видео:Вебинар 4. Планиметрия. Теоремы Менелая и Чевы в действииСкачать

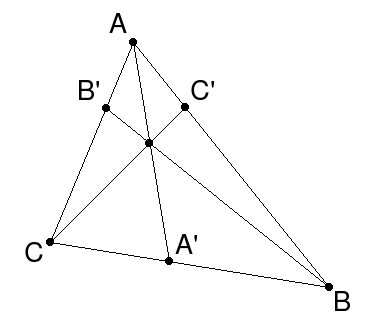
Что такое теорема Чевы?
Пусть на сторонах треугольника ABC отмечены точки A’, B’ и C’. Отрезки AA’, BB’ и CC’ пересекаются в одной точке тогда и только тогда, когда справедливо равенство:
Заметьте, что логика та же самая: идём из А в С через В’ и т. д.
Чевиана — это отрезок, который соединяет вершину треугольника с точкой на противоположной стороне.
Видео:#224. Теоремы Менелая, Чевы, Ван-Обеля. Точки Жергонна и НагеляСкачать

Теорема Чевы и Менелая — формулировка, применение и примеры решения
Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания.
Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.
Именно для этого мы подготовили данный материал. В нем вы узнаете, чем интересны данные основы, принципы их доказательств и рассмотрите решения некоторых задач из ЕГЭ.
Видео:✓ Теорема Чевы | Осторожно, спойлер! | Борис ТрушинСкачать

Формулировка теоремы Менелая
Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.
Прежде чем приступить к проработке, сделаем соответствующий рисунок.
Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.
Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.
Если мы видим приведённый выше рисунок, можно записать формулу:
Запомнить отношение просто: действуем по принципу «вершина — точка, точка — вершина». То есть, если на стороне AB нам дана некоторая точка C1, их отношенное записывается следующим образом:
Доказательство теоремы
Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:
Обозначим точку пересечения данной прямой с B1C1 через точку D.
В таком случае мы получим несколько пар подобных треугольников.
Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B1CD и B1AC1. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B1 между ними.
Углы B1CD и B1AC1 равны как соответственные при параллельных прямых CD, AB и секущей AC.
Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:
Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.
Используя описанное равенства, применив свойства пропорции, запишем:
Запишем следующую пару подобных треугольников: треугольники CDA1 и BC1A1 подобны, так как углы CA1D и BA1C1 равны как вертикальные. Кроме этого, угол CDA1 равен углу BC1A1, как накрест лежащие при параллельных прямых CD, AB и секущей C1D.
Покажем это на рисунке:
Из данного подобия можно записать некоторую пропорциональность сходственных сторон:
Так же выразим CD:
Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.
Таким образом получаем:
Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:
Что и требовалось доказать.
Видео:ТЕОРЕМА МЕНЕЛАЯ ЧАСТЬ I shorts #егэ #огэ #математика #теоремаСкачать

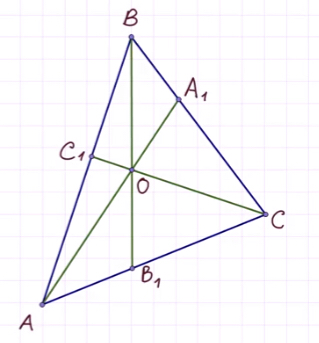
Формулировка теоремы Чевы
Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.
Рассматриваемая теорема была доказана ученым в 1678 г.
Рассмотрим приведённый ниже рисунок:
Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:
В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами».
Доказательство теоремы
Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.
Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:
Обозначим за O точку пересечения данных прямых.
Продлим медиану BB1.
Проведём перпендикуляры из вершин A и С таким образом:
Треугольники AKB1 и CNB1 подобны по острому углу.
Теперь перемножим равенства:
что и требовалось доказать.
Видео:Геометрия: теоремы Менелая, Чевы | Профильная математика ЕГЭ 2023 | УмскулСкачать

Применение теорем Чевы и Менелая при решении задач ЕГЭ
Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.
Задача 1
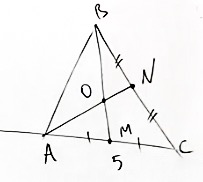
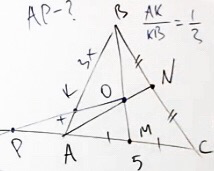
Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.
Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.
AC = 4 см, AM = 2 см.
Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.
Сторону AP обозначим за y.
Найти: чему равен отрезок AP.
Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.
Рассмотрим треугольник ABM. Для него берём прямую OP.
Таким образом мы нашли искомые точки P, A, M, O, K и B.
Запишем теорему Менелая к данному рисунку.
Подставляем в это соотношение известные данные:
В итоге мы получаем, что y = 4.
Ответ: отрезок AP = 4 см.
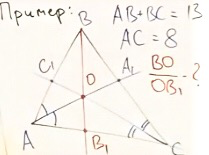
Задача 2
Задача, связанная со свойствами теоремы Чевы.
сумма AB и BC равна 13;
Найти: отношение BO и OB1.
Итак, запишем отношение:
Конечным результатом является дробь 13/8.
🔍 Видео
11 класс, 50 урок, Теорема МенелаяСкачать

Вебинар 3. Лемма о трезубце. Теорема Менелая, Чевы, Ван - Обеля. Свойства ортоцентра.Скачать

Теорема МенелаяСкачать

РАЗБИРАЕМ ТЕОРЕМУ МЕНЕЛАЯ ЧАСТЬ II ЧАСТЬ II #shorts #егэ #огэ #математика #профильныйегэСкачать

ЕГЭ геометрия Теорема Чевы Теорема МенелаяСкачать

9 класс. Геометрия. Теорема Менелая.Скачать

Теорема МенелаяСкачать

ЕГЭ задание 16 Теорема Менелая. Свойство биссектрисы треугольникаСкачать

Менелай и Чева, как запомнить за 30 секунд. Волшебная скороговоркаСкачать

Теорема Менелая (с доказательством) за 3 МИНУТЫСкачать

Теорема - убийца. 16 задача из ЕГЭ, теорема МенелаяСкачать