Расстояния от центра вписанной в прямоугольную трапецию окружности

Геометрия | 5 — 9 классы

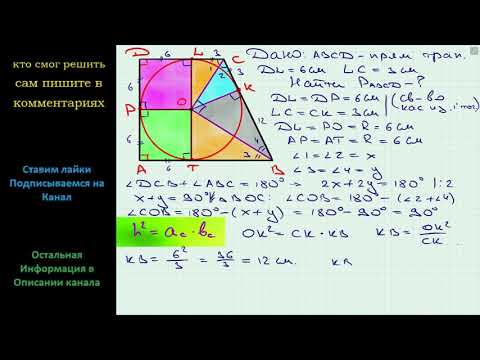
Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны, равны 6 и 8.

Найти площадь трапеции.

В трапеции АВСD.

AD⊥AB⊥BC ; О — центр вписанной окружности.

Найти площадь трапеции.

Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы его противоположных сторон равны.

Центр вписанной в углы ВСD и СDA окружности лежит на пересечении их биссектрис.

Пифагора CD = √(CO² + OD²) = 10

Радиус ОН, проведенный в точку касания окружности и боковой стороны — высота ∆ СОD.

ОН = СО•OD : CD = 6•8 : 10 = 4, 8

AD + BC = 9, 6 + 10 = 19, 6

S = H•(AD + BC) : 2 = 94, 08 (ед.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

В прямоугольно трапеции один из углов равен 60 градусам, а большая боковая сторона равна 8 см?

В прямоугольно трапеции один из углов равен 60 градусам, а большая боковая сторона равна 8 см.

Найти основание трапеции и радиус вписанной в нее окружности.

Видео:Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

Расстояния от центра вписанной в равнобедренную трапецию окружности до концов боковой стороны равны 9 и 12 см?

Расстояния от центра вписанной в равнобедренную трапецию окружности до концов боковой стороны равны 9 и 12 см.

Найдите площадь трапеции.

Видео:Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать

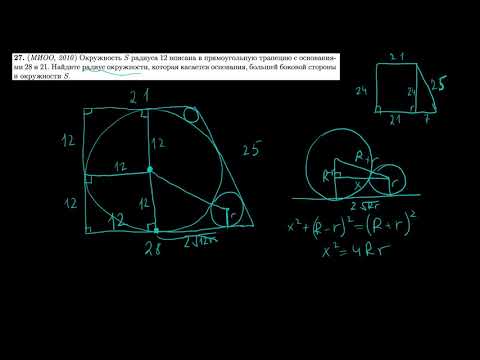
Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований 1)Доказать, что расстояние между центрами окружностей равно большей боковой стороне ?

Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований 1)Доказать, что расстояние между центрами окружностей равно большей боковой стороне трапеции 2)Найти расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной делит ее на отрезки , равные 2 и 50.

Распишите пожалуйста подробно!

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В прямоугольную трапецию вписана окружность?

В прямоугольную трапецию вписана окружность.

Точки соприкосновения делит большую боковую сторону на отрезки 4 см и 25 см.

Найти площадь трапеции.

Видео:Задача про трапецию, описанную около окружностиСкачать

Помогите пожалуйстаВ прямоугольную трапецию вписана окружность?

В прямоугольную трапецию вписана окружность.

Большая боковая сторона точкой касания делится на отрезки 9см и 16см.

Найти площадь трапеции.

Видео:Трапеция и вписанная окружностьСкачать

Вычислитm площадь прямоугольной трапеции, меньшее основание которой равно 21, а центр вписанной окружности удален от большей боковой стороны на 12 см?

Вычислитm площадь прямоугольной трапеции, меньшее основание которой равно 21, а центр вписанной окружности удален от большей боковой стороны на 12 см.

Видео:Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать

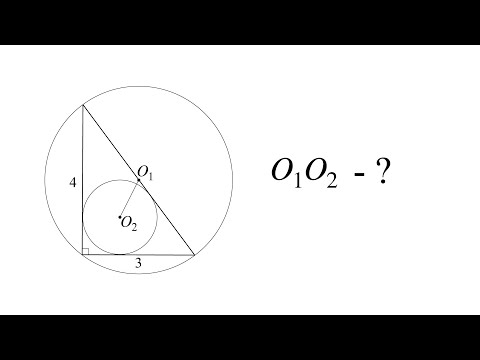
В трапеции расстояние от центра вписанной окружности до концов боковой стороны равны 156 и 65 см, а до концов большего основания 156 ; 100 см?

В трапеции расстояние от центра вписанной окружности до концов боковой стороны равны 156 и 65 см, а до концов большего основания 156 ; 100 см.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

В прямоугольную трапецию большая боковая сторона которой равна 11, вписана окружность радиусом 4?

В прямоугольную трапецию большая боковая сторона которой равна 11, вписана окружность радиусом 4.

Найдите периметр этой трапеции.

Видео:Окружность, вписанная в трапециюСкачать

Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большой боковой стороны равны 6 см и 8 см?

Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большой боковой стороны равны 6 см и 8 см.

Найдите площадь трапеции.

Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее большее основаниеСкачать

№1. в прямоугольном треугольнике один из углов равен 30 градусов радиус вписанной в неё окружности 5 см?

№1. в прямоугольном треугольнике один из углов равен 30 градусов радиус вписанной в неё окружности 5 см.

Найдите площадь треугольника.

№2. расстояние от центра вписанной в прямоугольную трапецию окружности до концов больше боковой стороны равны 6 и 8 см.

Найдите площадь трапеции.

С РИСУНКАМИ ПОЖАЛУЙСТА!

На этой странице находится вопрос Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны, равны 6 и 8?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

1) т. К. Если две стороны и угол между ними в одном треугольнике соответственно равны двум сторонам и углу между ними в другом треугольнике то такие треугольники равны ( крч посмотри теорему и спиши от туда этот признак и подставь знаки).

Обозначим вΔАВС углы х = ∠А, у = ∠В. Выразим другие углы через х и у. Т. к. ∠А и∠В — острые углы прямоугольногоΔАВС, то∠А + ∠В = 90°, поэтому х = 90° — у. Аналогично, ∠НСВ и∠В — острые углы прямоугольногоΔНВС, тогда ∠НСВ + ∠В = 90°, поэтому ∠НСВ ..

∠BCE = ∠C — ∠ECA = 90 — ∠HCA / 2 ∠CEB = 90 — ∠HCE = 90 — ∠HCA / 2 (сумма острых углов прям. Треуг. Равна 90) ∠BCE = ∠CEB = > △EBC равнобедренный, CB = BE.

1. 1 и 2 2. 1 , 2 и 3 По идее итак.

Ответ на первое : 1, 2. Ответ на второе : 1, 2, 3.

Решение на фотографии.

16 * 10 = 160 — вёдер воды.

5. а. Остальное в учебнике в параграфе.

По теореме косинусов : АС² = АВ² + ВС² — 2·АВ·ВС·cos∠ABC 14² = 8² + 10² — 2·8·10·cos∠ABC 169 = 64 + 100 — 160·cos∠ABC 160·cos∠ABC = 164 — 169 160·cos∠ABC = — 5 cos∠ABC = — 5 / 160 = — 1 / 32.

Вертикальный с этим углом будет равен 94 градусам тоже, а смежные с ними углы будут равны 180 градусов — 94 градусов = 86 градусовОтвет : 94 градуса ; 86 градусов ; 86 градусов.

Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны,равны 6 и 8. Найти площадь

Рассмотрим трапецию ABCD

AD и BC — основание

О — центр вписанной окружности

Рассмотрим треугольник COD

По теореме Пифагора
ОС=9, ОD=12, СD=15 r = ОР- высота на СD r= ОР = ОС* ОD/СD = 9*12/15 = 7,2 h = 2r = 14.4 — высота пирамиды S=(ВС+АD) * h/2 = (АВ+СD) *h/2 = (15+15) *14,4/2 = 216 Ответ: 216 №2 Пускай ABCD — заданная прямоугольная трапеция ABAD OC = 6, OD = 8 CD = 10 (по теореме Пифагора) из формулы площади треугольника можно получить равенство ON*CD = OC*OD, откуда ON = 4,8, кстати, это — радиус окружности r по свойству проекций катетов на гипотенузу найдем CN = 3,6, DN = 3,6 По свойству касательных проведенных к окружности из одной точки: CL = CN = 3,6 DK = DN = 6,4 AK = AM = OK = r = OL = BL = BM = 3,6, так как радиусы, проведенные к основаниям и перпендикулярной боковой стороне образую два равных квадрата AMOK и BMOL. Следовательно,
AB = AM + BM = 2r = 9,6,
BC = BL + CL = 4,8 + 3,6 =8,4,
AD = AK + DK = 4,8 + 6,4 =11,2.
AB — высота трапиции, по формуле площади получим:
S = AB*(AD + BC)/2 = 9,6*(8,4 + 11,2)/2 = 94,08 Ответ: 94,08

Видео:Задание 26_Прямоугольная трапеция, окружность, подобие треугольниковСкачать

Расстояния от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны равны 6 см и 8 см. Найдите площадь трапеции.

Видео:ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать

Ваш ответ

Видео:ОГЭ ЗАДАНИЕ 16 РАДИУС ОКРУЖНОСТИ ВПИСАННОЙ В ТРАПЕЦИЮ РАВЕН 18. НАЙДИТЕ ВЫСОТУ ЭТОЙ ТРАПЕЦИИСкачать

решение вопроса

Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,006
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🎬 Видео

Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать

✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Задание 26 Равнобедренная трапеция Окружности, вписанные в треугольникиСкачать

Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее меньшее основаниеСкачать