Теорема гаусса для поля в вакууме в дифференциальной форме для вектора (2 видео)

Вектор D (электрическое смещение). Теорема Гаусса для вектора b

Напряженность электростатического поля зависит от свойств среды (от с). Кроме того, вектор напряженности Е на границе диэлектриков претерпевает скачкообразное изменение. Введем для описания электрического поля системы зарядов с учетом поляризационных свойств диэлектриков вспомогательный вектор, использование которого во многих случаях упрощает изучение поля в диэлектриках.

Внутри диэлектрика поле определяется и сторонними, и связанными зарядами. Поэтому, исходя из теоремы Гаусса для вектора напряженности в вакууме (12.11) и учитывая величину плотности нескомпенсированного связанного заряда р’ в диэлектрике, запишем:

По теореме Гаусса для вектора поляризации (13.5)

Тогда имеем, что

где вектором электрического смещения (электрической индукции) называется вектор

Для изотропного диэлектрика с учетом формулы (13.3) получаем

Единица вектора электрического смещения в СИ — кулон на метр в квадрате (Кл/м 2 ).

Вектор D описывает электростатическое поле, создаваемое сторонними зарядами в вакууме, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.

Аналогично линиям напряженности можно ввести линии электрического смещения. Направление и густота линий вектора электрического смещения определяются так же, как и для вектора напряженности Е.

Согласно уравнению (13.11), теорема Гаусса в дифференциальной форме для вектора D имеет вид

т.е. дивергенция поля вектора D равна объемной плотности стороннего заряда в той же точке.

Содержание

Теорема Гаусса в дифференциальной форме
Теорема Гаусса в присутствии диэлектриков
Теорема Остроградского-Гаусса
Теорема Остроградского-Гаусса в дифференциальной форме
Теорема Остроградского-Гаусса для диэлектриков
🔥 Видео

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Теорема Гаусса в дифференциальной форме

Теорема Гаусса для вектора напряженности электростатического поля/;’ может быть сформулирована не только в интегральной форме, но и в дифференциальной (локальной) форме, отражающей локальные свойства электростатического поля. В соответствии с математической теоремой Остроградского — Гаусса поверхностный интеграл можно свести к объемному:

где объемный интеграл берется по объему V внутри замкнутой поверхности, дивергенция вычисляется по формуле

С учетом того что заряд можно также определить через объемный инте- трал но объему V, теорема Гаусса сводится к уравнению jdiv/: dV = — JpcIV,

Поскольку объем интегрирования выбран произвольно, то подынтегральное выражение должно тождественно обращаться в ноль. Таким образом, с помощью математической теоремы Остроградского — Гаусса получаем физическую теорему Гаусса для электрического поля в дифференциальной форме:

Полученная формула иллюстрирует математический смысл дивергенции как отношения потока вектора через поверхность к бесконечно малому объему.

Видео:Билет №02 "Теорема Гаусса"Скачать

Теорема Гаусса в присутствии диэлектриков

Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Теорема Остроградского-Гауса для тел в вакууме электростатического поля может быть трансформирована с помощью добавления к свободным зарядам поляризационных для получения теоремы с диэлектриками. В этом случае она запишется как:

Со значением q j s υ в качестве связанных зарядов, q i — свободных зарядов, Φ E — потока вектора напряженности электрического поля.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Теорема Остроградского-Гаусса

Если использовать вектор электрического смещения D → , то это заметно облегчает анализ поля при наличии диэлектрика. Теорему Остроградского-Гаусса при наличии диэлектрика можно записать в интегральном виде:

∮ S D → · d S → = ∑ i = 1 N q i = Q , где Q является суммарным свободным зарядом, находящийся внутри объема, который ограничен поверхностью S .

Поток вектора D → через замкнутую поверхность может быть определен только с помощью свободных зарядов. В вакууме векторы D → и E → совпадающие.

Дифференциальная форма теоремы Гаусса выражения ∮ S D → · d S → = ∑ i = 1 N q i = Q изображается как:

d i v D → = ρ с ρ , являющейся объемной плотностью свободных зарядов.

Теорема Остроградского-Гаусса вида ∮ S D → · d S → = ∑ i = 1 N q i = Q и d i v D → = ρ справедлива только в электростатике и выполняется для переменных полей. Ее относят к составной части системы уравнений Максвелла.

Видео:Урок 223. Теорема ГауссаСкачать

Теорема Остроградского-Гаусса в дифференциальной форме

Напомним формулу вектора электрической индукции:

D → = ε 0 E → + P → со значением ε 0 в качестве электрической постоянной, E → — вектора напряженности, P → — вектора поляризации.

Произведем подстановку формулы D → = ε 0 E → + P → в d i v D → = ρ :

d i v D → = d i v ε 0 E → + P → = ε 0 d i v E → + d i v P → .

При использовании теоремы Остроградского-Гаусса дифференциального вида, получим:

d i v E → = 1 ε 0 ρ — d i v P → .

Для вектора напряженности вышеуказанная формула примет вид в присутствии диэлектрика:

d i v E → = 1 ε 0 ρ + ρ s v с ρ s v , являющейся плотностью заряда. В этом случае необходимо применить d i v E → = 1 ε 0 ρ + ρ s v и d i v E → = 1 ε 0 ρ — d i v P → :

d i v P → = — 1 ε 0 c s v .

Видео:43. Применение теоремы ГауссаСкачать

Теорема Остроградского-Гаусса для диэлектриков

Теорема Остроградского-Гаусса для вектора электрического смещения в диэлектрике выглядит также, как и для напряженности поля в вакууме. Отсюда следует, что математические соотношения, получившиеся для E → поля в вакууме, аналогичны записям для однородного диэлектрика при замене напряженности электрического поля на вектор D → .

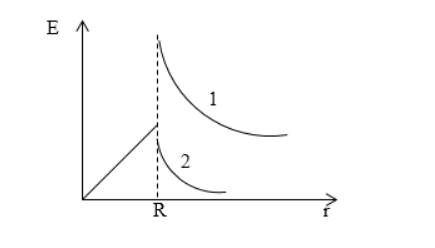
Дан диэлектрический шар, имеющий диэлектрическую проницаемость ε 1 , равномерно заряжен по объему с постоянной плотностью заряда ρ . Его нахождение в среде обусловлено наличием диэлектрической проницаемости ε 2 . Изобразить график напряженности поля шара от расстояния до его центра.

Решение

Поле, создаваемое шаром по заданным условиям, имеет сферическую симметрию. Необходимо рассмотреть его внутри шара r ≤ R . Для нахождения E ( r ) выбирается сферическая поверхность с радиусом меньше сферы. По теореме Остроградского-Гаусса:

E · S = q ε 1 ε 0 , где S — площадь поверхности сферы, которая была выделена. Отсюда следует:

Заряд, находящийся внутри сферы, ищем из формулы:

q = ρ V = ρ 4 3 π r 3 .

Очевидно, что будут происходить изменения напряженности поля внутри шара r ≤ R , согласно выражениям:

E · 4 π r 2 = ρ 4 3 π r 3 ε 1 ε 0 ,

E = ρ r 3 ε 1 ε 0 .

Перейдем к рассмотрению поля вне шара r ≥ R . Для нахождения E ( r ) выбираем сферическую поверхность с радиусом больше радиуса сферы. По теореме Остроградского-Гаусса получим:

E · S = q ε 2 ε 0 , где S обозначает площадь поверхности выделенной сферы. Отсюда следует:

Формула S = 4 π r 2 имеет r ≥ R . Поэтому находящийся внутри заряд выделенной сферы находится из:

q = ρ V = ρ 4 3 π R 3 .

Далее следует подставить площадь из S = 4 π r 2 , заряд из q = ρ V = ρ 4 3 π R 3 , подставив в E · S = q ε 2 ε 0 :

E · 4 πr 2 = ρ 4 3 πR 3 ε 2 ε 0 .

E = ρ R 3 3 ε 2 ε 0 r 2 .

В результате запишем:

E = ρ r 3 ε 1 ε 0 п р и r ≤ R , E = ρ R 3 3 ε 2 ε 0 r 2 п р и r ≥ R .

Ответ: графики показаны на рисунке 1 . Внутри шара напряженность увеличивается прямо пропорционально расстоянию от центра шара. Вне шара она равняется E

1 r 2 . На границе диэлектриков происходит разрыв. Кривая под номером 1 соответствует условию ε 1 > ε 2 .

Предположим, что имеется воображаемая сфера, в центре которой находится точечный заряд. Будет ли изменяться поток вектора напряженности через эту поверхность, если: 1 ) все пространство будет заполнено однородным и изотопным диэлектриком, 2 ) произвести замену сферической поверхности на кубическую?

Решение

По теореме Остроградского-Гаусса поток вектора напряженности через поверхность сферы в пространстве с диэлектриком будет равняться:

Φ E = ∮ S E → d S → = 1 ε 0 q + ∑ j = 1 K q j s v , со значением q j s v в качестве связанных зарядов, которые вызваны поляризацией диэлектрика полем одиночного заряда, q в качестве свободного заряда, находящегося в центре сферы.

Учитывая теорему Остроградского-Гаусса, формула потока вектора напряженности через поверхность сферы в пространстве без диэлектрика примет вид:

Φ E = ∮ S E → d S → = 1 ε 0 q .

Поле было создано при помощи точечного свободного заряда, то при замене формы поверхности потока вектор напряженности не будет изменяться, потому как равняется аналогичным значению заряда, находящегося на поверхности.