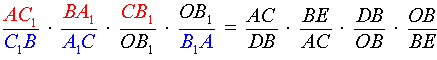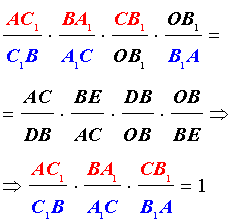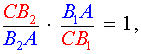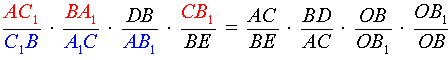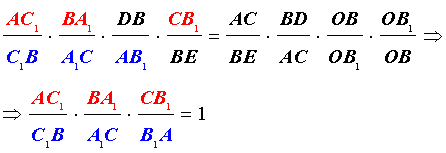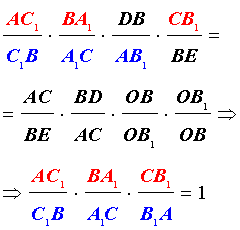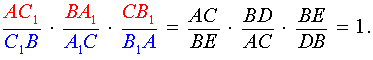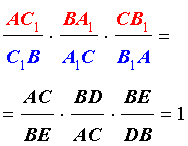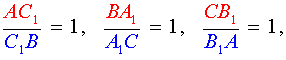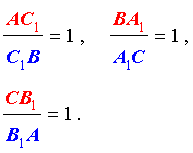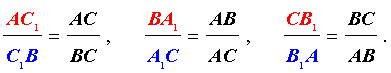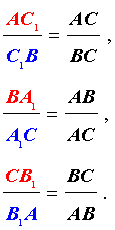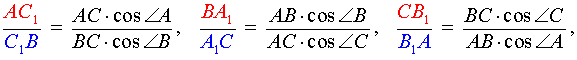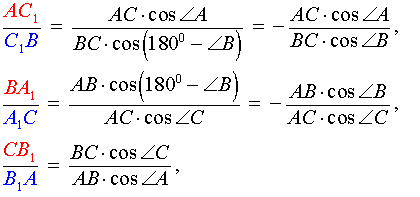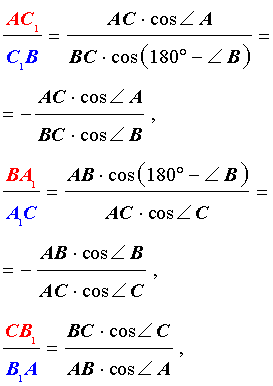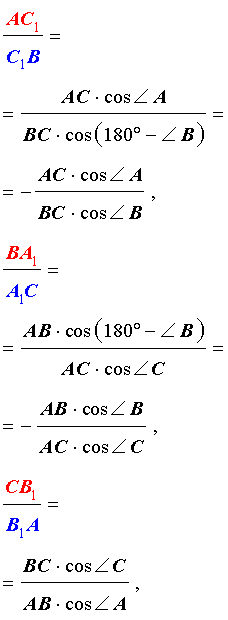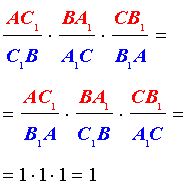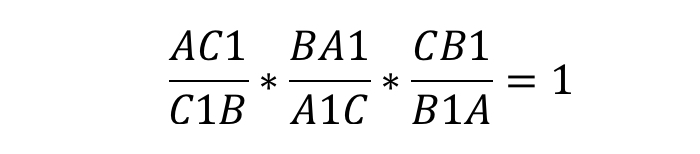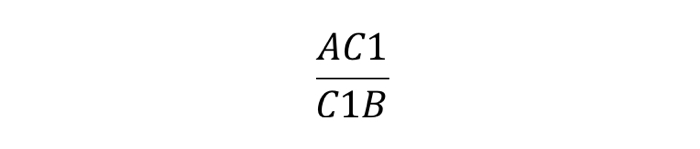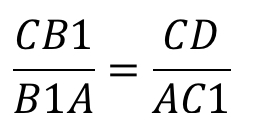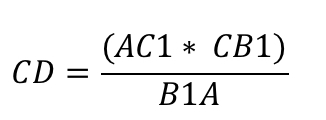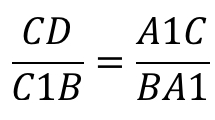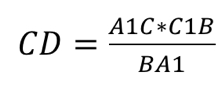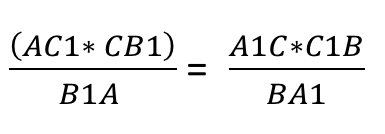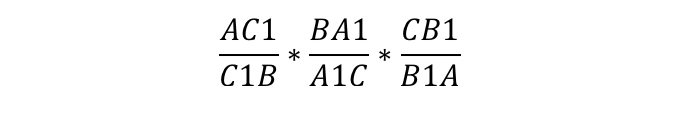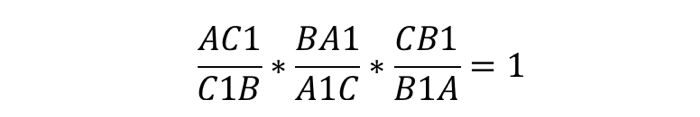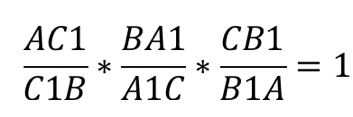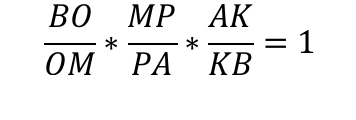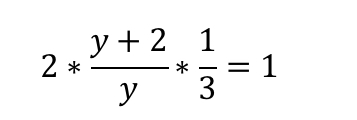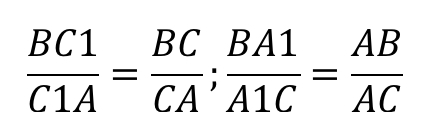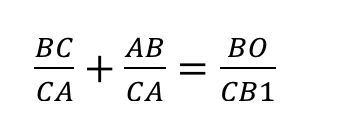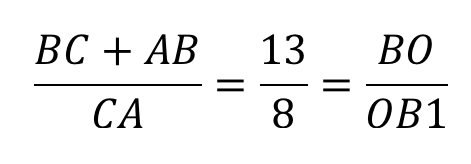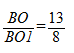Теорема чевы через векторы

Теорема Чевы 1

Теорема Чевы 2

Применения теоремы Чевы

Видео:✓ Теорема Чевы | Осторожно, спойлер! | Борис ТрушинСкачать

Теорема Чевы 1

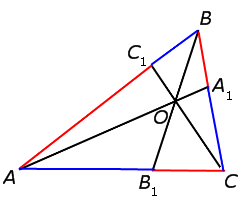
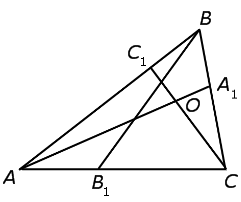
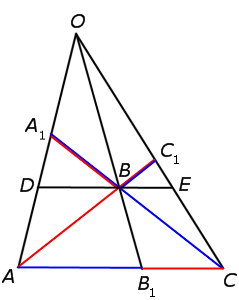
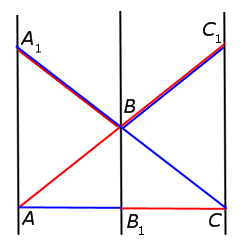
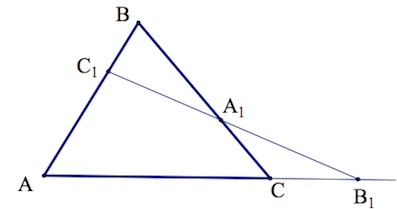
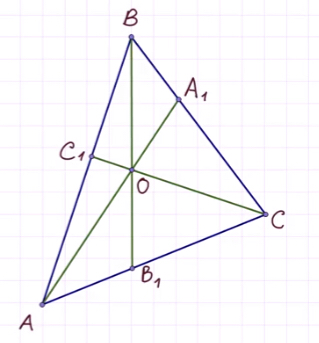
Теорема Чевы 1 . Если на сторонах AB, BC и CA треугольника ABC взяты соответственно точки C₁, A₁ и B₁ (рис.1), то отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке тогда и только тогда, когда выполнено равенство

.

(1)

Доказательство необходимости . Докажем, что, если отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке, то выполнено равенство (1). Для этого проведём через точку B прямую, параллельную прямой AC , и обозначим буквами D и C точки пересечения прямых CC₁ и AA₁ с этой прямой соответственно (рис.2).

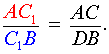(2)

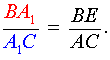(3)

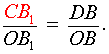(4)

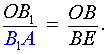(5)

Перемножая равенства (2 – 5), получим

Доказательство необходимости завершено.

Доказательство достаточности . Докажем, что, если выполнено равенство (1), то отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке.

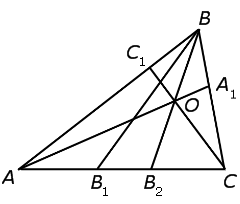
Воспользуемся методом «от противного». С этой целью обозначим буквой O точку пересечения отрезков AA₁ и CC₁ и предположим, что отрезок BB₁ не проходит через точку O (рис. 3).

Проведём через точку O отрезок BB₂ (рис. 4).

Поскольку отрезки AA₁, BB₂ и CC₁ пересекаются в одной точке, то выполнено равенство

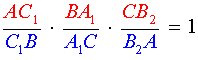(6)

Кроме того, выполнено равенство

(1)

Разделив равенство (6) на равенство (1), получим равенство

следствием которого является равенство

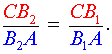(7)

Из равенства (7) вытекает, что точки B₁ и B₂ совпадают.

Доказательство достаточности завершено.

Видео:Теорема ЧевыСкачать

Теорема Чевы 2

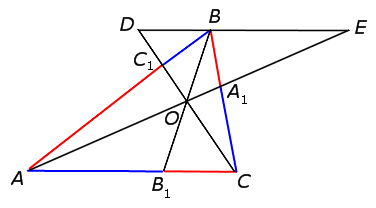
Теорема Чевы 2 . Если на продолжениях за точку B сторон AB и CB треугольника ABC взяты соответственно точки C₁, A₁ , а на стороне CA взята точка B₁ , то прямые AA₁ , BB₁ и CC₁ пересекаются в одной точке или параллельны тогда и только тогда, когда выполнено равенство

.

(8)

Доказательство необходимости (случай «а») . Докажем, что, если прямые AA₁, BB₁ и CC₁ пересекаются в одной точке (рис.5), то выполнено равенство (8). Для этого проведём через точку B прямую, параллельную прямой AC , и обозначим буквами D и C точки пересечения прямых AA₁ и CC₁ с этой прямой соответственно (рис.6).

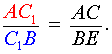(9)

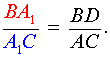(10)

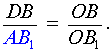(11)

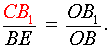(12)

Перемножая равенства (9 – 12), получим

Доказательство необходимости в случае «а» завершено.

Доказательство необходимости (случай «b») . Докажем, что если прямые AA₁, BB₁ и CC₁ параллельны (рис.7), то выполнено равенство (8).

Проведём через точку B прямую, параллельную прямой AС , и обозначим буквами D и E точки пересечения прямых AA₁ и CC₁ с этой прямой соответственно (рис.8).

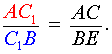(13)

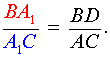(14)

Поскольку четырёхугольники ADBB₁ и BECB₁ параллелограммы, то выполнено равенство

откуда вытекает равенство

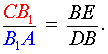(15)

Перемножая равенства (13 – 15), получим

Доказательство необходимости в случае «b» завершено.

Замечание . Доказательство достаточности условия (8) в случае 2 проводится аналогично тому, как это было сделано для случая 1, и мы оставляем его читателю в качестве упражнения.

Видео:Теорема Менелая | Математика | TutorOnlineСкачать

Применения теоремы Чевы

В разделе нашего справочника «Медиана треугольника» доказана теорема о том, что медианы треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим медианы AA₁, BB₁ и CC₁ треугольника ABC (рис.9).

то выполнено равенство

,

откуда вытекает, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема доказана.

В разделе нашего справочника «Окружность, вписанная в треугольник» доказана теорема о том, что биссектрисы треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим биссектрисы AA₁, BB₁ и CC₁ треугольника ABC (рис.10).

В соответствии со свойством биссектрисы справедливы равенства

Если перемножить эти три равенства, то мы получим равенство

,

из которого вытекает, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема доказана.

В разделе нашего справочника «Высота треугольника» доказана теорема о том, что высоты треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим сначала высоты AA₁, BB₁ и CC₁ остроугольного треугольника ABC (рис.11).

то, перемножив эти три равенства, мы получим равенство

,

из которого вытекает, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема о пересечении высот остроугольного треугольника доказана.

Теперь рассмотрим случай тупоугольного треугольника (рис. 12).

На рисунке 12 изображён треугольник ABC с тупым углом B , высотами которого являются отрезки AA₁, BB₁ и CC₁ .

то, перемножив эти три равенства, мы получим равенство

,

из которого вытекает, что прямые AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема о пересечении высот тупоугольного треугольника доказана.

Доказывать теорему о том, что в случае прямоугольного треугольника все высоты пересекаются в одной точке не нужно, поскольку все высоты прямоугольного треугольника пересекаются в вершине прямого угла.

Теорема о пересечении высот треугольника доказана полностью.

Теперь с помощью теоремы Чевы докажем следующую теорему.

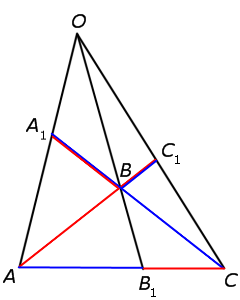
Теорема . Рассмотрим окружность, вписанную в произвольный треугольник ABC . Пусть точки A₁, B₁ и C₁ – точки касания этой окружности со сторонами BC, AC и AB соответственно. Тогда отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке (рис. 13).

Из этих равенств получаем:

Отсюда с помощью теоремы Чевы заключаем, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема доказана.

Замечание . Точку пересечения отрезков AA₁, BB₁ и CC₁ , о которых говорится в только что доказанной теореме, называют точкой Жергонна в честь французского математика Жозефа Жергонна (1771 г. – 1859 г.).

Видео:Теорема ЧевыСкачать

Теорема Чевы и Менелая — формулировка, применение и примеры решения

Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания.

Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.

Именно для этого мы подготовили данный материал. В нем вы узнаете, чем интересны данные основы, принципы их доказательств и рассмотрите решения некоторых задач из ЕГЭ.

Видео:11 класс, 51 урок, Теорема ЧевыСкачать

Формулировка теоремы Менелая

Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.

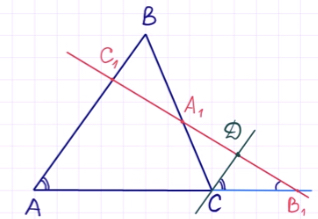
Прежде чем приступить к проработке, сделаем соответствующий рисунок.

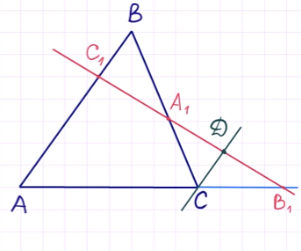
Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.

Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.

Если мы видим приведённый выше рисунок, можно записать формулу:

Запомнить отношение просто: действуем по принципу «вершина — точка, точка — вершина». То есть, если на стороне AB нам дана некоторая точка C1, их отношенное записывается следующим образом:

Доказательство теоремы

Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:

Обозначим точку пересечения данной прямой с B₁C₁ через точку D.

В таком случае мы получим несколько пар подобных треугольников.

Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B₁CD и B₁AC₁. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B₁ между ними.

Углы B₁CD и B₁AC₁ равны как соответственные при параллельных прямых CD, AB и секущей AC.

Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:

Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.

Используя описанное равенства, применив свойства пропорции, запишем:

Запишем следующую пару подобных треугольников: треугольники CDA₁ и BC₁A₁ подобны, так как углы CA₁D и BA₁C₁ равны как вертикальные. Кроме этого, угол CDA₁ равен углу BC₁A₁, как накрест лежащие при параллельных прямых CD, AB и секущей C₁D.

Покажем это на рисунке:

Из данного подобия можно записать некоторую пропорциональность сходственных сторон:

Так же выразим CD:

Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.

Таким образом получаем:

Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:

Что и требовалось доказать.

Видео:#224. Теоремы Менелая, Чевы, Ван-Обеля. Точки Жергонна и НагеляСкачать

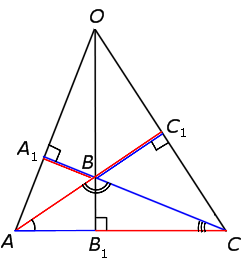
Формулировка теоремы Чевы

Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.

Рассматриваемая теорема была доказана ученым в 1678 г.

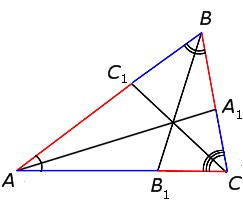
Рассмотрим приведённый ниже рисунок:

Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:

В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами».

Доказательство теоремы

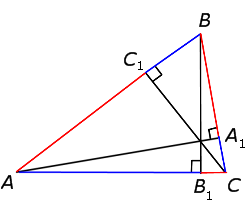
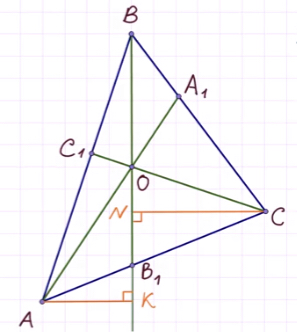
Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.

Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:

Обозначим за O точку пересечения данных прямых.

Продлим медиану BB1.

Проведём перпендикуляры из вершин A и С таким образом:

Треугольники AKB₁ и CNB₁ подобны по острому углу.

Теперь перемножим равенства:

что и требовалось доказать.

Видео:Теорема Менелая. Убийца ГРОБА на ЕГЭ 2020 по профильной математикеСкачать

Применение теорем Чевы и Менелая при решении задач ЕГЭ

Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.

Задача 1

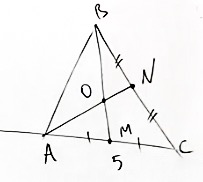
Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.

Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.

AC = 4 см, AM = 2 см.

Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.

Сторону AP обозначим за y.

Найти: чему равен отрезок AP.

Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.

Рассмотрим треугольник ABM. Для него берём прямую OP.

Таким образом мы нашли искомые точки P, A, M, O, K и B.

Запишем теорему Менелая к данному рисунку.

Подставляем в это соотношение известные данные:

В итоге мы получаем, что y = 4.

Ответ: отрезок AP = 4 см.

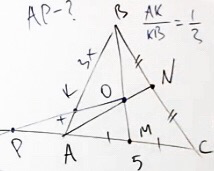
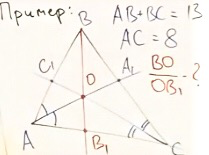
Задача 2

Задача, связанная со свойствами теоремы Чевы.

сумма AB и BC равна 13;

Найти: отношение BO и OB1.

Итак, запишем отношение:

Конечным результатом является дробь 13/8.

Видео:Теорема МенелаяСкачать

Теорема Чевы: формулировка и пример с решением

В данной публикации мы рассмотрим одну из классических теорем аффинной геометрии – теорему Чевы, которая получила такое название в честь итальянского инженера Джованни Чевы. Также разберем пример решения задачи, чтобы закрепить представленный материал.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Формулировка теоремы

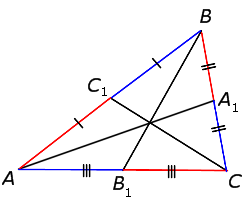
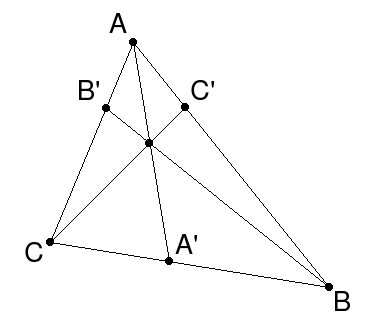
Дан треугольник ABC, в котором каждая вершина соединена с точкой на противоположной стороне.

Таким образом, мы получаем три отрезка (AA’, BB’ и CC’), которые называются чевианами.

Данные отрезки пересекаются в одной точке тогда и только тогда, когда выполняется следующее равенство:

Теорему можно, также, представить в таком виде (определяется, в каком соотношении точки делят стороны):

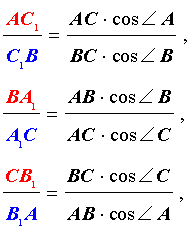
Тригонометрическая теорема Чевы

Примечание: все углы – ориентированные.

Видео:Геометрия: теоремы Менелая, Чевы | Профильная математика ЕГЭ 2023 | УмскулСкачать

Пример задачи

Дан треугольник ABC с точками A’, B’ и C’ на сторонах BC, AC и AB, соответственно. Вершины треугольника соединены с данным точками, и образованные отрезки проходят через одну точку. При этом точки A’ и B’ взяты на серединах соответствующих противоположных сторон. Выясните, в каком соотношении точка C’ делит сторону AB.

Решение
Нарисуем чертеж согласно условиям задачи. Для нашего удобства примем следующие обозначения:

Остается только составить соотношение отрезков согласно теореме Чевы и подставить в него принятые обозначения:

После сокращения дробей получаем:

Значит, AC’ = C’B, т.е. точка C’ делит сторону AB пополам.

Следовательно, в нашем треугольнике отрезки AA’, BB’ и CC’ являются медианами. Решив задачу мы доказали, что они пересекаются в одной точке (справедливо для любого треугольника).

Примечание: с помощью теоремы Чевы можно доказать, что в треугольнике в одной точке, также, пересекаются биссектрисы или высоты.

🔍 Видео

Вебинар 4. Планиметрия. Теоремы Менелая и Чевы в действииСкачать

Теорема Чевы на ЕГЭ 2020? Теорема и задача.Скачать

Теорема ЧевыСкачать

Геометрия, 10 класс | Теорема Менелая. Часть 1Скачать

Он вам не Чева. Теорему забанили на ЕГЭ 2022 по математике. Доказательство теоремы ЧевыСкачать

Теорема МенелаяСкачать

Теорема Чевы с доказательством за 3 МИНУТЫСкачать

Теорема Менелая | Осторожно, спойлер! | Борис Трушин !Скачать

Вебинар 3. Лемма о трезубце. Теорема Менелая, Чевы, Ван - Обеля. Свойства ортоцентра.Скачать

РАЗБИРАЕМ ТЕОРЕМУ МЕНЕЛАЯ ЧАСТЬ II ЧАСТЬ II #shorts #егэ #огэ #математика #профильныйегэСкачать