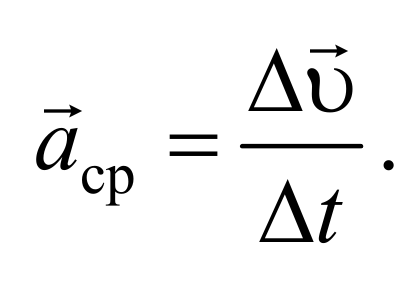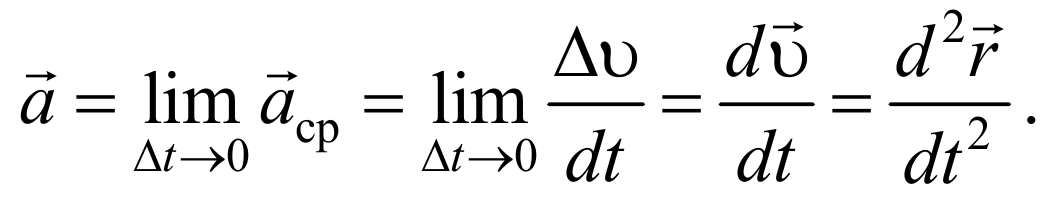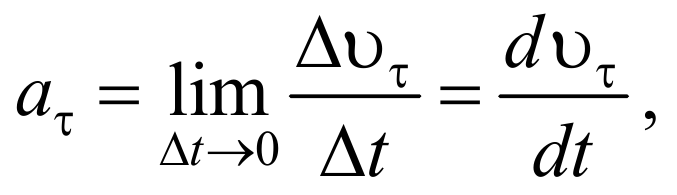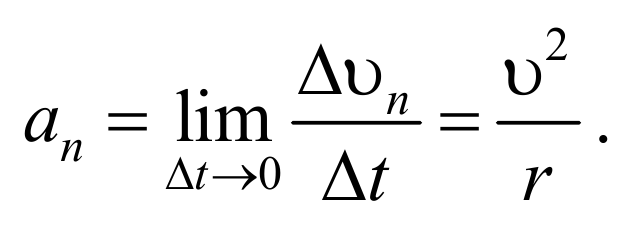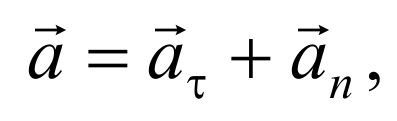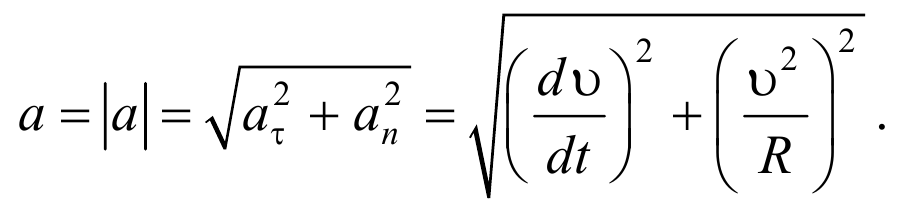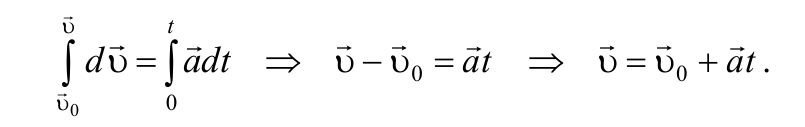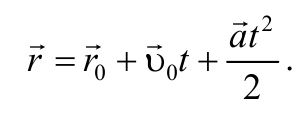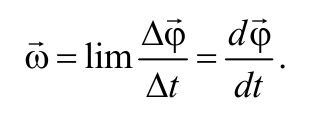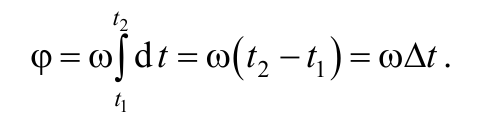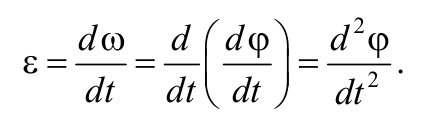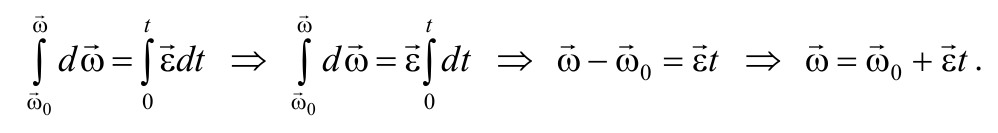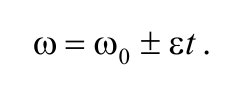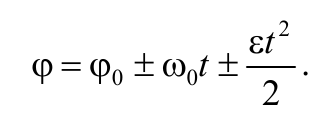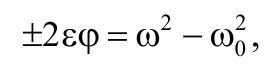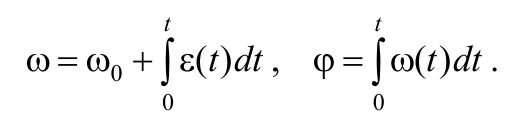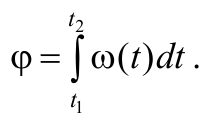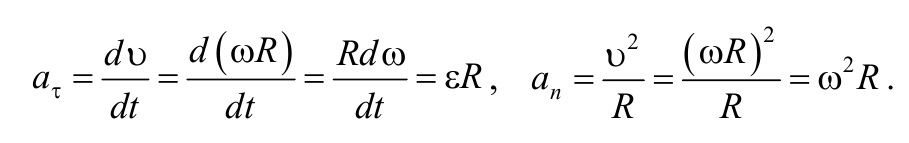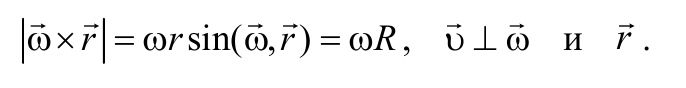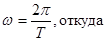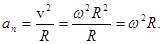- Лекция №2. Элементы кинематики
- 1.4. Нормальное и тангенциальное ускорения при криволинейном движении
- 1.5. Классификация движений материальной точки
- 1.6. Кинематика абсолютно твердого тела
- 1.7. Связь между линейными и угловыми характеристиками тела при его вращении
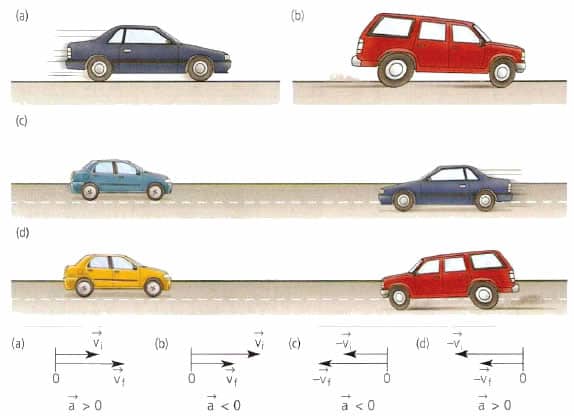
- Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
- Что такое скорость и ускорение?
- Куда направлены векторы ускорения и скорости?
- Действующая на тело сила и ускорение
- Движение по окружности и ускорение
- Тангенциальное ускорение определяется по формуле
- В физике
- Траектория движения и компоненты полного ускорения
- Ускорение тангенциальное
- Ускорение нормальное
- Ускорение полное, нормальное и тангенциальное
- Решение задачи
- Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
- Что такое скорость и ускорение?
- Куда направлены векторы ускорения и скорости?
- Действующая на тело сила и ускорение
- Движение по окружности и ускорение
- Кинематика материальной точки
- Основные формулы кинематики материальной точки
- Радиус-вектор и траектория точки
- Скорость материальной точки
- Касательная к траектории
- Ускорение материальной точки
- Тангенциальное (касательное) и нормальное ускорения
- Тангенциальное (касательное) ускорение
- Радиус кривизны траектории
- Нормальное ускорение
Видео:Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Лекция №2. Элементы кинематики
1.4. Нормальное и тангенциальное ускорения при криволинейном движении
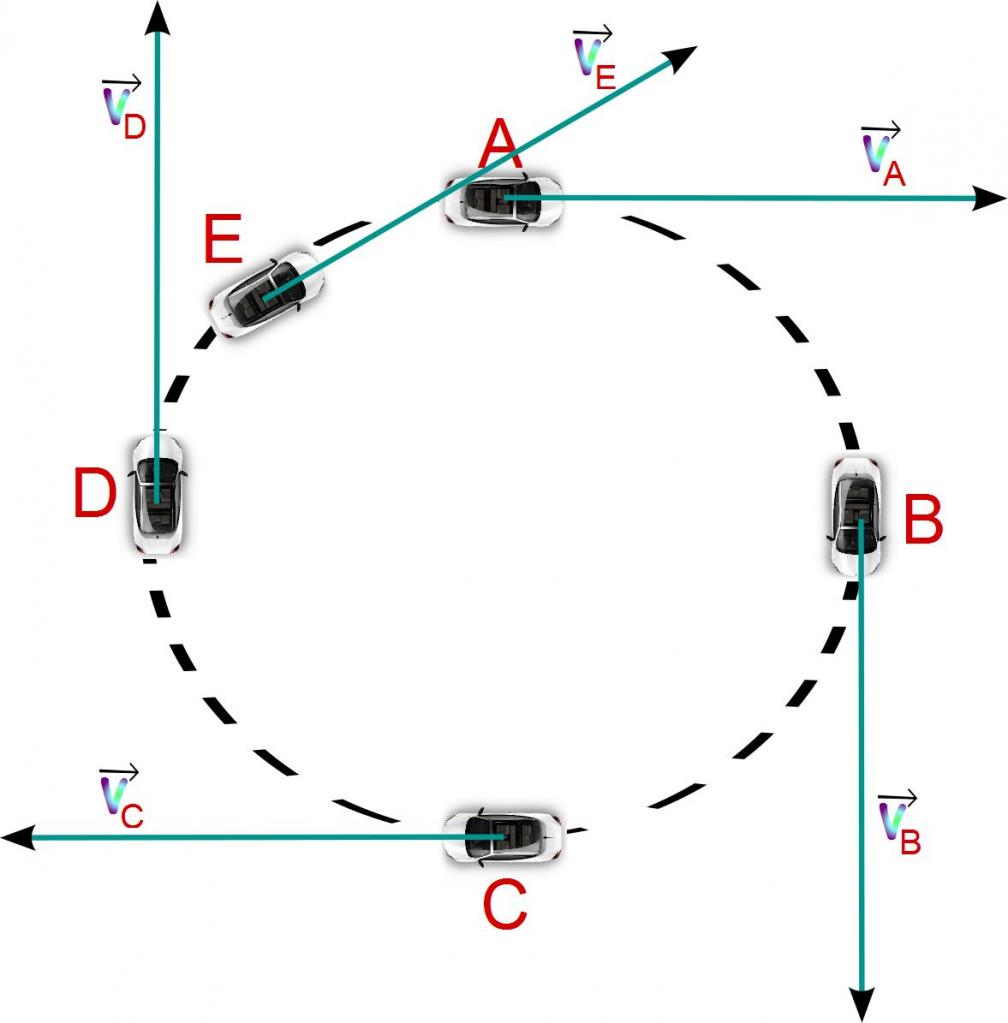
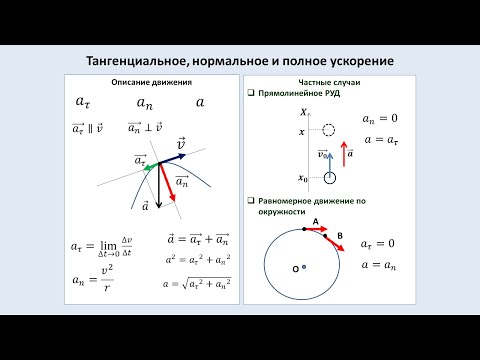
В общем случае при движении тела его скорость изменяется как по величине, так и по направлению. Для характеристики быстроты изменения скорости движения вводится понятие ускорения.
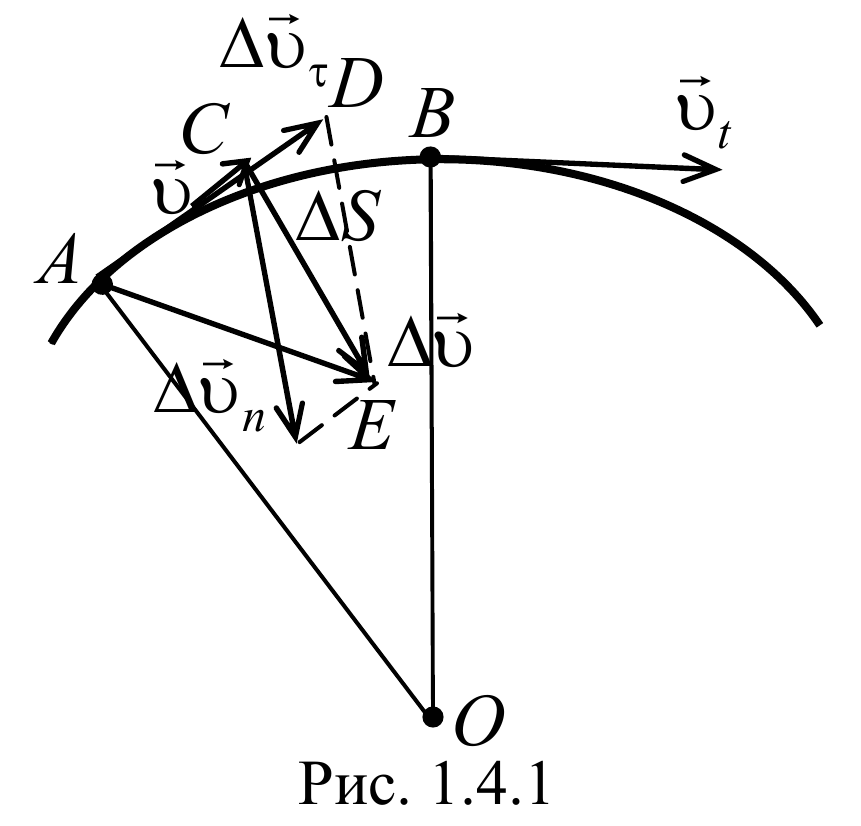
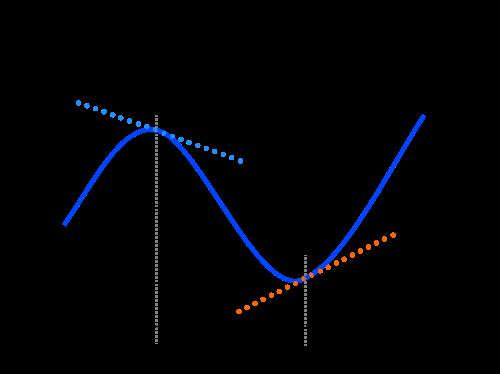
Рассмотрим плоское движение, т. е. такое, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор υ задает скорость точки А , в момент времени t . За время Δt движущаяся точка перешла в положение В и приобрела скорость, отличную от υ как по модулю, так и направлению и равную υ1 = υ +Δ υ . Перенесем вектор υ1 в точку А и найдем Δ υ (рис.). Средним ускорением aср неравномерного движения в интервале времени от t до t+Δt называется векторная величина, равная отношению изменения скорости Δ υ к интервалу времени Δt :
Ускорение в данный момент времени (мгновенное ускорение) представляет собой предел, к которому стремится выражение (1.4.1) при Δt 0 , т. е.
Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.
Разложим вектор Δ υ на две составляющие. Для этого из точки А (рис. 1.4.1) по направлению скорости υ отложим вектор AD , по модулю равный υ1 . Очевидно, что вектор CD , равный Δ υτ , определяет изменение скорости по модулю за время Δt : Δυτ=υ1−υ . Вторая же составляющая Δυn вектора Δ υ характеризует изменение скорости за время Δt no направлению.
Тангенциальная составляющая ускорения
т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Определим вторую составляющую ускорения. Допустим, что точка B близка к точке A , поэтому Δs можно считать дугой окружности некоторого радиуса r , мало отличающейся от хорды AB . Тогда из подобия треугольников AOB и EAD следует Δυn/AB=υ1/r , но так как AB=υΔt , то Δυn/t=υυ1/r . В пределе Δt 0 , получим υ1 υ .
Поскольку υ1 υ , угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол АDE между υ и Δ υn стремится к прямому. Следовательно, при Δt 0 векторы υ и Δ υn оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор Δ υn , перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны. Поэтому эту составляющую ускорения называют также центростремительным ускорением.
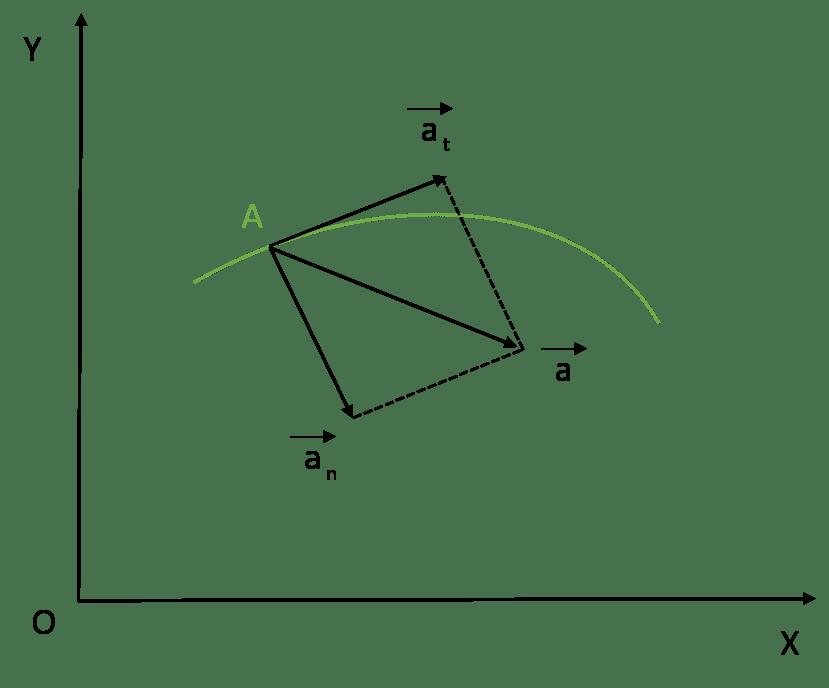
Таким образом, полное ускорение тела a есть геометрическая сумма тангенциальной aτ и нормальной an составляющих
Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.
Нормальное ускорение определяет быстроту изменения скорости по направлению и направлено к центру кривизны траектории.
Векторы aτ и an взаимно перпендикулярны поэтому модуль полного ускорения равен
1.5. Классификация движений материальной точки
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1) aτ=0,an=0 — прямолинейное равномерное движение.
2) aτ=const,an=0 — прямолинейное равнопеременное движение.
Так как $$vec = over dt>$$ , то, проинтегрировав полученное выражение в пределах от нуля до произвольного момента времени можно найти перемещение точки: 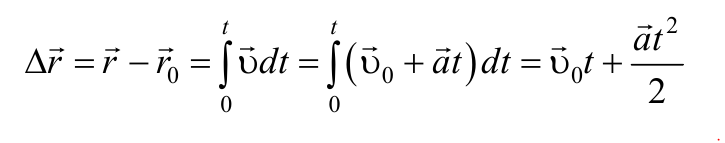
3) aτ= ƒ(t), an=0 − прямолинейное движение с переменным ускорением.
4) aτ=0, an=const — При таком движении скорость точки не изменяется по модулю, так как тангенциальная составляющая равна нулю, а изменяется только по направлению.
5) aτ=const, an≠const − равнопеременное движение по окружности.
6) aτ=0, an≠0 − равномерное криволинейное движение.
7) aτ=const, an≠0 − криволинейное равнопеременное движение.
1.6. Кинематика абсолютно твердого тела
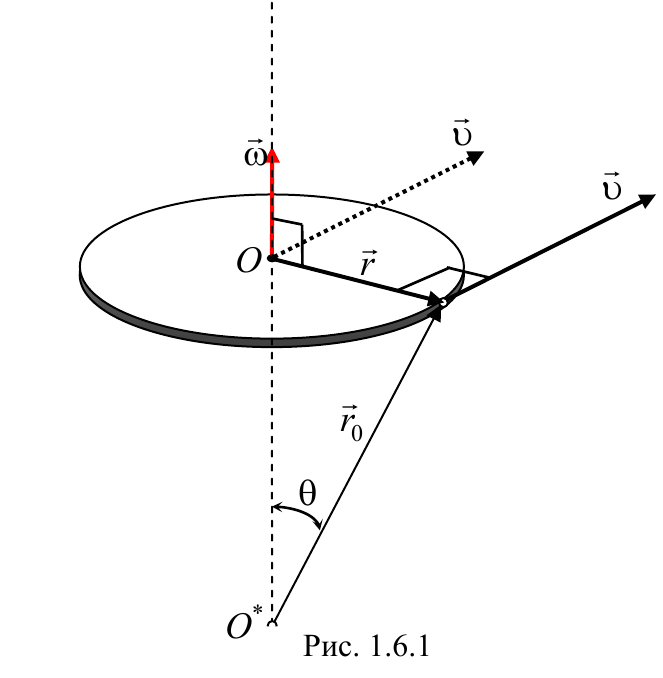
Вращательное движение − это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. При вращательном движении скорости и ускорения различных точек тела неодинаковы. Поэтому в качестве общих кинематических характеристик движения тела при вращении вводятся угол поворота, угловая скорость и угловое ускорение тела. При вращении тела угол поворота изменяется со временем по некоторому закону ϕ = ϕ(t) , который называется уравнением вращательного движения тела.
Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
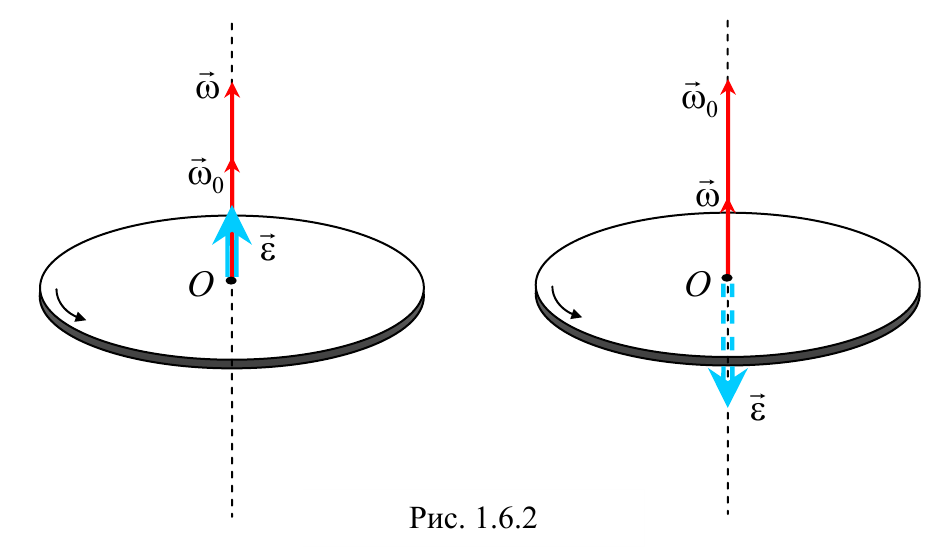
Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1). Единицей угловой скорости является рад/с.
Скорость произвольной точки вращающегося тела называется линейной скоростью этой точки.
При равномерном вращении угловая скорость не изменяется со временем, то есть является постоянной величиной (ω = const) . Тогда
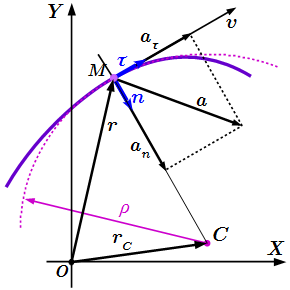
Равномерное вращение характеризуется периодом вращения и частотой вращения.
Период вращения − это время, за которое точка совершает один полный оборот, т. е. поворачивается на угол ϕ = 2π и на основании выражения (1.6.1) $$ = over ω>$$
Частота вращения − это число полных оборотов, которое делает точка при равномерном вращении, за единицу времени: $$ = = $$ , откуда ϕ = 2πn .
Для характеристики неравномерного вращения тела вводится понятие углового ускорения .
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.
В случае равнопеременного движения точки по окружности (ε = const) угловая скорость определяется по формуле
Или в скалярном виде
Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела
Исключив из последнего уравнения t , получим
где φ = 2πN , N − число полное число оборотов, совершенных телом.
В случае ε = ε(t) , угловая скорость и закон вращательного движения определяются следующими формулами
1.7. Связь между линейными и угловыми характеристиками тела при его вращении
За время dt точка проходит по дуге окружности радиуса R путь dS = Rdφ . Поэтому $$ = = = $$ .
Если угол поворота вращающегося тела представить в виде dφ = ω(t)dt и проинтегрировать в пределах от начального момента времени t1 до конечного момента времени t2 , то получится угол, на который совершила поворот тело за время:
Тангенциальная и нормальная составляющие ускорения произвольной точки тела, вращающегося вокруг неподвижной оси, определяются формулами:
Полученные соотношения (1.7.1) можно записать в векторном виде. Для этого на оси вращения ОО* (рис. 1.6.1) тела выберем любую точку A и проведем из нее радиус-вектор r в точку M . Векторное произведение ω × r по модулю и направлению совпадает с вектором скорости υ точки M :
Следовательно, можно записать, что вектор скорости υ = ω × r , а вектор ускорения точки
Видео:Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать
Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.
Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Что такое скорость и ускорение?
Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:
Здесь вектор l¯ направлен от начальной точки пути к конечной.
В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:
Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.
Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.
Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Куда направлены векторы ускорения и скорости?
В физике всякое механическое движение тела принято характеризовать определенной траекторией. Последняя представляет собой некоторую воображаемую кривую, вдоль которой тело перемещается в пространстве. Например, прямая линия или окружность — это яркие примеры распространенных траекторий движения.
Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.
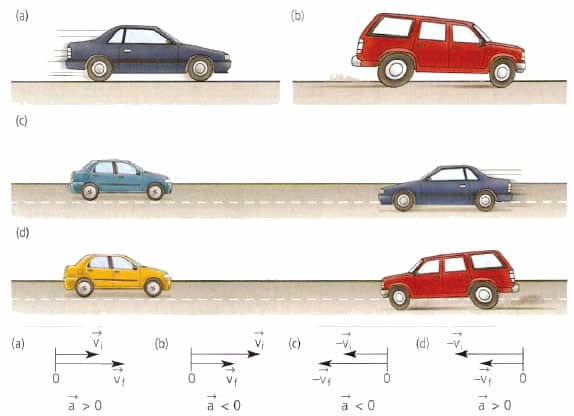
Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.
Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Действующая на тело сила и ускорение
Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.
Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:
Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.
Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.
Видео:Нормальное и тангенциальное ускорение [Физзадачи #37]Скачать
![Нормальное и тангенциальное ускорение [Физзадачи #37]](https://i.ytimg.com/vi/HTVGtCaQgEk/0.jpg)
Движение по окружности и ускорение
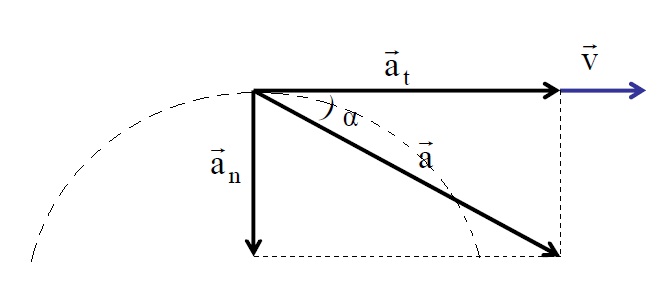
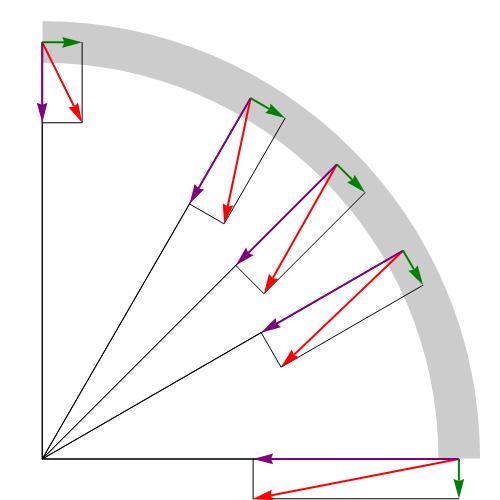
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.
Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.
Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.
Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.
Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.
Видео:Центростремительное ускорение. 9 класс.Скачать

Тангенциальное ускорение определяется по формуле
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
Нормальное ускорение 
Здесь R – это радиус кривизны траектории в заданной точке.
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

Нормальное, тангенциальное и полное ускорение
Ускорение при криволинейном движении
В случае движения материальной точки по криволинейной траектории различают нормальное и тангенциальное ускорения.
Нормальное (центростремительное) ускорение 
Модуль нормального ускорения определяют по формуле 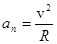
Тангенциальное (касательное) ускорение 
Модуль тангенциального ускорения определяют по формуле 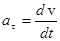
Модуль полного ускорения 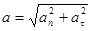
Тело, деформациями которого в данных условиях движения, можно пренебречь называют абсолютно твердым телом.
При вращательном движении радиус-вектор каждой точки поворачивается за одно и то время 
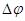
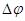
Угловой скоростью тела называют величину
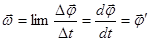
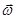
Равномерное вращение характеризуется периодом обращения Т.
Периодом обращения называют промежуток времени, за которое тело делает один полный оборот (поворачивается на угол 2π).
Модуль угловой скорости равномерного движения

Частотой обращения называют число оборотов точки за единицу времени 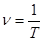
Таким образом,
Угловое ускорение характеризует быстроту изменения угловой скорости (в случае неравномерного вращения)

Линейная скорость тела связана с угловой соотношением 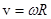
Модуль нормального ускорения
Модуль тангенциального ускорения 
Дата добавления: 2014-11-18 ; Просмотров: 889 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

В физике
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2 ).
Видео:Лекция по физике №1. Прямолинейное движение. Вектор скорости. Тангенциальное и нормальное ускорение.Скачать

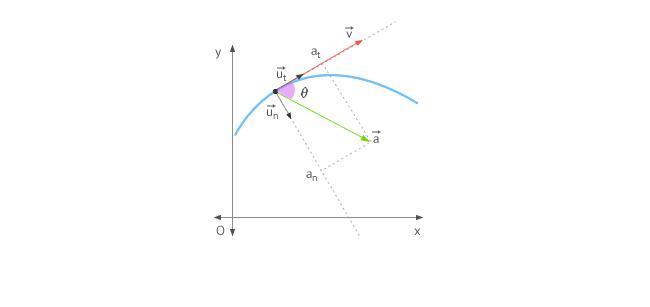
Траектория движения и компоненты полного ускорения
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
Здесь ut¯ – вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
Видео:Скорости и ускорения точек вращающегося телаСкачать

Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
Это выражение позволяет описать свойства величины at¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения – это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Видео:Нормальное и тангенциальное ускорениеСкачать

Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
Здесь dL – это пройденный телом путь за промежуток времени dt, r – радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Видео:Что такое тангенциальное ускорение #shorts #ЕНТ #ЕНТ_по_физике #Умскул #НиколайАкуловСкачать

Ускорение полное, нормальное и тангенциальное
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Видео:Хитрый способ нахождения тангенциального и нормального ускорений: Волькенштейн 1.19Скачать

Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
Для тангенциального имеем:
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
Теперь можно воспользоваться формулой для an:
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Что такое скорость и ускорение?
Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:
Здесь вектор l¯ направлен от начальной точки пути к конечной.
В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:
Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.
Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.
Видео:A.2.15 Построение совершенных дизъюнктивной и конъюнктивной нормальных форм (СДНФ и СКНФ)Скачать

Куда направлены векторы ускорения и скорости?
В физике всякое механическое движение тела принято характеризовать определенной траекторией. Последняя представляет собой некоторую воображаемую кривую, вдоль которой тело перемещается в пространстве. Например, прямая линия или окружность — это яркие примеры распространенных траекторий движения.
Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.
Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.
Видео:Вращательное движение. 10 класс.Скачать

Действующая на тело сила и ускорение
Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.
Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:
Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.
Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.
Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Движение по окружности и ускорение
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.
Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.
Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.
Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.
Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.
Видео:ТММ - 5.1, 5.2 Кинематический анализ. Метод планов.Скачать

Кинематика материальной точки
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Основные формулы кинематики материальной точки
Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.
Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .
Скорость точки:
;
;
;
Единичный вектор в направлении касательной к траектории точки:
.
Вектор можно выбрать двумя способами во взаимно противоположных направлениях. Обычно его выбирают в направлении увеличения дуговой координаты. Тогда, наряду с модулем скорости , вводят алгебраическую величину скорости . При , вектор скорости сонаправлен с . При – имеет противоположное с направление.
Тангенциальное (касательное) ускорение:
;
;
.
Здесь, как и для скорости, – это алгебраическое касательное ускорение, . Если , то вектор касательного ускорения сонаправлен с . При – имеет противоположное с направление.
Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.
Радиус кривизны траектории:
.
Далее приводится вывод этих формул и изложение теории кинематики материальной точки.
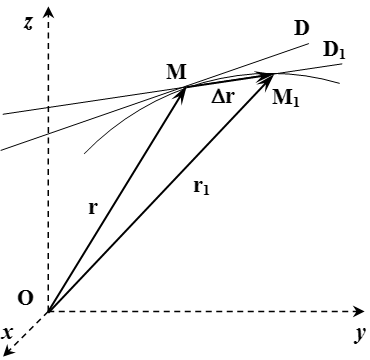
Радиус-вектор и траектория точки
Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.
Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .
При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.
Траектория материальной точки – это линия, вдоль которой происходит движение точки.
Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями
В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .
Скорость материальной точки
Согласно определению скорости и определению производной:
Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:
,
где
,
,
– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.
Таким образом
.
Модуль скорости:
.
Касательная к траектории
С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .
При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.
Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.
Здесь мы направили вектор по направлению к вектору скорости, поскольку это более удобно. Но могут возникнуть случаи, когда точка останавливается и движется по той же траектории в обратном направлении. Чтобы не вводить для одной и той же точки траектории два единичных касательных вектора, нужно охватить случай, когда направлен противоположно скорости. Для этого вводят алгебраическую величину скорости:
.
Если направления векторов и совпадают, то . Если они противоположны, то .
– это проекция скорости на направление единичного вектора . Она равна скалярному произведению этих векторов:
.
Абсолютную величину (модуль) вектора скорости мы обозначаем символом с прямыми скобками, или символом без стрелки:
;
Алгебраическая величина скорости:
.
Тогда вектор скорости точки можно представить в следующем виде:
.
Ускорение материальной точки
Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.
Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают их скалярное произведение. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.

Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к ней.
Тангенциальное (касательное) ускорение
Также как и для скорости, введем алгебраическую величину вектора касательного ускорения :
.
Если , то вектор касательного ускорения сонаправлен с . Если , то эти векторы противоположны. Абсолютную величину касательного ускорения будем обозначать прямыми скобками: . Тогда
.
Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили: .
Отсюда видно, что алгебраическая величина тангенциального ускорения равна проекции полного ускорения на направление касательной к траектории. Она также равна производной по времени алгебраической величины скорости точки: .
Подставив , имеем:
.
Здесь мы учли, что .
Найдем производную по времени модуля скорости . Применяем правила дифференцирования:
;
.
Итак,
.
Отсюда следует, что если между векторами ускорения и скорости острый угол: , то движение ускоренное. Абсолютное значение скорости возрастает. Если между ними тупой угол: , то движение замедленное. Абсолютное значение скорости убывает.
Выразим ускорение через тангенциальное и нормальное: , и учтем, что . Получим:
.
Тогда предыдущую формулировку можно выразить посредством тангенциального ускорения. Если векторы касательного ускорения и скорости направлены в одну сторону, то движение ускоренное. Если их направления противоположны, то движение замедленное.
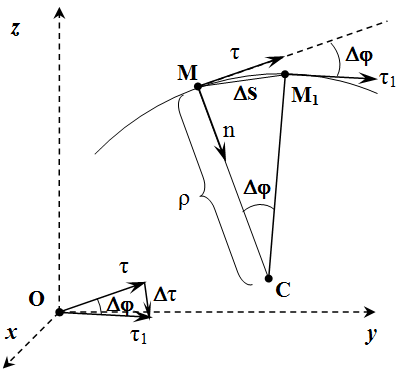
Радиус кривизны траектории
Теперь исследуем вектор .
Рассмотрим вектор в два момента времени – в момент времени t и в момент t 1 . Введем обозначения: . По определению производной:
.
Пусть в момент времени t , точка находится в положении M , а в момент t 1 – в положении M 1 (см. рисунок).
Рассмотрим случай, когда алгебраическая скорость положительна: . То есть направления векторов и совпадают. Тогда точка M 1 находится справа от M . Через точки и проведем плоскости, перпендикулярные векторам и . Пересечение этих плоскостей образует прямую. Она проходит через точку C перпендикулярно плоскости рисунка. MC – это перпендикуляр, опущенный из точки M на эту прямую.
При , точка стремится к точке , а длина отрезка CM стремится к радиусу кривизны траектории ρ . Поскольку и , то угол между отрезками и равен углу между векторами и . Отложим их для наглядности из одного центра.
Абсолютное значение производной:
.
Здесь мы учли, что .
Вектор , как указывалось выше, перпендикулярен . В данном случае он направлен вдоль единичного вектора главной нормали , направленной к центру кривизны C траектории. Поэтому при имеем:
.
Теперь рассмотрим случай, когда алгебраическое значение скорости отрицательно: . В этом случае, вектор скорости противоположен . Получается тот же рисунок, только точка располагается слева от M . В результате абсолютное значение производной остается прежней:
.
Но ее направление меняется на противоположное:
.
Поскольку , то формула сохраняет прежний вид и в этом случае:
.
Нормальное ускорение
Теперь находим нормальное ускорение:
.
Перепишем результат в следующем виде:
,
где ; – единичный вектор в направлении главной нормали траектории – то есть вектор, направленный к мгновенному центру кривизны перпендикулярно касательной к траектории. Поскольку , то также является модулем нормального ускорения. Для него не нужно вводить алгебраическое значение, как мы это делали для скорости и касательного ускорения.
Нормальное ускорение всегда направлено к центру кривизны траектории.
Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.
Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.
Выпишем еще раз следующую формулу:
.
Отсюда видно, что нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.
Радиус кривизны траектории:
.
И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.
Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.
Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 27-01-2020