- Арктангенс, arctg
- Определение и обозначения
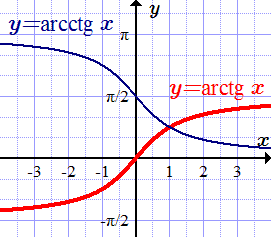
- График функции арктангенс
- Арккотангенс, arcctg
- Определение и обозначения
- График функции арккотангенс
- Четность
- Свойства – экстремумы, возрастание, убывание
- Таблица арктангенсов и арккотангенсов
- Формулы
- Формулы суммы и разности
- Выражения через логарифм, комплексные числа
- Выражения через гиперболические функции
- Производные
- Интегралы
- Разложение в степенной ряд
- Обратные функции
- Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
- Значения арксинуса, арккосинуса, арктангенса и арккотангенса
- Основные значения arcsin, arccos, arctg и arctg
- Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
- Нахождение значения arcsin, arccos, arctg и arcctg
- Арктангенс и арккотангенс. Онлайн калькулятор
- Арктангенс и арккотангенс − теория, примеры и решения
- Функция арктангенс и ее график
- Функция арккотангенс и ее график
- 📹 Видео
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Арктангенс, arctg
Определение и обозначения
Арктангенс обозначается так:
.
График функции арктангенс
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Арккотангенс, arcctg
Определение и обозначения
Арккотангенс обозначается так:
.
График функции арккотангенс
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Видео:Преобразование выражений, содержащих арксинус, арккосинус, арктангенс и арккотангенс. 2 ч. 10 класс.Скачать

Четность
Функция арктангенс является нечетной:
arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x ≠ ± arcctg x .
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Свойства – экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | – ∞ | – ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
| – | π | |
| 0 |
Видео:Отбор арктангенса по окружности | Тригонометрия ЕГЭ 2020Скачать

Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
Видео:Занятие 7. Арктангенс и арккотангенс. Основы тригонометрииСкачать

Формулы
Формулы суммы и разности
при
при 0,;xy > 1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-138px -570px»>
при 1″ style=»width:122px;height:18px;vertical-align:-10px;background-position:-261px -570px»>
при -1″ style=»width:76px;height:18px;vertical-align:-10px;background-position:-550px -570px»>
при 0,;xy
при
Видео:Занятие 4. Арксинус и арккосинус. Основы тригонометрииСкачать

Выражения через логарифм, комплексные числа
Видео:Находим арктангенс. Алгебра 10 классСкачать

Выражения через гиперболические функции
Видео:Арксинус, арккосинус, арктангенс и арккотангенс числа . Тригонометрия . 10 класс .Скачать

Производные
Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
Аналогично для арккотангенса. Пусть . Тогда
;
.
Видео:Алгебра 10 класс. 18 октября. Что такое arccos арккосинусСкачать

Интегралы
Делаем подстановку x = tg t и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Видео:Обратные тригонометрические функции, y=arcsinx и y=arccosx, их свойства и графики. 10 класс.Скачать

Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg x ) = x
ctg(arcctg x ) = x .
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x ) = x при
arcctg(ctg x ) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 14-07-2014 Изменено: 23-12-2018
Видео:Арк-функции. Простейшие тригонометрические уравнения | Осторожно, спойлер! | Борис Трушин !Скачать

Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Видео:Вычисление аркфункцийСкачать

Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin ( — π 2 ) = — 1 , sin ( — π 3 ) = — 3 2 , sin ( — π 4 ) = — 2 2 , sin ( — π 6 ) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | |
| a r c sin α к а к у г о л | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
| в г р а д у с а х | — 90 ° | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c sin α к а к ч и с л о | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1
Следуя из таблицы, находим значения арккосинуса:
a r c cos ( — 1 ) = π , arccos ( — 3 2 ) = 5 π 6 , arcocos ( — 2 2 ) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | 1 | |
| a r c cos α к а к у г о л | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 | |
| в г р а д у с а х | 180 ° | 150 ° | 135 ° | 120 ° | 90 ° | 60 ° | 45 ° | 30 ° | 0 ° | |
| a r c cos α к а к ч и с л о | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 | |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Видео:Отбор корней с аркфункциями в №12 | Это будет на ЕГЭ 2023 по математикеСкачать

Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Видео:Что такое арктангенс и арккотангенсСкачать

Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:
a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Арктангенс и арккотангенс. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Преобразование выражений, содержащих арккосинус, арксинус, арктангенс и арккотангенс. 1ч. 10 класс.Скачать

Арктангенс и арккотангенс − теория, примеры и решения
Функция арктангенс и ее график
Функция тангенс определена в интервале [−∞;+∞] кроме точек 

 |
Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
 , ,  , ,  , ,  и т.д. и т.д. |
По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
| y=arctg x. | (1) |
Функция (1) − это функция, обратная к функции
 . . |
График функции арктангенс можно получить из графика функции 
 |
Свойства функции арктангенс.
- Область определения функции:
.
- Область значений функции:
.
- Функция является нечетной:
.
- Функция возрастает.
- Функция непрерывна.
Решим тригонометрическое уравнение
В интервале 
Следовательно в интервале 
 . . | (3) |
Решение уравнения (2) представлен на Рис.3:
 |
Так как tg t − это ординат точки пересечения прямой OMt1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OTt пересекается с окружностью с радиусом 1 в двух точках: 



Пример 1. Решить тригонометрическое уравнение:
 . . |
Решение. Воспользуемся формулой (3):
 , , |
 . . |
Пример 2. Решить тригонометрическое уравнение:
 . . |
Решение. Воспользуемся формулой (3):
 . . |
Используя онлайн калькулятор получим:
 . . |
Функция арккотангенс и ее график
Как известно, функция котангенс определена в интервале [−∞;+∞] кроме точек -2π, —π 0, π, 2π. и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
 |
Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
  |
По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
| y=arcctg x. | (4) |
Функция (4) − это функция, обратная к функции
 . . |
График функции арккотангенс можно получить из графика функции 
 |
Свойства функции арккотангенс.
- Область определения функции:
.
- Область значений функции:
.
- Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
- Функция убывает.
- Функция непрерывна.
Решим тригонометрическое уравнение
В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:
 | (6) |
Решения уравнения (5) можно представить на единичной окружности (Рис.6):
 |
ctg t − это абсцис точки пересечения прямой 





Пример 1. Решить тригонометрическое уравнение:
 . . |
Решение. Воcпользуемся формулой (6):
 . . |
Так как в интервале (0; π)
 . . |
Пример 2. Решить следующее тригонометрическое уравнение:
 . . |
Решение. Используя формулу (6), имеем
 . . |
С помощью онлайн калькулятора вычисляем 
📹 Видео
Определение арктангенса,арккотангенсаСкачать







 .
. .
. .
. .
.