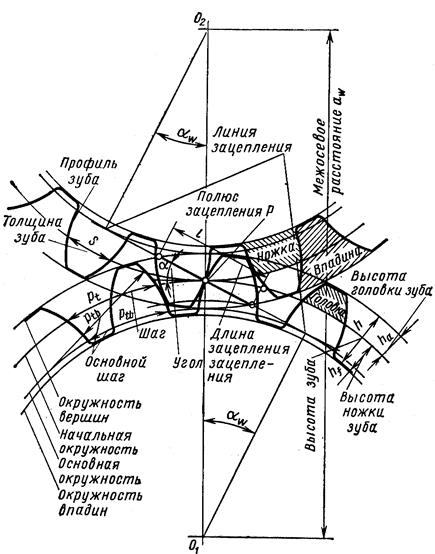
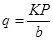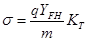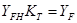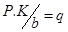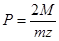Как определить диаметр окружности вершин зубьев (4 видео)

Расчет основных геометрических параметров цилиндрических прямозубых колес

Эвольвентное зацепление двух зубчатых колес характеризуется следующим параметрами (ГОСТ 16530-70) (рис. 13.3).

Начальные окружности (d_w₁ и d_w₂) – воображаемые окружности, которые в процессе работы передачи перекатываются одна по другой без скольжения. Начальные окружности появляются у зубчатых колес в собранной передаче. Для отдельно взятого колеса понятие начальной окружности отсутствует. Оно имеет делительную окружность.

Окружность вершин зубьев (d_α) – окружность ограничивающая головки зубьев.

Окружность впадин (d_f) – окружность, проходящая через основания впадин зубьев.

Основная окружность (d_b₁ и d_b₂) – окружность, при развертке которой получается эвольвента.

Делительная окружность (d₁ и d₂) – окружность зубчатого колеса, по которой обкатывается делительная окружность (прямая) инструмента в процессе нарезания зубьев. Делительная окружность колеса является начальной только в процессе изготовления (нарезания) зубьев. У некорригированных колес и при высотной коррекции начальные и делительные окружности совпадают.

Полюс зацепления (точка “P”) – точка касания начальных окружностей.

Рис. 13.3. Элементы зубчатого зацепления

Окружной шаг зацепления (P_t) – расстояние между одноименными профилями, измеренное по дуге делительной окружности, зубчатого колеса.

Головка зуба (h_α) – часть зуба между делительной окружностью зубчатого колеса и его окружностью вершин зубьев.

Ножка зуба (h_f) – часть зуба между делительной окружностью и его окружностью впадин.

Высота зуба (h) равна сумме высот головки и ножки зуба.

Дуга зацепления (l) – путь по начальной окружности, проходимой точкой профиля за время зацепления пары сопряженных зубьев.

Коэффициент перекрытия (ε) – отношение дуги зацепления к окружному шагу.

Линия зацепления (N₁ и N₂) – линия, по которой перемещается точка касания зубьев. Линия зацепления проходит через полюс зацепления и является касательной к основным окружностям.

Угол зацепления (α_w) – угол между линией зацепления и касательной к начальным окружностям в полюсе зацепления.

Модуль зацепления (m). Все модули стандартизованы в пределах от 0,05 мм до 100 мм.

Рассмотренные параметры составляют определенные кинематические зависимости. В табл. 10 приводятся основные соотношения для цилиндрических некорригированных зубчатых передач внешнего зацепления.

В расчётах зуб зубчатого колеса рассматривают как балку, защемленную одним концом и нагруженную силой (Q_n). Такое положение нагрузки принимается как наиболее опасное.

Наиболее опасное сечение, где наиболее вероятен излом зуба, находится у его корня в зоне наибольшей концентрации напряжений. Максимальное напряжение возникает на стороне сжатия (нерабочая сторона). Однако следует отметить то, что расчет на прочность необходимо производить по напряжению на рабочей стороне, т.к. на этой растянутой стороне зуба здесь может образоваться усталостная трещина.

Основные соотношения для цилиндрических
некорригированных зубчатых передач внешнего зацепления

Параметры зацепления	Формулы
Окружной модуль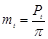
Нормальный модуль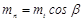
Нормальный шаг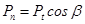
Межосевое расстояние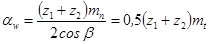
Высота головки зуба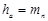
Высота ножки зуба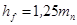
Высота зуба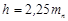
Радиальный зазор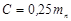
Делительный диаметр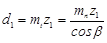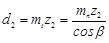
Начальный диаметр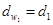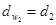
Диаметр основной окружности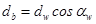
Диаметр вершин зубьев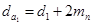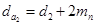
Диаметр впадин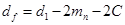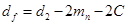
Коэффициент перекрытия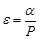

13.3. Расчет зубьев
цилиндрических прямозубых зубчатых колес на изгиб

— для обозначения расчета на изгиб, который проводится по ножке зуба принят индекс F (от термина ножка – Fut – на английском и немецком языках).

— для обозначений расчета на контактную прочность принят индекс H, в честь автора теории расчетов контактных напряжений Г. Герца.

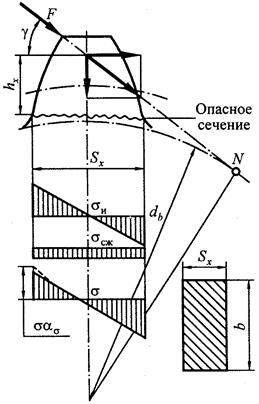
Расчет ведется по расчетной окружной силе (q), отнесенной к единице ширины венца.

где: P – передаваемое окружное усилие;

b – ширина венца зубчатого колеса (длина зуба);

K – коэффициент нагрузки, учитывающий дополнительные вредные явления (удары).

q – расчетная окружная сила, отнесенная к единице ширины венца (b).

Нормальная удельная сила равна:

Перенесем силу давления q_n вдоль линии ее действия (линия зацепления) в точку, расположенную на оси симметрии зуба (рис. 13.4) и разложим на две составляющие: изгибающую зуб (q_ncosα_n), вызывающую в опасном сечении напряжения изгиба (σ_u) и сжимающую зуб (q_nsinα), вызывающую в зубе напряжения сжатия (σ_c_ж). Угол «γ» несколько больше угла профиля «α_w» (γ = α_w = 20˚).

Номинальное напряжение в опасном сечении:

;
;

;
;
.

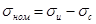
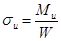
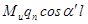
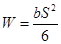
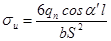
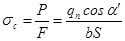
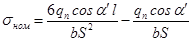
Рис. 13.4. Схема расчета зубьев на изгиб

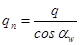
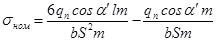
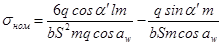
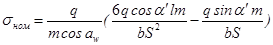
Умножим числитель и знаменатель на модуль «m» и заменим получим:

;

приняв: ;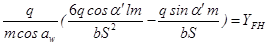

получим: .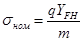

;

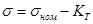
обозначив:

получим: ,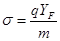

где: K_T – теоретический коэффициент концентрации напряжений;

Y_FHU, Y_F – коэффициенты прочности зубьев соответственно по номинальным и местным напряжениям;

Y_FH – представляет собой номинальное напряжение в опасном сечении зуба при m = 1 и q = 1, а Y_F – местное напряжение при тех же условиях.

Технические расчеты удобно вести по формулам, в которых условия нагружения заданы в форме номинальных крутящих моментов М (ктс.см) или мощности (кВт), частоты вращения n (об/мин) и коэффициента нагрузки К.

;

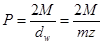
Для технических проверочных расчетов следует умножить P.K и приняв

получим: ;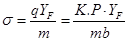

если

то: .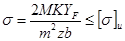

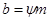
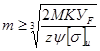
Модуль и ширина зубчатого венца, прежде всего, определяют прочность зуба на изгиб. Приняв и решив последнее уравнение относительно модуля, после преобразований получим:

Наиболее рациональной формой расчет, обеспечивающей равнопрочностъ зубьев по выкрашиванию и излому, является определение модуля по известному межосевому расстоянию “a_w” и ширине зубчатого венца “b” полученным из расчета на конкретную прочность.

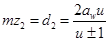
После преобразования получим:

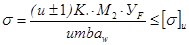
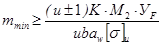
Для большинства редукторов общего назначения:

;

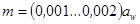
коэффициент нагрузки К можно выразить:

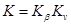
здесь: K_β – коэффициент концентрации нагрузки;

K_v – коэффициент динамичности нагрузки.

Содержание

Как определить диаметр окружности вершин зубьев
Диаметр основной окружности зубчатого колеса
Делительный диаметр d = 6∙12 = 72 мм.
Основной диаметр db = 6∙12∙cos20 ˚ = 67,66 мм.
Диаметр окружности вершин da = 6∙(12 + 2 + 2∙0,5 – 2∙0,07) = 89,16 мм.
Понятие об исходном контуре рейки
📸 Видео

Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Как определить диаметр окружности вершин зубьев

Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. При проектировании зубчатого колеса вначале нужно определить его число зубьев z , а затем определить параметры зубьев. Для этого нужно произвольную окружность колеса r y разделить на z частей, каждая из которых называется окружным шагом p y .

где m y = p y / p = d y / z — модуль зацепления по окружности произвольного радиуса.

Как определить диаметр окружности вершин зубьев

Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p . В зависимости от окружности по которой определен модуль различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) — число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого модуль можно определить как число милиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по окружности называемой делительной. Точнее делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба). Угловой шаг t — центральный угол соответствующий дуге p — окружному шагу по делительной окружности.

Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины — строчными буквами латинского алфавита, угловые — греческими буками; установлены индексы для величин :

по окружностям: делительной — без индекса, вершин — a , впадин — f , основная — b , начальная — w , нижних точек активных профилей колес — p , граничных точек — l ;

по сечениям: нормальное сечение — n , торцевое сечение — t , осевое сечение — x ;

относящихся к зуборезному инструменту — 0 .

Для параметров зубчатого колеса справедливы следующие соотношения

— диаметр окружности произвольного радиуса,

— диаметр делительной окружности,

— шаг по окружности произвольного радиуса,

— шаг по делительной окружности,

где a — угол профиля на делительной окружности,

a y — угол профиля на окружности произвольного радиуса.

Углом профиля называется острый угол между касательной к профилю в данной точки и радиусом — вектором, проведенным в данную точку из центра колеса.

Шаг колеса делится на толщину зуба s y и ширину впадины e y . Толщина зуба s y — расстояние по дуге окружности r y между разноименными точками профилей зуба. Ширина впадины e y — расстояние по дуге окружности r y между разноименными точками профилей соседних зубьев.

На основной окружности a b => 0 и cos a b => 1 , тогда

В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:

нулевые s = e = p * m / 2 , D = 0;

положительные s > e , => D > 0;

отрицательные s D D — коэффициент изменения толщины зуба (отношение приращения толщины зуба к модулю). Тогда толщину зуба по делительной окружности можно записать

Более подробно познакомиться с основными определениями и расчетными зависимостями можно в литературе [ 11.1 ] и в ГОСТ 16530-83.

Толщина зуба колеса по окружности произвольного радиуса .

Толщина зуба по дуге делительной окружности

Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 12.2

Подставляя в формулу угловой толщины эти зависимости, получим

Методы изготовления эвольвентных зубчатых колес .

Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода:

метод копирования, при котором рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности ( конгруентны ей, т. е. заполняют эту поверхность как отливка заполняет форму );

метод огибания, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения — резания и огибания (под огибанием понимается такое относительное движение заготовки и инструмента , которое соответствует станочному зацеплению , т. е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения).

Из вариантов изготовления по способу копирования можно отметить:

Нарезание зубчатого колеса профилированной дисковой или пальцевой фрезой (проекция режущих кромок которой соответствует конфигурации впадин). При этом методе резание производится в следующем прядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются пока не будут прорезаны все впадины. Производительность данного способа низкая, точность и качество поверхности невысокие.

Отливка зубчатого колеса в форму. При этом внутренняя поверхность литейной формы конгруентна наружной поверхности зубчатого колеса. Производительность и точность метода высокая, однако при этом нельзя получить высокой прочности и твердости зубьев.

Из вариантов изготовления по способу огибания наибольшее распространение имеют:

Обработка на зубофрезерных или зубодолбежных станках червячными фрезами или долбяками. Производительность достаточно высокая, точность изготовления и чистота поверхностей средняя. Можно обрабатывать колеса из материалов с невысокой твердостью поверхности.

Накатка зубьев с помощью специального профилированного инструмента. Обеспечивает высокую производительность и хорошую чистоту поверхности. Применяется для пластичных материалов, обычно на этапах черновой обработки. Недостаток метода образование наклепанного поверхностного слоя, который после окончания обработки изменяет свои размеры.

Обработка на зубошлифовальных станках дисковыми кругами. Применяемся как окончательная операция после зубонарезания (или накатки зубьев) и термической обработки. Обеспечивает высокую точность и чистоту поверхности. Применяется для материалов с высокой поверхностной прочностью.

Понятие о исходном, исходном производящем и производящем контурах .

Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются:

для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения — исходный контур;

для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения — исходный производящий контур.

По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими:

угол главного профиля a = 20 ° ;

коэффициент высоты зуба h * a = 1 ;

коэффициент высоты ножки h * f = 1.25 ;

коэффициент граничной высоты h * l = 2 ;

коэффициент радиуса кривизны переходной кривой r * f =с * /(1-sin a )= 0.38 ;

коэффициент радиального зазора в паре исходных контуров с * = 0.25.

Исходный производящий контур отличается от исходного высотой зуба h 0 = 2.5m.

Исходный и исходный производящий контуры образуют между собой конруентную пару (рис. 12.3), т.е. один заполняет другой как отливка заполняет заготовку (с радиальным зазором с * Ч m в зоне прямой вершин зуба исходной рейки). Принципиальное отличие этих контуров в том, что исходный контур положен в основу стандартизации зубчатых колес, а исходный производящий — в основу стандартизации зуборезного инструмента. Оба эти контура необходимо отличать от производящего контура — проекции режущих кромок инструмента на плоскость перпендикулярную оси заготовки.

Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4.

Линия станочного зацепления — геометрическое место точек контакта эвольвентной части профиля инструмента и эвольвентной части профиля зуба в неподвижной системе координат.

Смещение исходного производящего контура x*m — кратчайшее расстояние между делительной окружностью заготовки и делительной прямой исходного производящего контура.

Уравнительное смещение D y*m — условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора).

Окружность граничных точек r l — окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой.

Основные размеры зубчатого колеса .

Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).

Радиус окружности вершин

Радиус окружности впадин

Толщина зуба по делительной окружности.

Так как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать

Виды зубчатых колес (Классификация по величине смещения) .

В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением.

Подрезание и заострение зубчатого колеса .

Если при нарезании зубчатого колеса увеличивать смещение, то основная и делительная окружность не изменяют своего размера, а окружности вершин и впадин увеличиваются. При этом участок эвольвенты, который используется для профиля зуба, увеличивает свой радиус кривизны и профильный угол. Толщина зуба по делительной окружности увеличивается , а по окружности вершин уменьшается.

На рис. 12.7 изображены два эвольвентных зуба для которых

Для термобработанных зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба является нежелательным. Термообработка зубьев (азотирова-ние, цементация, цианирование), обеспечивающая высо Рис. 12.7 кую поверхностную прочность и твердость зубьев при сохранении вязкой серцевины, осуществляется за счет насыщения поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса, насыщаются углеродом больше. Поэтому после закалки они становятся более твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин зубьев меньших некоторых допустимых значений. То есть заостренным считается зуб у которого

При этом удобнее пользоваться относительными величинами [s a /m ]. Обычно принимают следующие допустимые значения

улучшение, нормализация [s a /m ] = 0.2;

цианирование, азотирование [s a /m ] = 0.25. 0.3;

цементация [s a /m ] = 0.35. 0.4.

Подрезание эвольвентных зубьев в станочном зацеплении

В процессе формирования эвольвентного зуба по способу огибания, в зависимости от взаимного расположения инструмента и заготовки возможно срезание эвольвентной части профиля зуба той частью профиля инструмента, которая формирует переходную кривую. Условие при котором это возможно определяется из схемы станочного зацепления. Участок линии зацепления, соответствующий эвольвентному зацеплению определяется отрезком B 1 . где точка B l определяется пересечением линии станочного зацепления и прямой граничных точек инструмента. Если точка B l располагается ниже (см. рис.12.8) точки N , то возникает подрезание зуба. Условие при котором нет подрезания можно записать так

Видео:Длина окружности. Математика 6 класс.Скачать

Диаметр основной окружности зубчатого колеса

где m y = p y / p = d y / z – модуль зацепления по окружности произвольного радиуса.

Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p . В зависимости от окружности по которой определен модуль различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) – число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого модуль можно определить как число милиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по окружности называемой делительной. Точнее делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба). Угловой шаг t – центральный угол соответствующий дуге p – окружному шагу по делительной окружности.

Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины – строчными буквами латинского алфавита, угловые – греческими буками; установлены индексы для величин :

по окружностям: делительной – без индекса, вершин – a , впадин – f , основная – b , начальная – w , нижних точек активных профилей колес – p , граничных точек – l ;

по сечениям: нормальное сечение – n , торцевое сечение – t , осевое сечение – x ;

относящихся к зуборезному инструменту – 0 .

Для параметров зубчатого колеса справедливы следующие соотношения

– диаметр окружности произвольного радиуса,

– диаметр делительной окружности,

– шаг по окружности произвольного радиуса,

– шаг по делительной окружности,

где a – угол профиля на делительной окружности,

a y – угол профиля на окружности произвольного радиуса.

Углом профиля называется острый угол между касательной к профилю в данной точки и радиусом – вектором, проведенным в данную точку из центра колеса.

Шаг колеса делится на толщину зуба s y и ширину впадины e y . Толщина зуба s y – расстояние по дуге окружности r y между разноименными точками профилей зуба. Ширина впадины e y – расстояние по дуге окружности r y между разноименными точками профилей соседних зубьев.

На основной окружности a b => 0 и cos a b => 1 , тогда

нулевые s = e = p * m / 2 , D = 0;

положительные s > e , => D > 0;

отрицательные s D D – коэффициент изменения толщины зуба (отношение приращения толщины зуба к модулю). Тогда толщину зуба по делительной окружности можно записать

Толщина зуба колеса по окружности произвольного радиуса .

Толщина зуба по дуге делительной окружности

Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 12.2

Подставляя в формулу угловой толщины эти зависимости, получим

Методы изготовления эвольвентных зубчатых колес .

метод огибания, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения – резания и огибания (под огибанием понимается такое относительное движение заготовки и инструмента , которое соответствует станочному зацеплению , т. е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения).

Из вариантов изготовления по способу копирования можно отметить:

Из вариантов изготовления по способу огибания наибольшее распространение имеют:

Понятие о исходном, исходном производящем и производящем контурах .

для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения – исходный контур;

для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения – исходный производящий контур.

По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими:

угол главного профиля a = 20 ° ;

коэффициент высоты зуба h * a = 1 ;

коэффициент высоты ножки h * f = 1.25 ;

коэффициент граничной высоты h * l = 2 ;

коэффициент радиуса кривизны переходной кривой r * f =с * /(1-sin a )= 0.38 ;

коэффициент радиального зазора в паре исходных контуров с * = 0.25.

Исходный производящий контур отличается от исходного высотой зуба h 0 = 2.5m.

Исходный и исходный производящий контуры образуют между собой конруентную пару (рис. 12.3), т.е. один заполняет другой как отливка заполняет заготовку (с радиальным зазором с * Ч m в зоне прямой вершин зуба исходной рейки). Принципиальное отличие этих контуров в том, что исходный контур положен в основу стандартизации зубчатых колес, а исходный производящий – в основу стандартизации зуборезного инструмента. Оба эти контура необходимо отличать от производящего контура – проекции режущих кромок инструмента на плоскость перпендикулярную оси заготовки.

Линия станочного зацепления – геометрическое место точек контакта эвольвентной части профиля инструмента и эвольвентной части профиля зуба в неподвижной системе координат.

Смещение исходного производящего контура x*m – кратчайшее расстояние между делительной окружностью заготовки и делительной прямой исходного производящего контура.

Уравнительное смещение D y*m – условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора).

Окружность граничных точек r l – окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой.

Основные размеры зубчатого колеса .

Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).

Радиус окружности вершин

Радиус окружности впадин

Толщина зуба по делительной окружности.

Виды зубчатых колес (Классификация по величине смещения) .

Подрезание и заострение зубчатого колеса .

На рис. 12.7 изображены два эвольвентных зуба для которых

улучшение, нормализация [s a /m ] = 0.2;

цианирование, азотирование [s a /m ] = 0.25. 0.3;

цементация [s a /m ] = 0.35. 0.4.

Подрезание эвольвентных зубьев в станочном зацеплении

– сверху – окружностью вершин диаметром d_a – формула (10.9);

– снизу – окружностью впадин диаметром d_f – формула (10.10);

– посередине профиля зуба – осью симметрии;

– переход от эвольвенты к окружности впадин осуществляют дугой переходной окружности радиусом = 0,4m.

Для определения положения оси симметрии зуба вычерчивают делительную окружность диаметром d – формула (10.6) – и по ней откладывают половину делительной толщины зуба

Полученную засечку соединяют с центром О окружностей, получая ось симметрии зуба. Вторую половину профиля получают, вычерчивая симметричный полупрофиль. Для повышения точности эвольвенты вводят дополнительную окружность произвольного радиуса r_y приблизительно посередине между окружностями вершин и делительной, на которой измеряют и откладывают толщину s_y. Профиль ножки зуба между эвольвентой и окружностью впадин формируется переходной кривой. Ширина впадины между зубьями по делительной окружности:

. (10.25)

Пример 10.1. Вычертить в масштабе эвольвенту и профиль одного зуба. Рассчитать d, d_b, d_a, d_f, p, s, e. Угол профиля a = 20 0 . Коэффициент высоты головки зуба = 1. Коэффициент радиального зазора c* = 0,25. Коэффициент радиуса переходной кривой = 0,4. Исходные данные: модуль m = 6 мм; число зубьев колеса z = 12; коэффициент смещения x = + 0,5; коэффициент уравнительного смещения Δy = 0,07.

Делительный диаметр d = 6∙12 = 72 мм.

Основной диаметр d_b = 6∙12∙cos20 ˚ = 67,66 мм.

Диаметр окружности вершин d_a = 6∙(12 + 2 + 2∙0,5 – 2∙0,07) = 89,16 мм.

Диаметр окружности впадин d_f = 6∙(12 – 2,5 + 2∙0,5) = 63 мм.

Делительная толщина зуба s = 0,5∙π∙6 + 2∙0,5∙6∙tg20 ˚ = 11,61 мм.

Шаг зубчатого колеса p = π∙ m = π∙6 = 18,85 мм.

Делительная ширина впадины e = 18,85 – 11,61 = 7,24 мм.

Радиус переходной кривой = 0,4∙6 = 2,4 мм.

Выполняем построения в соответствии с вышеизложенными рекомендациями в масштабе. Графическое решение задачи представлено на рис. 10.11.

Б) Геометрия нулевого зубчатого колеса.

Исходные данные для расчёта геометрии содержат модуль m и число зубьев z, а также параметры нормального исходного контура: α = 20º; ; с * = 0,25. Рассчитывают следующие геометрические параметры: делительный диаметр d – формула (10.6), основной диаметр d_в – формула (10.8), диаметр окружности вершин при отсутствии смещения:

диаметр окружности впадин:

шаг колеса – формула (10.2), делительная толщина зуба – формула (10.1), высота головки зуба, ножки зуба, полная высота зуба:

Геометрические параметры зубчатого колеса показаны на рис. 10.11.

В) Геометрия нулевого равносмещенного зацепления.

В равносмещенном зацеплении число зубьев шестерни z₁ 6 7 8

АлтГТУ 419
АлтГУ 113
АмПГУ 296
АГТУ 266
БИТТУ 794
БГТУ «Военмех» 1191
БГМУ 172
БГТУ 602
БГУ 153
БГУИР 391
БелГУТ 4908
БГЭУ 962
БНТУ 1070
БТЭУ ПК 689
БрГУ 179
ВНТУ 119
ВГУЭС 426
ВлГУ 645
ВМедА 611
ВолгГТУ 235
ВНУ им. Даля 166
ВЗФЭИ 245
ВятГСХА 101
ВятГГУ 139
ВятГУ 559
ГГДСК 171
ГомГМК 501
ГГМУ 1967
ГГТУ им. Сухого 4467
ГГУ им. Скорины 1590
ГМА им. Макарова 300
ДГПУ 159
ДальГАУ 279
ДВГГУ 134
ДВГМУ 409
ДВГТУ 936
ДВГУПС 305
ДВФУ 949
ДонГТУ 497
ДИТМ МНТУ 109
ИвГМА 488
ИГХТУ 130
ИжГТУ 143
КемГППК 171
КемГУ 507
КГМТУ 269
КировАТ 147
КГКСЭП 407
КГТА им. Дегтярева 174
КнАГТУ 2909
КрасГАУ 370
КрасГМУ 630
КГПУ им. Астафьева 133
КГТУ (СФУ) 567
КГТЭИ (СФУ) 112
КПК №2 177
КубГТУ 139
КубГУ 107
КузГПА 182
КузГТУ 789
МГТУ им. Носова 367
МГЭУ им. Сахарова 232
МГЭК 249
МГПУ 165
МАИ 144
МАДИ 151
МГИУ 1179
МГОУ 121
МГСУ 330
МГУ 273
МГУКИ 101
МГУПИ 225
МГУПС (МИИТ) 636
МГУТУ 122
МТУСИ 179
ХАИ 656
ТПУ 454
НИУ МЭИ 641
НМСУ «Горный» 1701
ХПИ 1534
НТУУ «КПИ» 212
НУК им. Макарова 542
НВ 777
НГАВТ 362
НГАУ 411
НГАСУ 817
НГМУ 665
НГПУ 214
НГТУ 4610
НГУ 1992
НГУЭУ 499
НИИ 201
ОмГТУ 301
ОмГУПС 230
СПбПК №4 115
ПГУПС 2489
ПГПУ им. Короленко 296
ПНТУ им. Кондратюка 119
РАНХиГС 186
РОАТ МИИТ 608
РТА 243
РГГМУ 118
РГПУ им. Герцена 124
РГППУ 142
РГСУ 162
«МАТИ» — РГТУ 121
РГУНиГ 260
РЭУ им. Плеханова 122
РГАТУ им. Соловьёва 219
РязГМУ 125
РГРТУ 666
СамГТУ 130
СПбГАСУ 318
ИНЖЭКОН 328
СПбГИПСР 136
СПбГЛТУ им. Кирова 227
СПбГМТУ 143
СПбГПМУ 147
СПбГПУ 1598
СПбГТИ (ТУ) 292
СПбГТУРП 235
СПбГУ 582
ГУАП 524
СПбГУНиПТ 291
СПбГУПТД 438
СПбГУСЭ 226
СПбГУТ 193
СПГУТД 151
СПбГУЭФ 145
СПбГЭТУ «ЛЭТИ» 380
ПИМаш 247
НИУ ИТМО 531
СГТУ им. Гагарина 114
СахГУ 278
СЗТУ 484
СибАГС 249
СибГАУ 462
СибГИУ 1655
СибГТУ 946
СГУПС 1513
СибГУТИ 2083
СибУПК 377
СФУ 2423
СНАУ 567
СумГУ 768
ТРТУ 149
ТОГУ 551
ТГЭУ 325
ТГУ (Томск) 276
ТГПУ 181
ТулГУ 553
УкрГАЖТ 234
УлГТУ 536
УИПКПРО 123
УрГПУ 195
УГТУ-УПИ 758
УГНТУ 570
УГТУ 134
ХГАЭП 138
ХГАФК 110
ХНАГХ 407
ХНУВД 512
ХНУ им. Каразина 305
ХНУРЭ 324
ХНЭУ 495
ЦПУ 157
ЧитГУ 220
ЮУрГУ 306

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Профиль боковых сторон зубьев зубчатых колес с эвольвентным зацеплением представляет собой две симметрично расположенные эвольвенты.

Эвольвента – это плоская кривая с переменным радиусом кривизны, образованная некоторой точкой на прямой, обкатывающейся без скольжения по окружности, диаметром (радиусом) d_b(r_b) называемой основной окружностью.

Основные параметры эвольвентного зацепления. На рис. 1.1 показано зацепление двух зубчатых колес с эвольвентным профилем. Рассмотрим основные параметры зацепления, их определения и стандартные обозначения.

В отличие от принятого ранее, обозначение всех параметров производится строчными, а не заглавными буквами с индексами, указывающими их принадлежность колесу, инструменту, типу окружности и виду сечения.

Стандартом предусмотрены три группы индексов:

первая группа: n, t, x – означает вид сечения, соответственно нормальный, торцовый (окружной), осевой;

вторая группа: a,f,b,w,y- означает, что параметр относится соответственно к окружностям выступов, впадин, основной, начальной и любой концентричной окружности. Для делительной окружности индекс не указывается;

третья группа: 1, 2, 0 – означает, что параметр относится соответственно к шестерне, колесу, зуборезному инструменту.

Порядок использования индексов определяется номером группы, т.е. вначале предпочтение отдается индексам первой группы, затем второй и т.д.

Некоторые индексы разрешается опускать в случаях, исключающих возникновение недоразумений или не имеющих применения по определению. Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.

Рассмотрим зацепление двух прямозубых цилиндрических (рис. 1.1) колес: с меньшим числом зубьев (z₁), называемого шестерней, и с большим числом зубьев (z₂), называемого колесом; соответственно с центрами колес в точках О₁ и О₂. В процессе обката шестерни с колесом происходит качение без скольжения двух центроид – окружностей, соприкасающихся в полюсе зацепления – Р. Эти окружности называются начальными, а их диаметры (радиусы) обозначаются с индексом w: d_wl (r_wl), d_w2 (r_w2). Для некорригированных колес эти окружности совпадают с делительными окружностями, обозначение диаметров (радиусов) которых дается без индексов первой и второй групп, т.е. для шестерни – d₁(r₁), для колеса – d₂(r₂).

Рис. 1.1. Эвольвентное зацепление зубчатых колес

Делительная окружность – окружность, на которой шаг между зубьями и угол профиля равны им же на делительной прямой зубчатой рейки, сцепленной с колесом. При этом шаг (Р = π · m) – расстояние между двумя соседними одноименными сторонами профиля. Отсюда диаметр делительной окружности колеса d = P · Z / π = m · Z

Модуль зуба (m = P / π) – величина условная, имеющая размерность в миллиметрах (мм) и используемая как масштаб для выражения многих параметров зубчатых колес. В зарубежной практике в этом качестве используется питч – величина, обратная модулю.

Основная окружность – это окружность, от которой образуется эвольвента. Все параметры, относящиеся к ней, обозначаются с индексом b например, диаметры (радиусы) колес в зацеплении: d_b1 (r_bl), d_b2 (r_b).

Касательно к основным окружностям через полюс зацепления Р проходит прямая N-N, а ее участок N₁-N₂ называется линией зацепления, по которой в процессе обката перемещается точка контакта сопрягаемых профилей колес. N₁-N₂ называется номинальной (теоретической) линией зацепления, обозначаемой буквой g. Расстояние между точками пересечения ее с окружностями выступов колес называется рабочим участком линии зацепления и обозначается g_a.

В процессе обката зубчатых колес точка контакта профилей перемещается в пределах активного (рабочего) участка линии зацепления g_a, которая является нормалью к профилям обоих колес в этих точках и одновременно общей касательной к обеим основным окружностям.

Угол между линией зацепления и перпендикуляром к линии, соединяющей центры сопрягаемых колес, называется углом зацепления. У корригированных колес этот угол обозначается α_w12; для некорригированных колес α_w12 = α .

Межцентровое расстояние некорригированных колес

Окружности выступов и впадин – окружности, проходящие соответственно через вершины и впадины зубьев колес. Их диаметры (радиусы) обозначаются: d_a1 ( r_a1 ), d_f1 ( r_f1 ), d_a2 ( r_a2 ), d_f2( r_f2 ).

Шаги зубьев колес – P_t Р_b, Р_n, Р_х – это расстояния между одноименными сторонами профиля, замеренные:

по дуге делительной окружности в торцовом сечении – окружной (торцевый) шаг P_t = d / Z;

по дуге основной окружности – основной шаг P_b = d_b / Z;

по контактной нормали (линии зацепления) – основной нормальный шаг Р_bn;

по нормали к направлению зубьев и по оси (у винтовых передач) – нормальный шаг Р_n и осевой шаг Р_х.

Коэффициент перекрытия, ε – отношение активной (рабочей) части линии зацепления к основному нормальному шагу:

Окружная (торцовая) толщина зуба, S_t – длина дуги делительной окружности, заключенная между двумя сторонами зуба.

Окружная ширина впадины между зубьями, е – расстояние между разноименными сторонами профиля по дуге делительной окружности.

Высота головки зуба, h_a – расстояние между окружностями выступов и делительной:

Высота ножки зуба h_f – расстояние между окружностями делительной и впадин:

Рабочий участок профиля зуба – геометрическое место точек контакта профилей сопрягаемых колес, определяется как расстояние от вершины зуба до точки начала эвольвенты. Ниже последней следует переходная кривая.

Переходная кривая профиля зуба – часть профиля от начала эвольвенты, т.е. от основной окружности до окружности впадин. При методе копирования соответствует форме головки зуба инструмента, а при методе обкатки образуется вершинной кромкой режущего инструмента и имеет форму удлиненной эвольвенты (для инструментов реечного типа) или эпициклоиды (для инструментов типа колеса).

Рис. 1.2. Зацепление зубчатой рейки с колесом

Понятие об исходном контуре рейки

Как было показано выше, частным случаем эвольвенты при z = (бесконечность) является прямая линия. Это дает основание использовать в эвольвентном зацеплении рейку с прямобочными зубьями. При этом любое зубчатое колесо данного модуля независимо от числа зубьев может быть сцеплено с рейкой того же модуля. Отсюда возникла идея обработки колес методом обкатки. В зацеплении колеса с рейкой (рис. 1.2) радиус начальной окружности последней равен бесконечности, а сама окружность превращается в начальную прямую рейки. Линия зацепления N₁N₂Так как профиль зубьев рейки – прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.4, а) проходит через полюс Р касательно к основной окружности колеса и перпендикулярно к боковой стороне профиля зуба рейки. В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α .

Так как профиль зубьев рейки – прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.3, а)

В соответствии со стандартами, принятыми в нашей стране для эвольвентного зацепления, исходный контур имеет следующие параметры зубьев в зависимости от модуля:

угол профиля α = 20°;

коэффициент высоты головки h * _a = 1;

коэффициент высоты ножки h * _f = 1,25;

коэффициент радиального зазора с * = 0,25 или 0,3;

коэффициент граничной (рабочей) высоты зуба h * _L = 2;

шаг зубьев Р = π · m;

толщина зуба S и ширина впадины е: S = е = 0,5Р = π · m / 2.

Делительная прямая рейки проходит по середине рабочей высоты зуба h_L.

Для зуборезных инструментов основные параметры зубьев по аналогии с изложенным выше задаются параметрами исходной инструментальной рейки (рис. 1.3, б). Так как зубья режущего инструмента обрабатывают впадину между зубьями колеса и могут нарезать колеса с модифицированным (фланкированным) профилем, между названными исходными контурами имеются существенные различия:

Высота головки зуба исходной инструментальной рейки h_a0 = (h * _f0 + с )m = 1,25 m, т.е. коэффициент высоты головки й h * _a0 =1,25. Высота ножки зуба h_f0 = 1,25 m, а полная высота зуба h = h_a0 + h_f0 = 2,5 m.

Если нарезаемое колесо имеет срез у головки (модифицированный профиль), то ножка зуба инструментальной рейки должна иметь утолщение с параметрами h _{ф 0} , α _{ф 0} , n _{ф 0}.

Толщина зуба у зубчатой рейки S = π · m / ₂ ,
а у инструментальной рейки при нарезании колес с модифицированным профилем зубьев S = π · m / ₂ ± ΔS

Рис. 1.3. Исходные контуры:

а – зубчатой рейки; б – инструментальной рейки

Поправка ΔS берется из справочников [23, 24] в зависимости от величины модуля зуба. Знак «+» берется для чистовых, а знак «-« – для черновых инструментов. В первом случае происходит утонение зубьев нарезаемого колеса с целью создания бокового зазора между зубьями сцепляемых колес, во втором случае утолщение, в результате чего нарезаемые зубья получают припуск на чистовую обработку.

У колес с обычным (модифицированным) профилем зубьев изменение толщины нарезаемых зубьев можно получить путем смещения инструментальной рейки относительно центра колеса и утолщение ее зубьев у ножки не требуется.

Параметры зацепления корригированных зубчатых колес. Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.

Применительно к долбякам корригирование дает возможность получения задних углов на режущих кромках (см. ниже).

Из известных методов корригирования на практике наибольшее применение нашло высотное корригирование, которое осуществляется путем смещения профиля исходной инструментальной рейки относительно центра нарезаемого колеса. Такое смещение принято считать положительным, если рейка отводится от центра колеса, и отрицательным, когда она приближается к его центру (рис. 1.4).

Рис. 1.4. Схема высотного корригирования зубчатого колеса:

1 – положительное смещение; 2 – нулевое смещение; 3 – отрицательное смещение

Величина смещения оценивается произведением х_о · m, где х – коэффициент смещения

При положительном смещении высота головки зуба нарезаемого колеса h ‘ _a1 увеличивается на величину хот, а высота ножки h ‘ _f1 уменьшается на ту же величину. При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.

Так как при этом положение делительной и основной окружностей колеса постоянно и не зависит от величины смещения, то неизбежно изменение толщины зуба нарезаемого колеса по делительной окружности из-за смещения делительной прямой рейки относительно начального положения на величину ± х_о · m. Как видно из рис. 1.5, толщина зуба по делительной окружности у корригированного колеса при смещении рейки инструмента

Знак «+» берется при положительном, а знак «-« – при отрицательном смещении.

При расчетах зуборезных инструментов, например долбяков, зубья которых корригированы, возникает необходимость определения толщины зуба на окружности любого радиуса – r_у, концентричной с делительной окружностью радиусом r.