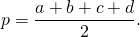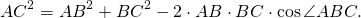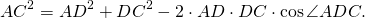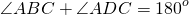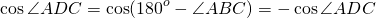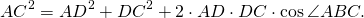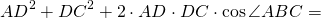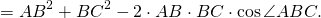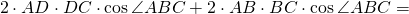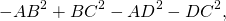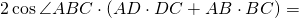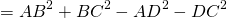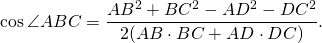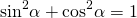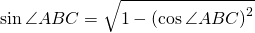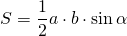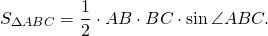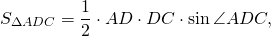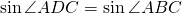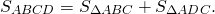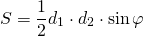Таблица 3 площадь четырехугольника о центр вписанной окружности найти

Формулы для площадей четырехугольников

Вывод формул для площадей четырехугольников

Вывод формулы Брахмагупты для площади вписанного четырехугольника

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

a – сторона,
h_a – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

a – сторона,
h_a – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

,

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab
Параллелограмм
Квадрат		S = a 2
		S = 4r 2
Ромб
Трапеция
		S = m h
Дельтоид		S = ab sin φ
Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

,

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник
Параллелограмм
Квадрат
	S = a 2 где a – сторона квадрата
	S = 4r 2
Ромб
Трапеция
Дельтоид
	где a и b – неравные стороны, φ1 – угол между сторонами, равными a , φ2 – угол между сторонами, равными b .
Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

Прямоугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

,

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

,

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

,

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

Площадь вписанного четырехугольника

Как найти площадь вписанного четырехугольника?

I способ.

Площадь вписанного четырёхугольника может быть найдена по формуле Брахмагупты:

где p — полупериметр четырёхугольника, то есть

(формулу Герона можно рассматривать как частный случай этой формулы при d=0).

Площадь четырёхугольника ABCD, вписанного в окружность, можно найти как сумму площадей треугольников, например, ABC и ADC.

Из треугольника ABC по теореме косинусов

Аналогично, из треугольника ADC

Так как четырехугольник ABCD вписан в окружность,

Приравниваем правы части равенств для AC²

Найдём синус этого угла, используя основное тригонометрическое тождество

(так как их сумма равна 180º, а sin(180º-α )=sinα).

В частных случаях: если в окружность вписан правильный четырёхугольник (то есть квадрат), прямоугольник либо четырёхугольник, диагонали которого взаимно перпендикулярны — решение задачи может быть упрощено.

Площадь любого четырёхугольника, в том числе, и вписанного, равна половине произведения его диагоналей на синус угла между ними:

В следующий раз рассмотрим конкретные примеры нахождения площади вписанного четырёхугольника.

Калькулятор расчета площади четырехугольника

В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через диагонали и угол между ними

Формула расчета

2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

Формула расчета

p – полупериметр четырехугольника, равняется:

🌟 Видео