Через точку a к данной окружности проведены касательная ab (3 видео)

Через точку А проведены касательная АВ ( В — точка касания) и секущая, пересекающая окружность в точках С и Е так, что АВ = 10 см, АЕ = 20 см?

Геометрия | 5 — 9 классы

Через точку А проведены касательная АВ ( В — точка касания) и секущая, пересекающая окружность в точках С и Е так, что АВ = 10 см, АЕ = 20 см.

Найдите длину АС.

Вспоминаем теорему о касательной и секущей :

Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.

АС обозначаем за Х, ну и решаем :

Как «Лучшее решение» не забудь отметить, ОК.

Содержание

Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекает окружность в точках Е и F?
Через точку A проведены касательная AB (B — точка касания) и секущая, пересекающая окружность в точках C и K так, что AC = 4 см, AK = 16 см?
Из одной точки к окружности проведены касательная и секущая?
К окружности с центром в точке О проведены касательная АВ(В — точка касания) и секущая АО?
Из точки Е к окружности проведены касательная АЕ и секущая ВЕ?
Через точку A проведены касательная AB (B — точка касания) и секущая, пересекающая окружность в точках C и K так, что AC = 4 см, AK = 16 см?
Через точку А проведена касательная АВ ( В — точка касания) и секущая , которая пересекает окружность в точках С и Д?
Через точку A проведены касательная AB (B — точка касания) и секущая, пересекающая окружность в точках C и K так, что AC = 4 см, AK = 16 см?
СРОЧНОО?
К окружности с центром в точке О проведены касательная АВ(В — точка касания) и секущая АО?
Через точку a к данной окружности проведены касательная ab
Окружность. Касательная к окружности.
🔥 Видео

Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать

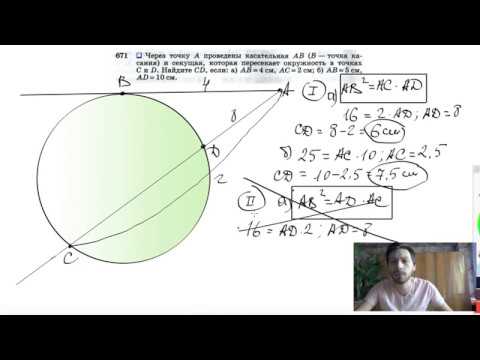
Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекает окружность в точках Е и F?

Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекает окружность в точках Е и F.

Найдите EF, если AB = 9, AF = 15.

Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать

Через точку A проведены касательная AB (B — точка касания) и секущая, пересекающая окружность в точках C и K так, что AC = 4 см, AK = 16 см?

Через точку A проведены касательная AB (B — точка касания) и секущая, пересекающая окружность в точках C и K так, что AC = 4 см, AK = 16 см.

Найдите длину AB Ответ : 8 см.

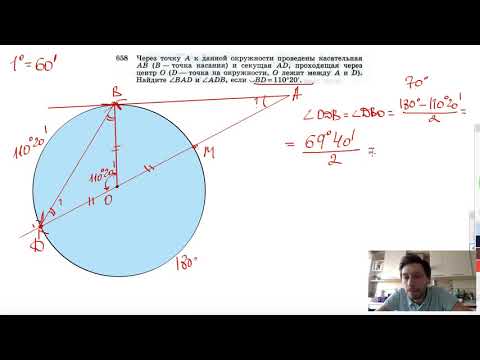
Видео:№658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая ADСкачать

Из одной точки к окружности проведены касательная и секущая?

Из одной точки к окружности проведены касательная и секущая.

Касательная длиннее внутренней и внешей секущей на2 и 4 см.

Найдите длину секущей.

Видео:Геометрия Докажите, что если через точку A к окружности проведены касательная AM (M – точка касания)Скачать

К окружности с центром в точке О проведены касательная АВ(В — точка касания) и секущая АО?

К окружности с центром в точке О проведены касательная АВ(В — точка касания) и секущая АО.

Найдите угол АОВ, если угол ОАВ = 19градусов.

Видео:На отрезке AB выбрана точка C так, что AC=75 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Из точки Е к окружности проведены касательная АЕ и секущая ВЕ?

Из точки Е к окружности проведены касательная АЕ и секущая ВЕ.

Эта секущая пересекает окружность в точках В и С.

Найдите длину АЕ, если ВС — 5см, ВЕ — 4см.

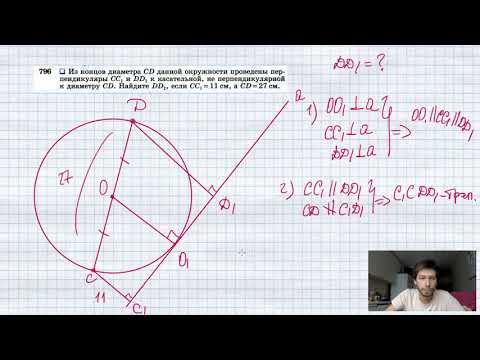
Видео:№796. Из концов диаметра CD данной окружности проведены перпендикуляры СС1 и DD1 к касательнойСкачать

Через точку A проведены касательная AB (B — точка касания) и секущая, пересекающая окружность в точках C и K так, что AC = 4 см, AK = 16 см?

Найдите длинну AB.

Видео:№645. Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательнойСкачать

Через точку А проведена касательная АВ ( В — точка касания) и секущая , которая пересекает окружность в точках С и Д?

Через точку А проведена касательная АВ ( В — точка касания) и секущая , которая пересекает окружность в точках С и Д.

Найти СД, если АВ = 5см АД = 10см.

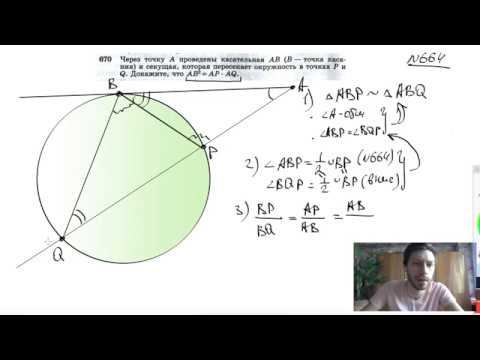
Видео:№670. Через точку А проведены касательные АВ (В — точка касания) и секущая, которая пересекаетСкачать

Через точку A проведены касательная AB (B — точка касания) и секущая, пересекающая окружность в точках C и K так, что AC = 4 см, AK = 16 см?

Найдите длину AB Ответ : 8 см.

Видео:№640. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательныеСкачать

СРОЧНОО?

К окружности радиуса 5 см из точки А проведена касательная АК с точкой касания К.

Длина АК равна см.

Найдите (см) расстояние от точки А до ближайшей точки окружности.

Видео:№ 180 - Геометрия 7-9 класс АтанасянСкачать

К окружности с центром в точке О проведены касательная АВ(В — точка касания) и секущая АО?

К окружности с центром в точке О проведены касательная АВ(В — точка касания) и секущая АО.

Найдите длину отрезка секущей АО, если AB = 40мм, OB = 30мм.

Перед вами страница с вопросом Через точку А проведены касательная АВ ( В — точка касания) и секущая, пересекающая окружность в точках С и Е так, что АВ = 10 см, АЕ = 20 см?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Трапеция, ее признаки и свойства Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами. . Средняя линия трапеции — отрезок..

Решение в приложении.

Мама за 30 минут прошла 2, 5 км, Юра проехал 6 км. Имеем прямоугольный треугольник с катетами 2, 5 и 6 км. Надо найти гипотенузу. С² = 2, 5² + 6² = 6, 25 + 36 = 72, 25 с = √72, 25 = 8, 5 Ответ : 8, 5 км.

Вот 180 — (65 + 50) = 65 и т. Д На фото.

По — моему, есть ошибка в вопросе.

Пусть х — один из смежных углов, тогда второй угол 180 — х. Биссектриса первого угла — х / 2, второго — (180 — х) / 2 = 90 — (x / 2). Т. к. Биссектрисы выходят из одной точки то угол между ними равен (х / 2) + 90 — (х — 2) = 90. Следовательно, би..

126 градусов, 76 + 50 = 126.

АОВ + ВОР = 76 + 50 = 126 поплидмзмшь.

Розв»язок додала. Вiдповiдь 112см².

10 : 2 = 5 25 : 2 = 12, 5 5 ^ 2 + 12, 5 ^ 2 = 13, 462 ^ 2 13, 462 * 4 = 53, 848.

Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Через точку a к данной окружности проведены касательная ab

Решение:
пусть О — центр окружности
пусть АВ = а
пусть АР = в
пусть AQ = c
пусть АO = х
пусть ОВ = ОР = ОQ = r
пусть угол РАО = у
**************************
по теореме Пифагора и по теореме косинусов выразим стороны трех треугольников с общей вершиной А и общей стороной АО
получим 3 уравнения
x² = a² + r²
r²=x² + b²-2xb*cos(y)
r²=x²+c²-2xc*cos(y)
***************
x² = a² + r²
r²=a² + r²+ b²-2xb*cos(y)
r²=a² + r²+c²-2xc*cos(y)
***************
a² + b²=2xb*cos(y)
a² +c²=2xc*cos(y)
***************
(a² + b²)*c=2xbc*cos(y)
(a² +c²)*b=2xbc*cos(y)
***************
(a² +c²)*b=(a² + b²)*c
***************
a²b +c²*b=a²c + b²*c
***************
a²b — a²c = b²*c-c²*b
***************
a²(b — c) = bc(b-c)
***************
a² = bc
***************
AB²= AP*AQ — что и требовалось доказать

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Окружность. Касательная к окружности.

Прямая (MN), имеющая с окружностью только одну общую точку (A), называется касательной к окружности.

Общая точка называется в этом случае точкой касания.

Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.

Теорема.

Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.

Пусть O — центр некоторого круга и OA какой-нибудь его радиус. Через его конец A проведем MN ⊥ OA.Требуется доказать, что прямая MN — касательная, т.е. что эта прямая имеет с окружностью только одну общую точку A.

Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B. Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.

Но этого быть не может, так как, если OA — перпендикуляр, то OB должна быть наклонной к MN, а наклонная больше перпендикуляра.

Обратная теорема.

Если прямая касательная к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.

Следствие.

Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.

Теорема.

Касательная параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.

Пусть прямая AB касается окружности в точке M и параллельна хорде СD. Требуется доказать, что ∪CM= ∪MD.

Проведя через точку касания диаметр ME, получаем: EM ⊥ AB и следовательно, EM ⊥ СD. Поэтому СM=MD.

Через данную точку провести касательную к данной окружности.

Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.

Рассмотрим тот случай, когда точка дана вне круга.

Пусть требуется провести к окружности с центром O касательную через точку A. Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.

Проведя затем хорды OB и OС, соединим точку A с точками D и E, в которых эти хорды пересекаются с данной окружностью. Прямые AD и AE — касательные к окружности O. Действительно, из построения видно, что треугольники AOB и AOС равнобедренные (AO = AB =AС) с основаниями OB и OС, равными диаметру круга O.

Так как OD и OE — радиусы, то D — середина OB, а E — середина OС, значит AD и AE — медианы, проведенные к основаниям равнобедренных треугольников, и потому перпендикулярны к этим основаниям. Если же прямые DA и EA перпендикулярны к радиусам OD и OE, то они — касательные.

Следствие.

Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.

Так AD=AE и ∠OAD = ∠OAE потому, что прямоугольные треугольники AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны. Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.