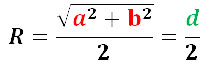С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
- Вписать прямоугольник в окружность формула
- Прямоугольник. Онлайн калькулятор
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
- Радиус описанной окружности прямоугольника
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
- Расчет длины стороны
Видео:Длина окружности. Математика 6 класс.Скачать
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
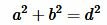 . | (1) |
Из равенства (1) найдем d:
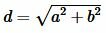 . | (2) |
Пример 1. Стороны прямоугольника равны 
. Найти диагональ прямоугольника.
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:
 |
Ответ: 
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Видео:Длина окружности. Площадь круга - математика 6 классСкачать
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac<large sqrt> ) | (4) |
Пример 2. Стороны прямоугольника равны 
. Найти радиус окружности, описанной вокруг прямоугольника.
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:
 |
 |
Ответ: 
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
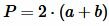 | (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:
 |
Ответ: 
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
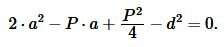 | (10) |
Вычислим дискриминант квадратного уравнения (10):
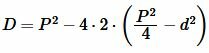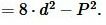  | (11) |
Сторона прямоугольника вычисляется из следующих формул:
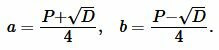 | (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна 
, а периметр равен 
. Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):
 |
Подставляя значения и 
в первую формулу (12), получим:
 |
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и 
в формулу, получим:
 |
Ответ: 
, 
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать
Вписать прямоугольник в окружность формула
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
|
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Видео:Длина дуги окружности. 9 класс.Скачать
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Видео:№ 5.6. Периметр и площадь квадрата (дополнение)Скачать
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
|
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
|
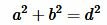| . | (1) |
Из равенства (1) найдем d:
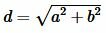| . | (2) |
Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:
|
Ответ:
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
|
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac ) | (4) |
Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:
|
|
Ответ:
Видео:Вписанный в окружность прямоугольный треугольник.Скачать
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
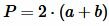| (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:
|
Ответ:
Видео:Окружность. Круг. 5 класс.Скачать
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
| (6) |
| (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
| (8) |
| (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
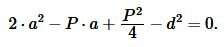| (10) |
Вычислим дискриминант квадратного уравнения (10):
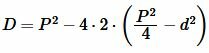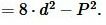| (11) |
Сторона прямоугольника вычисляется из следующих формул:
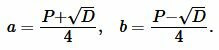| (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):
|
Подставляя значения и в первую формулу (12), получим:
|
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:
|
Ответ: ,
Видео:Углы, вписанные в окружность. 9 класс.Скачать
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Видео:Геометрия с нуля! / Выпуск № 6. Формула квадрата, вписанного в окружность / ОГЭ по математике 2022Скачать
Радиус описанной окружности прямоугольника
Как известно, прямоугольником является четырехугольник с прямыми углами. Противоположные углы прямоугольника в сумме составляют 180°, соответственно, вокруг него можно описать одну окружность, при этом, вершины прямоугольника должны быть расположены на этой окружности. Центр прямоугольника и описанной вокруг него окружности размещен в месте пересечения диагоналей. Диагонали прямоугольника равны. Если известны стороны прямоугольника, можно рассчитать величину диагоналей по теореме Пифагора. Диагональ прямоугольника является в то же время и диаметром описанной окружности. R описанной окружности представляет половину диагонали прямоугольника и рассчитывается путем извлечения квадратного корня из суммы квадратов его сторон деленный на 2 или как половина его диагонали:
d — диагональ;
a, b — величины сторон прямоугольника.
Если известны стороны прямоугольника или диагонали, можно быстро найти R описанной окружности с помощью калькулятора.
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать
Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать
Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).