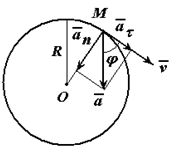
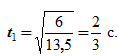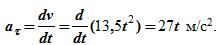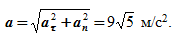Движение точки по окружности задано уравнением s 2t 3 (2 видео)

iSopromat.ru

Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.

Содержание

Задача
Решение
Движение точки по окружности задано уравнением s 2t 3
Движение точки по окружности задано уравнением s 2t 3
📹 Видео

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Задача

Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t 3 ( s в метрах, t в секундах).

Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t₁, когда скорость будет равна 6 м/с (рисунок 1.6).

Видео:Кинематика точки Движение по окружностиСкачать

Решение

Дифференцируя s по времени, находим модуль вектора скорости точки

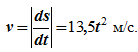
Подставляя в это выражение значение скорости, получим 6=13,5t₁ 2 , откуда находим

Касательное ускорение для любого момента времени равно

Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно

Модуль вектора полного ускорения точки равен

Угол между вектором полного ускорения и вектором скорости определим следующим образом:

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Движение точки по окружности задано уравнением s 2t 3

тангенциальное нормальное полное ускорения

Колесо с радиусом 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = 5+t+2t 2 +t 3 рад. Для точек, лежащих на ободе колеса, определить угловую скорость, угловое, нормальное, тангенциальное и полное ускорения к концу второй секунды. Какой угол образует вектор полного ускорения и вектор линейной скорости?

Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t 3 . Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

Колесо радиусом 0,3 м вращается согласно уравнению φ = 5–2t+0,3t 2 . Найти нормальное, тангенциальное и полное ускорение точек на ободе колеса через 5 с после начала движения.

Шарик массы т = 100 г, подвешенный на нити, отвели в сторону так, что нить образовала прямой угол с вертикалью, а затем отпустили. Найти: 1) тангенциальное, нормальное и полное ускорение и натяжение нити в зависимости от угла θ отклонения нити от вертикали; 2) натяжение нити в тот момент, когда вертикальная составляющая скорости шарика максимальна.

Используя данные предыдущей задачи, определить: 1) частоту вращения диска в момент времени t₂ в об/с и об/мин; 2) в момент времени t₂ определить скорость, нормальное, тангенциальное и полное ускорение точек, находящихся на расстоянии 10 см от оси вращения.
Данные из предыдущей задачи: t₂ = 15 с; ω(t₂) = 11,8 рад/с; β(t₂) = 1,1 рад/с 2 .
Предыдущая задача: Диск вращается согласно уравнению φ = а + bt + ct 2 + dt 3 , где φ — угол поворота радиуса в радианах, t — время в секундах. Определить угловую скорость и ускорение в моменты времени t₁ = 11 с и t₂ = 15 с. Каковы средние значения угловой скорости и углового ускорения в промежутке времени от t₁ = 11 до t₂ = 15 с включительно, если для Вашего варианта а = 1, b = 2 с –1 , с = 0,1 с –2 , d = 0,01 с –3 ?

Точка движется по кругу так, что зависимость пути от времени задается уравнением: S = А + Bt +Ct 2 , где В = –2 м/с и С = 1 м/с 2 . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 3 с после начала движения, если известно, что нормальное ускорение в момент времени 2 с составляет 0,5 м/с 2 .

Найти нормальное, тангенциальное и полное ускорение электрона на произвольной стационарной орбите в ионе Не+.

Движение точки по окружности радиуса R = 4 м задано уравнением: S = A+Bt+Ct 2 . Определить тангенциальное, нормальное и полное ускорение точки в момент времени t = 2 с, если А = 10 м, В = –2 м/с и С = 1 м/с 2 .

Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Длина пути автомобиля выражается уравнением S = 10+10t+0,5t 2 (путь — в метрах, время — в секундах). Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения через 5 с после начала движения.

Материальная точка движется по окружности радиуса 80 см по закону S = 10t–0,1t 3 (путь в метрах, время в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения через 2 с после начала движения.

Материальная точка движется по окружности диаметром 40 м. Зависимость ее координаты от времени движения определяется уравнением S = t 3 +4t 2 –3t+8. В какой момент точка изменяет направление движения? Определить пройденный путь, скорость, нормальное, тангенциальное и полное ускорение движущейся точки через 4 с после начала движения.

Тело движется по криволинейной траектории. Пройденный путь меняется со временем по закону s = 2 + 0,5t 2 , м. Определить нормальное, тангенциальное и полное ускорение при t = 1 с. Радиус кривизны траектории движения в этот момент времени равен 50 см. Какова средняя скорость за 1 с движения?

Материальная точка начала вращаться с постоянным угловым ускорением из положения 1 и через 0,1 с оказалась в положении 2. Найти угловые ускорение и скорость в точке 2. Указать направления тангенциального, нормального и полного ускорений, а также линейной и угловой скоростей для положения 2.

Движение точки по окружности радиусом R = 2 м задано уравнением φ = A+Bt+Ct 2 , где А = 10 м, В = –3 м/с, С = 2 м/с 2 . Найти тангенциальное, нормальное и полное ускорения точки в момент времени t = 2 с.

Видео:Физика 10 Равномерное движение точки по окружностиСкачать

Движение точки по окружности задано уравнением s 2t 3

Глава 7. Кинематика точки.

7.8. Ускорение точки при естественном способе задания движения.

7.8.1. Даны нормальное а_n = 2,5 м/с 2 и касательное а_τ = 1,5 м/с 2 ускорения точки. Определить полное ускорение точки. (Ответ 2,92)

7.8.2. Определить модуль ускорения точки, если его вектор а = 2,5n + 3,5τ, где n и τ — орты естественного триэдра. (Ответ 4,30)

7.8.3. Точка движется по криволинейной траектории с касательным ускорением а_τ = 1,4 м/с 2 . Определить нормальное ускорение точки в момент времени, когда ее полное ускорение а = 2,6 м/с 2 . (Ответ 2,19)

7.8.4. Определить нормальное ускорение точки в момент времени, когда ускорение точки а = 1,5 м/с 2 , а угол между векторами ускорения и скорости равен 65°. (Ответ 1,36)

7.8.5. Точка движется по окружности. Определить радиус окружности, если в момент времени, когда скорость v = 10 м/с, вектор ускорения и вектор скорости, равный по модулю 1,2 м/с, образуют угол 30°. (Ответ 167)

7.8.6. Дан график касательного ускорения а_τ = а_τ (t) движения точки по окружности радиуса 9 м. Определить полное ускорение в момент времени t = 2 с, если при t_o = 0 скорость точки v₀ = 0.
(Ответ 3,74)

7.8.7. Ускорение точки а = 1 м/с. Векторы ускорения и скорости образуют угол 45°. Определить скорость в км/ч, если радиус кривизны траектории ρ = 300 м. (Ответ 52,4)

7.8.8. Точка движется по окружности, радиус которой r = 200 м, с касательным ускорением 2 м/с 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени, когда ее скорость v = 10 м/с. (Ответ 14,0)

7.8.9. Точка движется по окружности, радиус которой r = 50 м, со скоростью v = 2t. Определить модуль полного ускорения в момент времени t = 5 с. (Ответ 2,83)

7.8.10. Задано уравнение движения точки по криволинейной траектории: s = 0,2t 2 + 0,3t. Определить полное ускорение точки в момент времени t = 3 с, если в этот момент радиус кривизны траектории ρ = 1,5 м. (Ответ 1,55)

7.8.11. Определить скорость точки в момент времени, когда радиус кривизны траектории ρ = 5 м, касательное ускорение а_τ = 2 м/с 2 , а tgβ = 3, где β — угол между векторами скорости и ускорения точки (Ответ 5,48)

7.8.12. Даны графики ускорения а_τ = а_τ(t) и а_n = a_n(t). Определить, какой угол в градусах образует полное ускорение с направлением скорости в момент времени t = 3 с. (Ответ 56,3)

7.8.13. По окружности радиуса r = 6 м движется точка со скоростью v = 3t. Определить угол в градусах между ускорением и скоростью точки в момент времени t = 1 с. (Ответ 26,6)

7.8.14. Точка движется по окружности радиуса r = 9 м. Определить скорость точки в момент времени, когда касательное ускорение а_τ = 2 м/с 2 , а вектор полного ускорения а образует угол 70 o c касательной к траектории. (Ответ 7,03)

7.8.15. Дан график скорости v = v(t) движения точки по окружности радиуса 8 м. Определить полное ускорение в момент времени t = 4 с. (Ответ 2,24)

7.8.16. Точка движется но окружности радиуса r = 200 м из состояния покоя с постоянным касательным ускорением а_τ = 1 м/с 2 . Определить полное ускорение точки в момент времени t = 20 с. (Ответ 2,24)

7.8.17. Точка движется по окружности радиуса r = 2 м. Нормальное ускорение точки меняется согласно закону а_n = 2t 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени t = 1 с. (Ответ 45)

7.8.18. Задан закон движении точки по траектории: s = 0,5t 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени t₁ = 3 с, когда радиус кривизны ρ = 4 м. (Ответ 66,0)

7.8.19. По окружности радиуса r = 1м движется точка согласно уравнению s = 0,1t 3 . Определить полное ускорение точки в момент времени t = 2 с. (Ответ 1,87)

7.8.20. Точка движется по криволинейной траектории с касательным ускорением а_τ = 2 м/с 2 . Определить угол в градусах между векторами скорости и полного ускорении точки в момент времени t = 2 с, когда радиус кривизны траектории ρ = 4м, если при t₀ = 0 скорость точки v₀ = 0. (Ответ 63,4)

Сборник коротких задач по теоретической механике.
Кепе О.Э.

Книга состоит из 1757 заданий которые предназначены для бысторого
контроля знаний на занятиях и зачетах а также для допуска к экзамену.
Задачи имеют ответы.

Издательство «Высшая школа» 1989 Москва

Также решение задач Кепе можно скачать здесь:
Мобильное приложение для Андроид: