- Определение
- Теорема
- Доказательство теоремы
- Определить возможность существования треугольника по сторонам
- Задача
- Решение
- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- 💥 Видео
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.
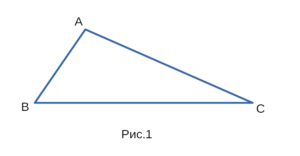
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
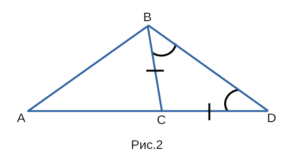
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы
- Проведем отрезок CD равный отрезку CB.
- △BCD — равнобедренный, значит ∠ CBD=∠CDB.
- Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Определить возможность существования треугольника по сторонам
Задача
Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.
Дано: a , b , c – стороны предполагаемого треугольника.
Требуется сравнить длину каждого отрезка-стороны с суммой двух других. Если хотя бы в одном случае отрезок окажется больше суммы двух других, то треугольника с такими сторонами не существует.
Решение
Ниже приведены решения задачи на языке программирования Паскаль двумя способами. В первом случае все стороны проверяются в одном операторе if; во втором случае каждое условие проверяется отдельно, а программа содержит вложенные операторы if-else.
Программа 1 (предпочтительный способ решения):
В языке Паскаль логический оператор and имеет приоритет над операторам >, if проверяется, что каждая из сторон меньше суммы других. Если хотя бы одна будет больше, то все логическое выражение вернет ложь ( false ). В таком случае сработает ветка else .
В данном случае существование треугольника проверяется по-этапно. Если первое условие возвращает ложь, то программа переходит к последнему else. Если же первое условие соблюдено, то поток выполнения программы оказывается у вложенного if. Здесь проверяется уже второе условие. Если оно возвращает ложь, то программа переходит к предпоследнему else. Если и второе логическое выражение возвращает истину (true), то программа идет к третьему условию. При его соблюдении выполняется тело самого вложенного оператора if. При его несоблюдении сработает самое вложенное else.
Несмотря на то, что данная программа кажется длиннее, в определенных ситуациях она может выполняться быстрее, чем первая. Здесь если внешнее if возвращает ложь, то остальные логические выражения вообще не проверяются. В первой программе могут и проверяться (это зависит от особенностей языка программирования).
Видео:Треугольники. 7 класс.Скачать

Треугольник. Формулы и свойства треугольников.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Первый признак равенства треугольников. 7 класс.Скачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Признаки равенства треугольников. 7 класс.Скачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Неравенства треугольника. 7 класс.Скачать

Связь между вписанной и описанной окружностями треугольника
Видео:Все про окружность для задания 16 на ОГЭ по математикеСкачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Аксиома существования треугольника, равного данномуСкачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
💥 Видео
Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Средняя линия. Теорема о средней линии треугольникаСкачать

Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать