Свойство углов при параллельных прямых 7 класс таблица 7

При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Углы, образующиеся при пересечении двух прямых третьей прямой

Рисунок	Определение углов
	Внутренние накрест лежащие углы
	Внешние накрест лежащие углы
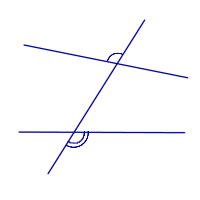	Соответственные углы
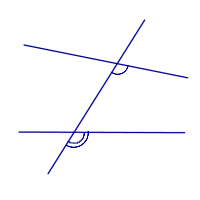	Внутренние односторонние углы
	Внешние односторонние углы

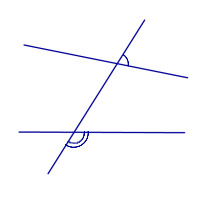Внутренние накрест лежащие углы

Внешние накрест лежащие углы

Соответственные углы

Внутренние односторонние углы

Внешние односторонние углы

Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.

Определение . Две прямые на плоскости называются параллельными, если они не имеют общих точек.

Замечание . Два отрезка называются параллельными , если они лежат на параллельных прямых.

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Признаки параллельности двух прямых

Рисунок	Признак параллельности
	Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны
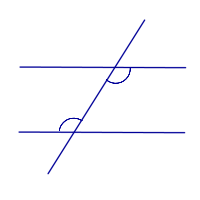	Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны
	Прямые параллельны тогда и только тогда, когда соответственные углы равны
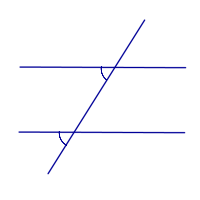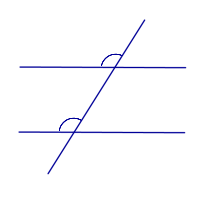	Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°
	Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Прямые параллельны тогда и только тогда,
когда внутренние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда внешние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда соответственные углы равны

Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Рисунок	Признак параллельности
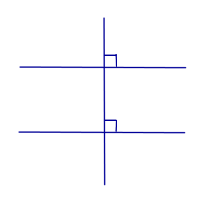	Две прямые, перпендикулярные к третьей прямой, параллельны

Две прямые, перпендикулярные к третьей прямой, параллельны

Переход свойства параллельности прямых

Рисунок	Признак параллельности
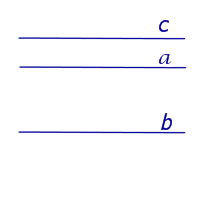	Если прямая a параллельна прямой b , а прямая b параллельна прямой c , то прямая a параллельна прямой c

Если прямая a параллельна прямой b ,
а прямая b параллельна прямой c ,
то прямая a параллельна прямой c

Задача . Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.

Решение . Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Урок-практикум по геометрии в 7-м классе «Свойства углов, образованных при пересечении параллельных прямых секущей»

Разделы: Математика

Цели урока: (Слайд №1)
Образовательные: закрепление умений использовать знания признаков, свойств углов, образованных при пересечении параллельных прямых секущей, научить видеть различные способы при решении одной задачи.
Воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения.
Развивающие: развитие логического мышления учащихся, внимания, активности, чувство ответственности, самостоятельности, культуры общения.
Тип урока: урок обобщения и систематизации знаний учащихся.
Организационные формы: парная, дифференцированно групповая.
Технология: уровневая дифференциация.
Структура урока:

• вводное слово учителя
• самостоятельная работа групп №2, №3
• актуализация знаний учащихся группы №1
  1. диктант
  2. тест
• самостоятельная работа группы №1
• защита у доски работ группами №2, №3

К данному уроку прилагается презентация (Приложение 1)

Ход урока:
Вводное слово учителя
Многие великие люди всех времен и народов говорили о значении математики. Не только ученые — математики, но и поэты, писатели, философы. Высказывание одного великого мыслителя: «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» Леонардо да Винчи (слайд №2).
Предметом исследования нашего урока будут углы, образованные при пересечении параллельных прямых секущей. Задачей нашего урока является обобщение и систематизация ваших знаний по данной теме.
В ходе групповой, парной, самопроверки вы еще раз закрепите знания свойств углов, образованных при пересечении параллельных прямых секущей (слайд №3).

Организация работы групп

• класс делится на 3 группы по уровню их обученности
• каждая группа получает определенные задания

1. группа №3 — уровень «4-5». Решают по 3 задачи с последующей защитой у доски.
   Выполняют в тетрадях и сдают учителю.

   Задания для групп с уровнем обученности «4-5»

   Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

   

   Признаки и свойства параллельных прямых

   Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

   

   Признаки параллельных прямых

   1. Если две прямые параллельны третьей прямой, то они являются параллельными:

   

   2. Если две прямые перпендикулярны третьей прямой, то они параллельны:

   

   Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.

   3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:

   

   Если ∠1 + ∠2 = 180°, то a || b.

   4. Если соответственные углы равны, то прямые параллельны:

   

   5. Если внутренние накрест лежащие углы равны, то прямые параллельны:

   

   Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

   

   Свойства параллельных прямых

   Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.

   1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:

   

   Если a || b, то ∠1 + ∠2 = 180°.

   2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:

   

   3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:

   

   Следующее свойство является частным случаем для каждого предыдущего:

   4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

   

   Пятое свойство — это аксиома параллельности прямых:

   5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:

   🔥 Видео

   Свойства параллельных прямых - 7 класс геометрияСкачать

   

   МЕРЗЛЯК 7 ГЕОМЕТРИЯ. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. ПАРАГРАФ-15Скачать

   

   7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

   

   Параллельные прямые (задачи).Скачать

   

   7 класс. Геометрия. Параллельность прямых. Признаки и свойства. Углы при пересечении прямых. Урок #7Скачать

   

   №201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать

   

   СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. §15 геометрия 7 классСкачать

   

   Урок 15 Свойства параллельных прямых (7 класс)Скачать

   

   Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

   

   ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ решение задач 7 класс геометрия АтанасянСкачать

   

   7 класс, 28 урок, Аксиома параллельных прямыхСкачать

   

   ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

   

   Геометрия 7 класс | Вертикальные, смежные, накрест лежащие и другие углы (теория) | МАТЕМАТИКА 2021Скачать

   

   SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать