Конспект урока
Свойства параллельных прямых
Перечень рассматриваемых вопросов:
- Углы, образованные при пересечении двух прямых секущей.
- Доказательство свойств параллельных прямых и их применение при решении задач.
- Формулирование теоремы об углах с соответственно параллельными сторонами.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Утверждение, обратное данной теореме– это утверждение, в котором условие является заключением теоремы, а заключение – условием теоремы.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее мы узнали и научились применять признаки параллельности прямых.
Рассмотрим утверждения, обратные к теоремам, выражающим признаки параллельности двух прямых.
В любой теореме есть две части: условие (это то, что дано)и заключение (это то, что требуется доказать).
Утверждением, обратным данному, называется утверждение, в котором условием является заключение, а заключением – условие.
Итак, вспомним один из признаков параллельности прямых. Если при пересечении двух прямых секущей накрест лежащие углы, образованные этими прямыми и секущей, равны (это условие), то прямые параллельны (заключение).
Сформулируем и докажем обратное утверждение.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы,образованные этими прямыми и секущей,равны.
∠1 и ∠2 – накрест лежащие.
Доказательство:( метод от противного):
Отложим ∠PMN =∠2 (накрест лежащие) → МР║b→ через точку М проходит 2 параллельные прямые прямой b (МР║b– доказательство;a║b– условие).→∠1=∠2.
Это противоречит теореме о единственности прямой параллельной данной и проходящей через точку.
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
С пересекает а, значит, и пересекает параллельную ей прямую b(по следствию из аксиомы параллельных прямых).→ с – секущая к прямым а и b→∠1 = ∠2 = 90° (по только что доказанному свойству параллельных прямых).→ с ┴ b.
Что и требовалось доказать.
Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей соответственные углы равны(это условие), то прямые параллельны(заключение).
Сформулируем и докажем обратное утверждение
Если две параллельные прямые пересечены секущей, то соответственные углы, образованные этими прямыми и секущей, равны.
Дано:
Доказать:
По условию a║b→∠1 = ∠3 (накрест лежащие углы). → ∠2 = ∠3 (вертикальные углы).
Значит, ∠1 = ∠2, что и требовалось доказать.
Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей сумма односторонних углов, образованных этими прямыми и секущей, равна 180° (условие), то прямые параллельны (заключение).
Сформулируем и докажем обратное утверждение.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов, образованных этими прямыми и секущей, равна 180°.
Дано:a║b,
Доказать:
По условию a║b→∠1=∠2 ‑соответственные углы, (в силу предыдущей теоремы).
∠2+∠4=180° (по свойству смежных углов).
→ ∠1+∠4= 180°,что и требовалось доказать.
Материал для углубленного изучения темы.
Задача на доказательство.
Прямая m пересекает параллельные прямые а и b в точках А и В. Прямая р, проходящая через середину отрезка АВ, точку О, пересекает прямые а и b в точках С и D.
Докажем, что ОС=ОD.
По условию дано: а ║b, рՈа= А, рՈb = В, mՈа = D, mՈb = C.
Доказать: ОС = ОD.
Доказательство: рассмотрим, образовавшиеся при построении, треугольники AOD и BOC. Они равны по 2 признаку равенства треугольников, т.к. АО=ВО (О– середина отрезка АВ по условию); ∠1=∠2(накрест лежащие углы); ∠3=∠4 (вертикальные углы). →Все элементы равных треугольников соответственно равны → ОС=ОD. Что и требовалось доказать.
Разбор заданий тренировочного модуля.
1. Три прямых а,р,с пересечены прямой k, при этом образуются соответственные углы: ∠1= 30°,∠2 = 40°,∠3= 30°,как показано на рисунке. Какие из прямых параллельны?
На рисунке изображены прямые а, р, с, которые пересечены секущей k. При этом углы 1,2,3 соответственные. По условию: ∠3= ∠1= 30°,∠2 ≠ ∠1,∠2 ≠ ∠3.
Следовательно, прямые а и р параллельные, прямые а и с, р и с не параллельные(по свойствам параллельных прямых).
2. На рисунке прямые а║b, при этомMO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ, если сумма углов в треугольнике равна 180°?
По условию а║b→∠М+∠Е=180° (по теореме о параллельных прямых об односторонних углах). Т.к. MO и ЕО – биссектрисы углов М и Е →∠М = 2∠ОМЕ,
∠М+∠Е =2∠ОМЕ +2∠МЕО =180°.
По условию сумма углов в треугольнике равна 180° → в ∆МОЕ.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Свойство углов образованных при пересечении параллельных прямых секущей доказательство
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Свойство углов, образованных при пересечении параллельных прямых секущей
Теорема 4.3 (обратная теореме 4.2). Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
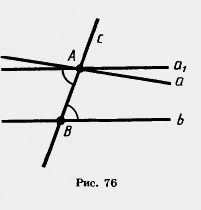
Доказательство. Пусть а и b — параллельные прямые и с — прямая, пересекающая их в точках А и В. Проведем через точку А прямую а1 так, чтобы внутренние накрест лежащие углы, образованные секущей с с прямыми а, и b, были равны (рис. 76).
По признаку параллельности прямых прямые а, и b параллельны. А так как через точку А проходит только одна прямая, параллельная прямой b, то прямая а совпадает с прямой а1.
Значит, внутренние накрест лежащие углы, образованные секущей с параллельными прямыми а и b, равны. Теорема доказана.
Из свойства углов, образованных при пересечении параллельных прямых секущей, следует, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
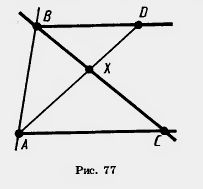
Задача (13). Прямые АС и BD параллельны, причем точки А и D лежат по разные стороны от секущей ВС (рис. 77). Докажите, что:
1) углы ВВС и АСВ внутренние накрест лежапще относительно секущей ВС;
2) луч ВС проходит между сторонами угла ABD;
3) углы CAB и DBA внутренние односторонние относительно секущей АВ.
1) Углы DBC и АСВ внутренние накрест лежащие потому, что точки А и D лежат по разные стороны от секущей ВС.
2) Луч ВС проходит между сторонами угла ABD потому, что он пересекает отрезок AD с концами на сторонах угла (задача 4).
3) Углы CAB и DBA внутренние односторонние потому, что точки С и D лежат по одну сторону от секущей АВ, а именно в полуплоскости, где лежит точка X пересечения отрезков ВС и AD.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Свойство углов образованных при пересечении параллельных прямых секущей доказательство
§ 15. Свойства параллельных прямых
(обратная теореме 14.1)
Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.
На рисунке 224 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.
Пусть ∠ 1 ≠ ∠ 2. Тогда через точку K проведём прямую a 1 так, чтобы ∠ 3 = ∠ 2 (рис. 224). Углы 3 и 2 являются накрест лежащими при прямых a 1 и b и секущей c . Тогда по теореме 14.1 a 1 ‖ b . Получили, что через точку K проходят две прямые, параллельные прямой b . Это противоречит аксиоме параллельности прямых. Таким образом, наше предположение неверно, и, следовательно, ∠ 1 = ∠ 2.
(обратная теореме 14.3)
Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.
На рисунке 225 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.
По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 равны как вертикальные. Следовательно, ∠ 1 = ∠ 2.
(обратная теореме 14.2)
Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180° .
На рисунке 226 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 + ∠ 2 = 180°.
По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 смежные, поэтому ∠ 1 + ∠ 3 = 180°. Следовательно, ∠ 1 + ∠ 2 = 180°.
Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой ( рис. 227 ).
Докажите это следствие самостоятельно.
Задача. Докажите, что все точки одной из двух параллельных прямых равноудалены от другой прямой.
Решение. Пусть прямые a и b параллельны (рис. 228), M и N — две произвольные точки прямой a . Опустим из них перпендикуляры MK и NP на прямую b . Докажем, что MK = NP .
Рассмотрим треугольники MKN и PNK . Отрезок KN — их общая сторона. Так как MK ⊥ b и NP ⊥ b , то MK ‖ NP , а углы MKN и PNK равны как накрест лежащие при параллельных прямых MK и NP и секущей KN .
Аналогично углы MNK и PKN равны как накрест лежащие при параллельных прямых MN и KP и секущей KN . Следовательно, треугольники MKN и PNK равны по стороне и двум прилежащим углам.
Тогда MK = NP .
Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.
Например, на рисунке 228 длина отрезка MK — это расстояние между параллельными прямыми a и b .
Задача. На рисунке 229 отрезок AK — биссектриса треугольника ABC , MK ‖ AC . Докажите, что треугольник AMK — равнобедренный.
Решение. Так как AK — биссектриса треугольника ABC , то ∠ MAK = ∠ KAC .
Углы KAC и MKA равны как накрест лежащие при параллельных прямых MK и AC и секущей AK . Следовательно, ∠ MAK = ∠ MKA .
Тогда треугольник AMK — равнобедренный.
- Каким свойством обладают накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей?
- Каким свойством обладают соответственные углы, образованные при пересечении двух параллельных прямых секущей?
- Чему равна сумма односторонних углов, образованных при пересечении двух параллельных прямых секущей?
- Известно, что прямая перпендикулярна одной из двух параллельных прямых. Обязательно ли она перпендикулярна другой прямой?
- Что называют расстоянием между двумя параллельными прямыми?
326. На рисунке 230 найдите угол 1.
327. На рисунке 231 найдите угол 2.
328. Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.
329. Один из односторонних углов, образованных при пересечении двух параллельных прямых секущей, в 4 раза больше другого. Найдите эти углы.
330. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если:
1) один из этих углов равен 48°;
2) отношение градусных мер двух из этих углов равно 2 : 7.
331. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них на 24° меньше другого.
332. На рисунке 232 m ‖ n , p ‖ k , ∠1 = 50°. Найдите ∠ 2, ∠ 3 и ∠ 4.
333. Прямая, параллельная основанию AC равнобедренного треугольника ABC , пересекает его боковые стороны AB и BC в точках D и F соответственно. Докажите, что треугольник DBF — равнобедренный.
334. На продолжениях сторон AC и BC треугольника ABC ( AB = BC ) за точки A и B отметили соответственно точки P и K так, что PK ‖ AB . Докажите, что треугольник KPC — равнобедренный.
335. Отрезки AB и CD пересекаются в точке O , AO = BO , AC ‖ BD . Докажите, что CO = DO .
336. Отрезки MK и DE пересекаются в точке F , DK ‖ ME , DK = ME . Докажите, что ∆ MEF = ∆ DKF .
337. Ответьте на вопросы.
1) Могут ли оба односторонних угла при двух параллельных прямых и секущей быть тупыми?
2) Может ли сумма накрест лежащих углов при двух параллельных прямых и секущей быть равной 180°?
3) Могут ли быть равными односторонние углы при двух параллельных прямых и секущей?
338. На рисунке 233 AB ‖ CD , BC ‖ AD . Докажите, что BC = AD .
339. На рисунке 233 BC = AD , BC ‖ AD . Докажите, что AB ‖ CD .
340. На рисунке 234 MK ‖ EF , ME = EF , ∠ KMF = 70°. Найдите ∠ MEF .
341. Через вершину B треугольника ABC (рис. 235) провели прямую MK , параллельную прямой AC , ∠ MBA = 42°, ∠ CBK = 56°. Найдите углы треугольника ABC .
342. Прямая, проведённая через вершину A треугольника ABC параллельно его противолежащей стороне, образует со стороной AC угол, равный углу BAC . Докажите, что данный треугольник — равнобедренный.
343. На рисунке 236 ∠ MAB = 50°, ∠ ABK = 130°, ∠ ACB = 40°, CE — биссектриса угла ACD . Найдите углы треугольника ACE .
344. На рисунке 237 BE ⊥ AK , CF ⊥ AK , CK — биссектриса угла FCD , ∠ ABE = 32°. Найдите ∠ ACK .
345. На рисунке 238 BC ‖ MK , BK = KE , CK = KD . Докажите, что AD ‖ MK .
346. На рисунке 239 AB = AC , AF = FE , AB ‖ EF . Докажите, что AE ⊥ BC .
347. Треугольник ABC — равнобедренный с основанием AC . Через произвольную точку M его биссектрисы BD проведены прямые, параллельные его сторонам AB и BC и пересекающие отрезок AC в точках E и F соответственно. Докажите, что DE = DF .
348. На рисунке 240 AB ‖ DE . Докажите, что ∠ BCD = ∠ ABC + ∠ CDE .
349. На рисунке 241 AB ‖ DE , ∠ ABC = 120°, ∠ CDE = 150°. Докажите, что BC ⊥ CD .
350. Через вершину B треугольника ABC провели прямую, параллельную его биссектрисе AM . Эта прямая пересекает прямую AC в точке K . Докажите, что ∆ BAK — равнобедренный.
351. Через точку O пересечения биссектрис AE и CF треугольника ABC провели прямую, параллельную прямой AC . Эта прямая пересекает сторону AB в точке M , а сторону BC — в точке K . Докажите, что MK = AM + CK .
352. Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O . Через эту точку проведены прямые, параллельные прямым AB и BC и пересекающие сторону AC в точках M и K соответственно. Докажите, что периметр треугольника MOK равен длине стороны AC .
Упражнения для повторения
353. На отрезке AB отметили точку C так, что AC : BC = 2 : 1. На отрезке AC отметили точку D так, что AD : CD = 3 : 2. В каком отношении точка D делит отрезок AB ?
354. Отрезки AC и BD пересекаются в точке O , AB = BC = CD = AD . Докажите, что AC ⊥ BD .
355. В треугольнике MOE на стороне MO отметили точку A , в треугольнике TPK на стороне TP — точку B так, что MA = TB . Какова градусная мера угла BKP , если MO = TP , ∠ M = ∠ T , ∠ O = ∠ P , ∠ AEO = 17°?
Наблюдайте, рисуйте, конструируйте, фантазируйте
356. На рисунке 242 изображена очень сложная замкнутая ломаная. Она ограничивает некоторую часть плоскости (многоугольник). Как, отметив на рисунке любую точку, по возможности быстрее определить, принадлежит эта точка многоугольнику или нет?
🔥 Видео
Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать

ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

Углы, образованные при пересечении двух прямых секущейСкачать

СВОЙСТВО УГЛОВ, ОБРАЗОВАННЫХ ПРИ ПЕРЕСЕЧЕНИИ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ СЕКУЩЕЙСкачать

Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

7 класс. Геометрия. Урок 13. Свойства углов при пересечении параллельных прямых секущей: теорияСкачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

УГЛЫ: Односторонние, Накрест Лежащие, Внутренние, Внешние // Теорема об углах — Геометрия 7 классСкачать

Теорема 14.2 Если сумма односторонних углов равна 180 градусов, то прямые параллельны || Геометрия 7Скачать

Геометрия 7 класс. Теоремы об углах, образованных двумя параллельными прямымСкачать

Углы, образованные параллельными прямыми и секущейСкачать