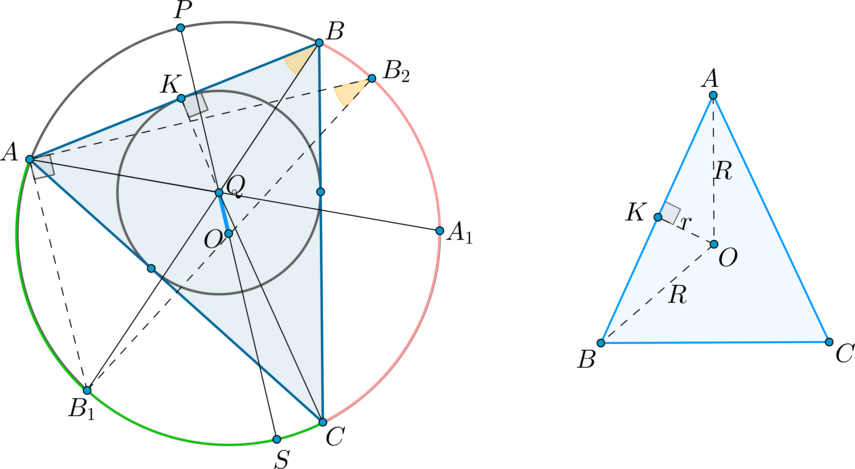
В треугольнике OI 2 =R 2 -2Rr , где I — точка пересечения биссектрис (центр вписанной окружности), O — центр описанной окружности, R — радиус описанной окружности, r — радиус вписанной окружности.
Доказательство:
Пусть AM — хорда описанной окружности, проходящая через точку I.
Тогда по теореме о пересекающихся хордах: AI·IM=(R+OI)(R-OI).
Из треугольника AIH по определению синуса: AI=r/sin(α/2).
Из треугольника MAC по теореме синусов и лемме о трезубце: CM=2Rsin(α/2)=IM.
Подставим полученные равенства в AI·IM=(R+OI)(R-OI):
r/sin(α/2)·2Rsin(α/2)= R 2 -OI 2
Следовательно, OI 2 =R 2 -2Rr.
- Как найти расстояние между центрами окружностей
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Ответ
- Проверено экспертом
- Основные теоремы, связанные с окружностями
- 📽️ Видео
Видео:Расстояние между центрами. Окружность. Математика 10-11 классы.Скачать

Как найти расстояние между центрами окружностей
У Вас недостаточно прав для добавления комментариев.
Вам необходимо зарегистрироваться на сайте
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям | |
 | |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
| Фигура | Рисунок | Формула | ||
| Внешняя касательная к двум окружностям |  | |||
| Внутренняя касательная к двум окружностям |  | |||
| Общая хорда двух пересекающихся окружностей |  | |||
| Внешняя касательная к двум окружностям | |
 | |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
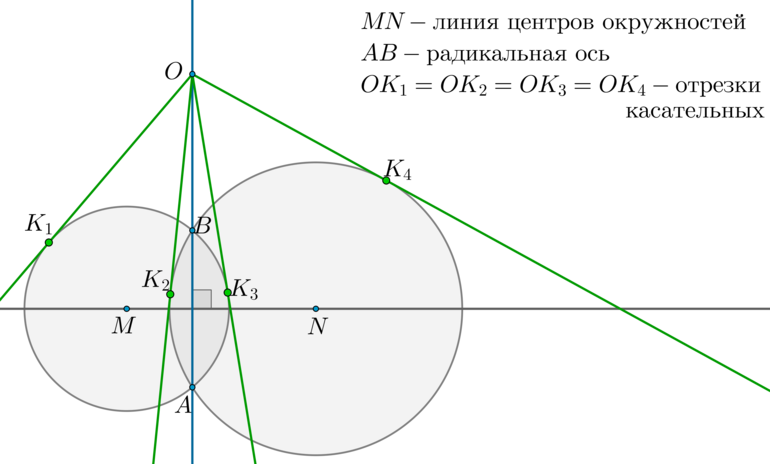
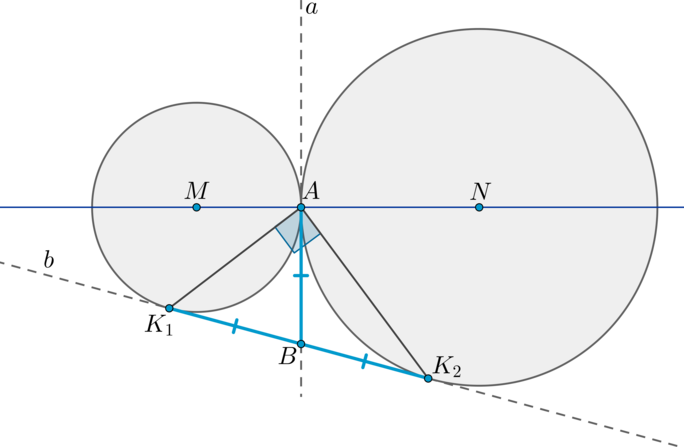
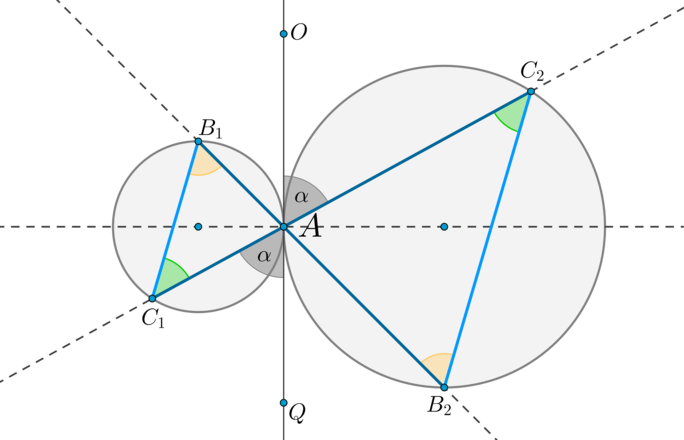
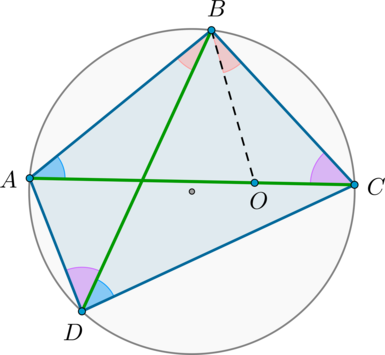
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать  ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать  Основные теоремы, связанные с окружностямиРадикальная ось — прямая, проходящая через точки пересечения двух окружностей. Теорема 1. 1) Радикальная ось перпендикулярна линии центров окружностей. Доказательство: 1) Рассмотрим (triangle BMN) и (triangle AMN) : они равны по трем сторонам ( (BM=AM=R_1, BN=AN=R_2) — радиусы первой и второй окружностей соответственно). Таким образом, (angle BNM=angle ANM) , следовательно, (MN) — биссектриса в равнобедренном (triangle ANB) , следовательно, (MNperp AB) . 2) Отметим произвольную точку (O) на радикальной оси и проведем касательные (OK_1, OK_3) к первой окружности и (OK_2, OK_4) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то (OK_1^2=OK_2^2=OK_3^2=OK_4^2=OBcdot OA) . Теорема 2. Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A) . Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B) . Точки касания — точки (A, K_1, K_2) (как показано на рисунке). Тогда [(1) <large>] [(2) <large>] Доказательство: 1) Т.к. (BA) и (BK_1) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: (BA=BK_1) . Аналогично, (BA=BK_2) . Таким образом, (BA=BK_1=BK_2) . 2) Значит, (BA) — медиана в (triangle K_1AK_2) , равная половине стороны, к которой она проведена. Значит, (angle A=90^circ) . Теорема 3. Пусть две окружности касаются внешним образом в точке (A) . Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2) , пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [(1) <large>] [(2) <large>] Доказательство: 1) Проведем через точку (A) общую касательную этих окружностей (OQ) . (angle OAC_2=angle QAC_1=alpha) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то (angle OAC_2=frac12buildrelsmileover) , (angle QAC_1=frac12buildrelsmileover) . Следовательно, (buildrelsmileover=buildrelsmileover=2alpha) . Таким образом, (angle AB_1C_1=angle AB_2C_2=alpha) . Значит, по двум углам (triangle AB_1C_1sim triangle AB_2C_2) . 2) Т.к. (angle AB_1C_1=angle AB_2C_2) , то прямые (B_1C_1parallel B_2C_2) по накрест лежащим углам при секущей (B_1B_2) . Теорема Птолемея Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: [ACcdot BD=ABcdot CD+BCcdot AD] Доказательство Пусть для определенности (angle ABD . Проведем отрезок (BO) так, чтобы (O) лежала на (AC) и (angle ABD=angle CBO) : Т.к. (angle ACB=angle ADB) (опираются на одну и ту же дугу), то по двум углам (triangle OBCsim triangle ABD) . Значит: [dfrac=dfrac Rightarrow ADcdot BC=OCcdot BDphantom (1)] Т.к. (angle BAC=angle BDC) (опираются на одну и ту же дугу), (angle ABO=angle CBD) (состоят из равных по построению (оранжевых) углов и общего угла (angle DBO) ), то по двум углам (triangle ABOsim triangle BDC) . Значит: [dfrac=dfrac Rightarrow ABcdot CD=AOcdot BD phantom (2)] Сложим равенства ((1)) и ((2)) : (ADcdot BC+ABcdot CD=OCcdot BD+AOcdot BD=ACcdot BD) , чтд. Формула Эйлера: Пусть (R) — радиус описанной около треугольника (ABC) окружности, (r) — радиус вписанной окружности. Тогда расстояние (d) между центрами этих окружностей вычисляется по формуле: [<large>] Доказательство: а) Предположим, что (dne 0) . Пусть (O, Q) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности (PS) через точку (Q) . Проведем также биссектрисы углов (angle A, angle B) — (AA_1, BB_1) соответственно (заметим, что они пересекутся в точке (Q) , т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды (PS) и (BB_1) пересекаются, следовательно, отрезки этих хорд равны: (PQcdot QS=BQcdot QB_1) . Т.к. (OP=OS=R, OQ=d) , то последнее равенство можно переписать в виде ((R-d)(R+d)=BQcdot QB_1 (*)) . Заметим, что т.к. (AA_1, BB_1) — биссектрисы, то (buildrelsmileover=buildrelsmileover=x, buildrelsmileover=buildrelsmileover=y) . Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то: С другой стороны, (angle B_1AA_1=frac12big(buildrelsmileover+buildrelsmileoverbig)=frac12(x+y)) Таким образом, (angle AQB_1=angle B_1AA_1) . Следовательно, (triangle QB_1A) — равнобедренный и (B_1Q=B_1A) . Значит, равенство ((*)) можно переписать как: Проведем еще один диаметр описанной окружности (B_1B_2) . Тогда (triangle B_1AB_2) — прямоугольный ( (angle A) опирается на диаметр). Пусть также вписанная окружность касается стороны (AB) в точке (K) . Тогда (triangle BKQ) — прямоугольный. (dfrac=dfrac Rightarrow dfrac=dfrac Rightarrow BQcdot AB_1=2Rr) . Подставим это в ((**)) и получим: (R^2-d^2=2Rr Rightarrow d^2=R^2-2Rr) . б) Если (d=0) , т.е. центры вписанной и описанной окружностей совпадают, то (AK=BK=sqrt Rightarrow AB=2sqrt) . Аналогично (AC=BC=AB=sqrt) , т.е. треугольник равносторонний. Следовательно, (angle A=60^circ Rightarrow angle KAO=30^circ Rightarrow r=frac12R Rightarrow R=2r) или (0=R^2-2Rr) (т.е. в этом случае формула также верна). Теорема о бабочке: Пусть через середину хорды (AB) — точку (O) , проведены две хорды (MN) и (KP) . Пусть (MPcap AB=X, KNcap AB=Y) . Тогда [<large>] Доказательство: Проведем перпендикуляры (XX_1, YY_2perp MN, XX_2, YY_1perp KP) . Следующие прямоугольные треугольники подобны: 1) (triangle XX_1Osim triangle YY_2O Rightarrow dfrac=dfrac) 2) (triangle XX_2Osim triangle YY_1O Rightarrow dfrac=dfrac) 3) (triangle MXX_1sim triangle KYY_1 Rightarrow dfrac=dfrac) 4) (triangle PXX_2sim triangle NYY_2 Rightarrow dfrac=dfrac) Из 1) и 2) следует, что Из 3) и 4) следует, что Совместив последние два равенства, получим: Заметим, что для пересекающихся хорд (AB) и (MP) : (AXcdot XB=MXcdot PX) . Аналогично (AYcdot YB=KYcdot NY) . Значит: Обозначим (OX=x, OY=y, OA=OB=t Rightarrow) 📽️ Видео#234. Формула Эйлера | Свойства отрезков хорд и секущихСкачать  Как найти расстояние между центрами | Олимпиадная математикаСкачать  М1152. Расстояние между центрами вписанной и описанной окружностейСкачать  7 9 2011 М1152 формула Эйлера расстояния между центрами вписанной и описанной окружностейСкачать  Уравнение окружности и формула расстояния между точками на плоскостиСкачать  12.7 - Формула Эйлера расстояния между центрами...Скачать  Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать  Деление окружности на 3; 6; 12 равных частейСкачать  Длина отрезкаСкачать  Сможешь найти расстояние между центрами пересекающихся окружностей?Скачать 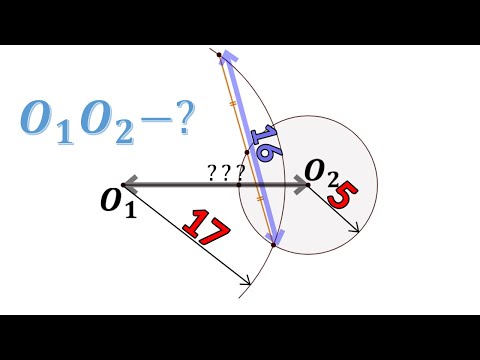 расстояние между центрамиСкачать  ЕГЭ и ОГЭ. Окружности и касательные, секущие, подобие. Свойства. Расстояние между центрами.Скачать  1 2 4 сопряжение окружностейСкачать  Уравнение окружности (1)Скачать  |